Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
1.5. Обратное z-преобразование
Обратным называется преобразование, позволяющее определять оригинал функции f[n] по заданному изображению F(z). Символически обратное преобразование Лорана записывается следующим образом:
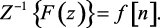(1.80)
Метод вычетов. Для вывода формулы обратного преобразования умножим обе части уравнения для прямого преобразования (1.46) на
zm–1dz [68]:
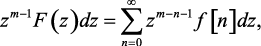(1.81)
где m – целое число.
Напомним, что ряд (1.46) сходится вне круга радиуса R0. Следовательно, вне круга R0 функция F(z) не должна иметь полюсов, так как иначе в полюсе zi она приняла бы значение бесконечности, и ряд был бы расходящимся. Поэтому все полюсы функции F(z), если они существуют, должны находиться во внутренней области, ограниченной кругом радиуса R0 с центром в начале координат.
Возьмем интеграл по окружности R0 от левой и правой частей соотношения (1.81)
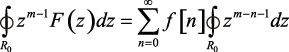(1.82)
Если n < m, то число m – n – 1 ≥ 0 и подынтегральная функция в правой части уравнения (1.82) регулярна во всей области комплексного z, вследствие чего согласно теореме Коши
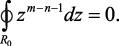(1.83)
При n > m число m – n – 1 = –k < –1 и
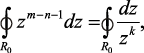(1.84)
где k > 1.
Подынтегральная функция f(z) = 1/zk имеет полюс k-го порядка в начале координат. Значение интеграла этой функции согласно теореме Коши о вычетах будет иметь вид:
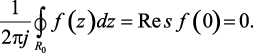(1.85)
Таким образом, при n > m
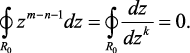(1.86)
Остается только значение n = m, при котором интеграл в правой части уравнения (1.82) не равен нулю. В этом интеграле
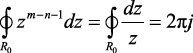. (1.87)
Учитывая изложенное, можно записать
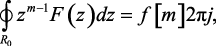(1.88)
откуда
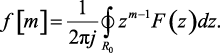(1.89)
Заменяя m на n, получим формулу для обратного преобразования Лорана
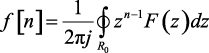(1.90)
или
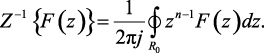(1.90а)
Согласно теореме Коши о вычетах, правая часть соотношения (1.90) равна сумме вычетов подынтегральной функции внутри круга радиуса R0
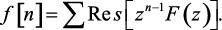(1.91)
Пример 1.7. Для конденсаторного счетчика импульсов, переходный процесс в котором описывается разностным уравнением (1.38)
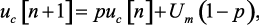
найти точное решение в виде математического выражения.
Решение. Перепишем уравнение (1.38) в виде
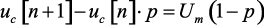(1.92)
и применим к нему преобразование Лорана
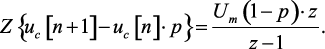(1.93)
Полагая uc[0] = 0, получим изображение напряжения на конденсаторе
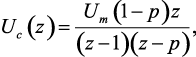(1.94)
для которого оригинал
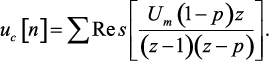(1.95)
Поскольку функция (1.94) имеет два полюса z1 = 1 и z1 = p, то окончательное выражение оригинала имеет следующий вид
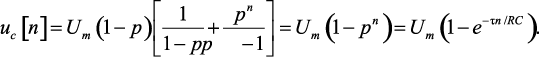(1.96)
Выражение (1.96) совпадает с полученным ранее выражением (1.41).
Метод разложения в ряд. Практическое применение формулы обратного преобразования связано с громоздким вычислением полюсов функции F(z). Поэтому для нахождения решетчатых функций по их z-преобразованиям применяются некоторые другие методы. В частности, если функция F(z) является дробно-рациональной, то есть
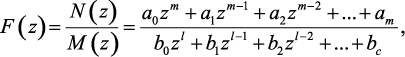(1.97)
то весьма удобно вычислять решетчатую функцию f[n], разложив F(z) в ряд Лорана
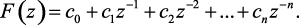(1.98)
С другой стороны, из основной формулы (1.46) прямого z-преобразования решетчатой функции следует
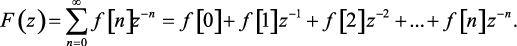(1.99)
Сравнение двух рядов (1.98) и (1.99) позволяет сделать следующий вывод:
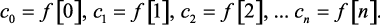(1.100)
Таким образом, разложив каким-либо способом функцию F(z) в ряд Лорана по убывающим степеням z и вычислив коэффициенты этого ряда, можно непосредственно определить значения решетчатой функции f[n] в дискретных точках, не прибегая к операциям нахождения полюсов функции F(z).
Разностное уравнение. Если известно изображение выходного сигнала устройства в виде
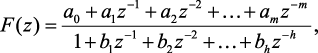(1.101)
для определения оригинала f[n] может быть использована рекуррентная формула [95], которая следует из алгоритма деления числителя N(z) на знаменатель M(z) функции F(z)
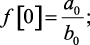(1.102а)
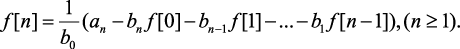(1.102б)
Если n > 1 и n > m, то в этой формуле все bi при i > h и an отсутствуют, и формула (1.102б) примет следующий вид:
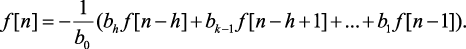(1.103)
Если известна импульсная передаточная функция устройства
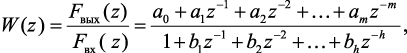(1.104)
то для нахождения отклика fвых[n] на входное воздействие fвх[n – k] в тактовые моменты времени может быть использовано разностное уравнение
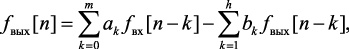(1.105)
коэффициенты которого определяются непосредственно по уравне-
нию (1.104) без дополнительных вычислительных операций.
Выражение (1.102) и (1.103) позволяют, не производя непосредственное деление, определять дискретные значения функции-оригинала рекуррентным методом. С помощью компьютера эта задача решается довольно легко. Причем, вычисления по формулам (1.102) целесообразно выполнить предварительно вручную, так как число значений функции f[n], вычисляемых по формуле (1.102), равно наивысшей степени полинома M(z), а вычисления по формуле (1.103) уже производить с помощью компьютера.