
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
1.9. Операторно-дискретный метод. Основные законы электрических цепей в операторно-дискретной форме
Для моделирования динамических процессов в электрических цепях и системах разработан операторно-рекуррентный метод анализа, который основан на z-преобразовании [95]. При применении этого метода непрерывные модели предварительно с помощью операции дискретизации искусственно приводятся к дискретным моделям, затем осуществляется z-преобразование. В области изображений выполняются математические преобразования и анализ, а затем осуществляется переход к временным функциям. Однако в этом методе в качестве исходной информации для определения изображений используются математические уравнения. В тоже время основной математической моделью электромеханических и электронных устройств являются их схемы замещения. Поэтому для удобства моделирования электрических схем разработан операторно-дискретный метод, позволяющий получить разностные уравнения непосредственно по электрической схеме с нулевыми и ненулевыми начальными условиями [88]. Основываясь на схемах замещения, такой подход позволяет единообразно формализовать различные электрические и электромеханические задачи, и на основе построенных моделей произвести численное моделирование для заданного входного воздействия. Предлагаемый метод основан на том, что непрерывная система искусственно приводится к дискретной, и дискретизация осуществляется на начальном этапе решения задачи, что позволяет без составления исходных математических выражений получать разностные уравнения непосредственно по электрическим схемам замещения [94]. Рассмотрим методику получения дискретной схемы замещения на примере схемы, изображенной на рис. 1.16.
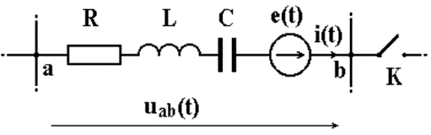
Рис. 1.16. Ветвь электрической цепи, содержащая
R, L, С-элементы, источник e(t)
Закон Ома. Рассмотрим ветвь электрической цепи, содержащую активный R, индуктивный L, емкостный С элементы и источник ЭДС e(t) (рис. 1.16) [88]. Замыкание ключа К приводит к переходному процессу в электрической схеме, определим реакцию на единичное ступенчатое воздействие. До коммутации ток в цепи равен i = i(0), а напряжение на конденсаторе uc = uc(0). Ток в ветви, который является реакцией на воздействие 1(t), обозначим – i(t).
Напряжение между узлами а и b определяется выражением
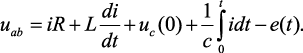 (1.128)
(1.128)
Для возможности применения дискретных преобразований в анализе и расчете участка электрической цепи преобразуем непрерывные функции i(t), e[n] в дискретные i[n], e[n] путем введения в ветвь фиктивного ключа, то есть, осуществим теоретическую дискретизацию непрерывных функций. Введение же реального ключа приведет к значительному изменению токов и напряжений в схеме. Очевидно, что дискретной функцией будет ток и напряжение между узлами а и b – uab[n]. К уравне-
нию (1.128) применим преобразование Лорана. Преобразование Лорана является линейным, поэтому изображение суммы равно сумме изображений. Введем следующие обозначения
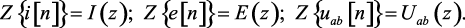 (1.129)
(1.129)
Изображение от постоянной величины uc(0) определяется с помощью теоремы (1.52)
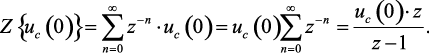 (1.130)
(1.130)
При дискретизации непрерывной функции i(t) ее производная заменяется конечной разностью решетчатой функции
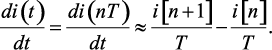 (1.131)
(1.131)
Используя теорему запаздывания (сдвига) определим преобразование Лорана от конечной разности (1.131)
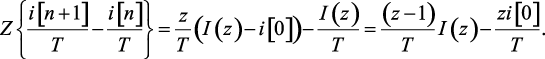 (1.132)
(1.132)
При определении изображения производной можно также использовать обратную разность
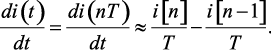 (1.133)
(1.133)
Для определения изображения конечной разности (1.133) используем теорему запаздывания. При m < 0 математическое выражение (1.53) упрощается, так как член 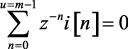 поскольку i[n] = 0 при n < 0, и имеет вид
поскольку i[n] = 0 при n < 0, и имеет вид
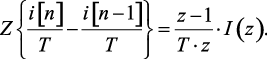 (1.134)
(1.134)
Во втором варианте определения изображения конечной разнос-
ти (1.134) потеряна информация о начальных условиях и поэтому выражение может быть использовано в задачах с нулевыми начальными условиями. Изображение функции i[n] в выражениях (1.132) и (1.134) отличаются в z–1 раз, соответствует сдвигу оригиналов этой функции на один шаг.
При дискретизации интеграл в выражении (1.128) заменяется суммой
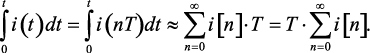 (1.135)
(1.135)
Определим преобразование Лорана от суммы (1.135)
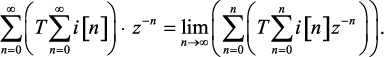 (1.136)
(1.136)
Выражение, от которого определяется предел (1.136), можно представить в виде следующего ряда
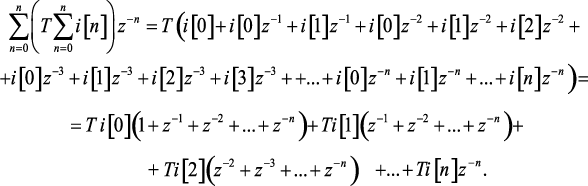 (1.137)
(1.137)
Сумма членов в первой скобке выражения (1.137) представляет собой сумму членов геометрической прогрессии, начиная с нулевого члена и поэтому ее можно представить в виде конечного выражения
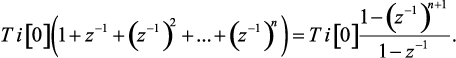 (1.138)
(1.138)
Суммы членов в каждой последующей скобке выражения (1.137) можно представить как разности сумм членов геометрических прогрессий, начинающихся с нулевых членов, и следовательно эти суммы выразить в следующем виде:
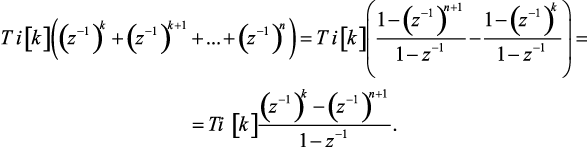 (1.139)
(1.139)
Подставляя в выражение (1.137) значения сумм (1.138) и (1.139), обозначенных скобками, получим более компактное выражение сумм
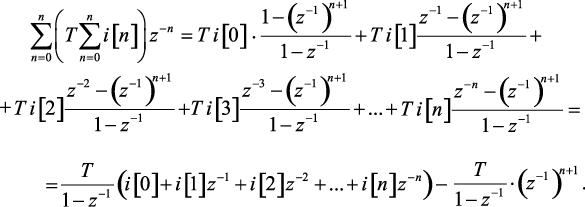 (1.140)
(1.140)
Далее определим изображение суммы, то есть предел выраже-
ния (1.140) при n → ∞
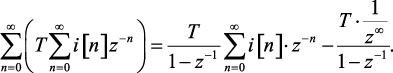 (1.141)
(1.141)
Поскольку по определению 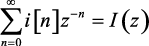 , а по условию сходимости ряда
, а по условию сходимости ряда 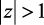 , то выражение (1.141) несколько упростится
, то выражение (1.141) несколько упростится
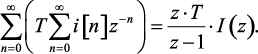 (1.142)
(1.142)
Определив преобразования Лорана от всех членов выражения (1.128) с помощью полученных выше соотношений (1.130), (1.132) и (1.142), получим выражение для изображения напряжения между узлами а и b.
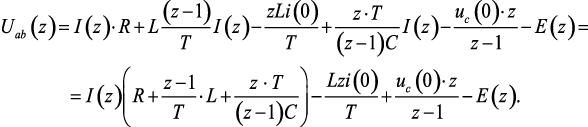 (1.143)
(1.143)
Таким образом, вместо дифференциального уравнения (1.118) получили алгебраическое уравнение, связывающее изображение тока I(z) с изображениями ЭДС E(z) и напряжения Uab(z). Из уравнения (1.143) определяется выражение для тока, представляющее собой закон Ома в операторно-дискретной форме:
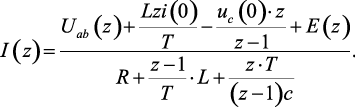 (1.144)
(1.144)
Введя обозначения членов в выражении (1.144), закон Ома представим в более компактном виде:
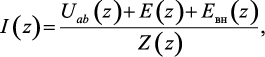 (1.145)
(1.145)
где 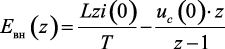 – изображение внутренних источников ЭДС, введение которых обусловлено запасом энергии в реактивных элементах цепи;
– изображение внутренних источников ЭДС, введение которых обусловлено запасом энергии в реактивных элементах цепи; 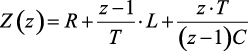 – операторно-дискретное сопротивление ветви.
– операторно-дискретное сопротивление ветви.
В частных случаях в формуле (1.144) могут отсутствовать какие-либо члены, так например запись закона Ома для участка цепи с нулевыми начальными условиями, не содержащего ЭДС имеет вид:
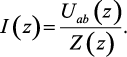 (1.146)
(1.146)
В соответствии с формулой (1.143) на рис. 1.17 изображена схема замещения участка цепи.
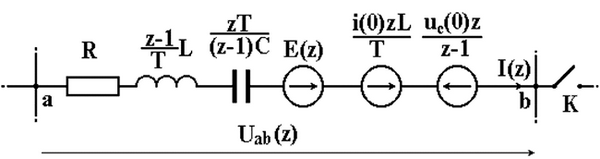
Рис. 1.17. Дискретная схема замещения ветви
Законы Кирхгофа
Первый закон Кирхгофа: алгебраическая сумма токов, протекающих к любому узлу цепи, равна нулю. В более общей форме закон формулируется следующим образом: алгебраическая сумма токов, протекающих сквозь любое сечение цепи, равна нулю. При этом сечением называется произвольная совокупность ветвей, при отсечении которых цепь распадается на две части.
Для сечения части электрической схемы, изображенной на рис. 1.18, уравнение, согласно первому закону Кирхгофа, будет иметь вид
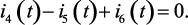 (1.147)
(1.147)
Применяя преобразование Лорана к уравнению (1.147), предварительно преобразовав непрерывные функции в дискретные, получим выражение первого закона Кирхгофа в операторно-дискретной форме
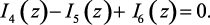 (1.148)
(1.148)
Второй закон Кирхгофа: алгебраическая сумма направленных падений напряжений вдоль любого замкнутого контура цепи равна нулю.
Для контура, изображенного на рис. 1.18, уравнение согласно второму закону Кирхгофа будет иметь вид:
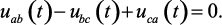 (1.149)
(1.149)
Применяя преобразование Лорана к уравнению (1.149), предварительно преобразовав непрерывные функции в дискретные, получим уравнение второго закона Кирхгофа в операторно-дискретной форме
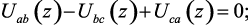 (1.150)
(1.150)
где 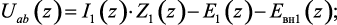
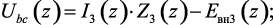
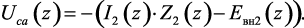
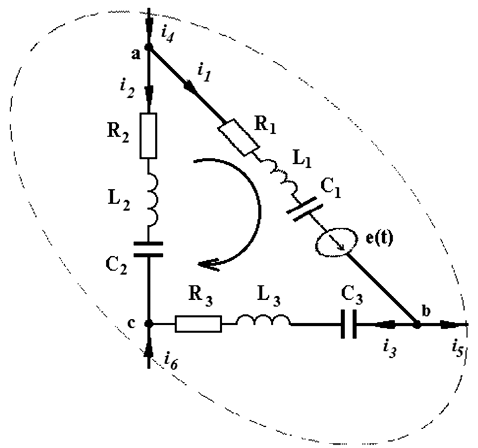
Рис. 1.18. Участок электрической схемы
Подставляя выражения для падений напряжений ветвей схемы в уравнение (1.150) получим уравнение второго закона Кирхгофа в виде
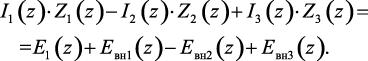 (1.151)
(1.151)
