Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
2.1. Конформные отображения областей устойчивости при моделировании аналоговых систем с помощью метода z-форм
При моделировании с использованием различных z-форм основным вопросом является устойчивость численной модели, поэтому целесообразно определить, каким образом область устойчивости из p-плоскости переходит в z-плоскость. Проведем анализ конформного отображения p-плоскости в z-плоскость в полярной системе координат, поскольку устойчивость характеризуется разностью между модулем 
и радиусом единичной окружности. Известно, что при стремлении периода дискретизации Т к нулю модуль 
стремиться к единице, поэтому аналитическое представление в полярной системе координат позволяет получить выражение скорости приближения модуля z-полюсов к границе устойчивости при уменьшении периода дискретизации (T → 0). Кроме того, в источнике [43] приводится оценка искажений частотных характеристик в цифровой форме. Эта оценка осуществляется визуально по неравномерности частотных сеток в z-плоскости. Исследование в полярной системе координат позволяет аналитически определить частотные искажения для различных методов аппроксимации. Кроме широко используемых методов аппроксимации первого порядка, таких как прямая разность, обратная разность и метод трапеций, рассмотрим метод интегрального преобразования без потерь [43]. Этот метод рекомендован для моделирования цифровых фильтров, работающих в колебательном режиме.
Рассмотрим соответствие между р и z-плоскостями при точном преобразовании z = epT и при использовании различных методов аппроксимации [77]. Преобразование плоскости, осуществляемое аналитической функцией z = f(p), обладает следующим важным свойством в окрестности точки р, для которой z′ ≠ 0. Бесконечно малые векторы всех направлений, выходящие из этой точки увеличиваются (или уменьшаются) по своей длине в одно и то же число раз, равное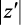 
и поворачиваются на один и тот же угол, равный arg z′. Таким образом, фигуры в бесконечно малой области преобразуются в себе подобные, то есть сохраняют форму. Такое преобразование является конформным отображением. Фигуры конечных размеров искажаются, но углы между двумя кривыми сохраняются. Таким образом, с помощью аналитических функций можно получить множество прямоугольных систем криволинейных координат. Обратно, для любого конформного отображения существует некоторая ортогональная сетка кривых, которая преобразуется в прямоугольную декартову сетку [11, 60].
Известно, что при дискретизации непрерывной функции с ограниченным спектром (ωс – высшая гармоническая составляющая сигнала или частота среза) p-плоскость делится на бесконечное число полос [37]. Определим предельные соотношения для основной полосы в области p-полюсов.
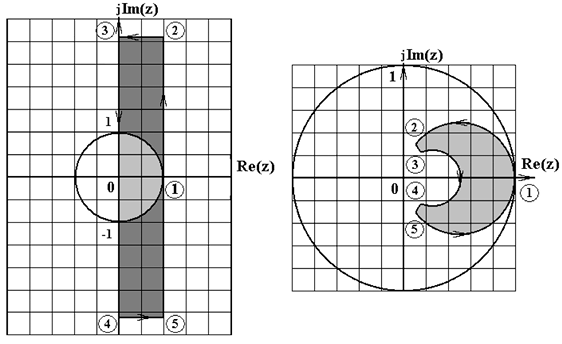
Пусть переменная в p-плоскости имеет выражение p = α + jω, и поскольку для устойчивой системы α < 0, рассмотрим левую полуплоскость (рис. 2.1, а). Частота ωд и период T дискретизации определяются с помощью теоремы Котельникова, а именно ωд = 2ωC или T = π/ωC. Поэтому основная полоса расположена в диапазоне частот от от –π/T до π/T. Область p-полюсов отображается преобразованием z = epT в круг с центром в начале координат и единичным радиусом, как показано на рис. 2.1, б [37]. Точки правой половины p-плоскости отображаются в область вне окружности единичного радиуса на z-плоскости. Эта область будет областью неустойчивости. При неограниченном увеличении затухания (α → –∞) устойчивая область полюсов преобразуется в единичный круг. Так как период дискретизации T гораздо меньше постоянной времени затухания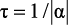 
, то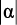 
не может быть больше 1/T. Поэтому область полюсов на p-плоскости ограничим прямыми α = 0, α = –1/T, ω = ±π/T (рис. 2.1, а). В этом случае прямая α = –1/T преобразуется в окружность с радиусом e–1 на z-плоскость.
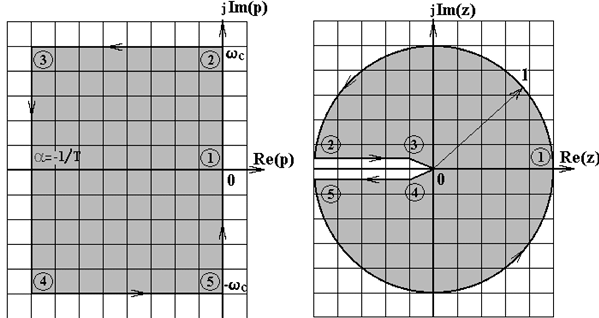
а б
Рис. 2.1. Конформное отображение области устойчивости p-плоскости
на z-плоскость, осуществляемое функцией z = epT
Проводя исследование преобразования p-плоскости на z-плоскость с помощью различных видов аппроксимации, введем безразмерные величины приведенного коэффициента затухания и приведенной частоты соответственно:
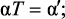(2.1)
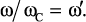(2.2)
При этом α′ принадлежит интервалу [–1; o], а ω′ – [–1; 1]. Представление любой величины в относительных единицах существенно упрощает теоретические выкладки и придает результатам бóльшую наглядность.
Рассмотрим уравнения конформных преобразований областей устойчивости с помощью z-форм.
Метод прямой разности. Используя формулу перехода p = (z – 1)/T выразим z-переменную через p-переменную
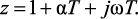(2.3)
Пусть z = x + jy, тогда из формулы (2.3) с учетом новых обозначений (2.1), (2.2) следует:
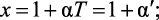
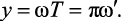(2.4)
Найдем модуль и аргумент z:
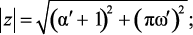(2.5а)
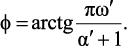(2.5б)
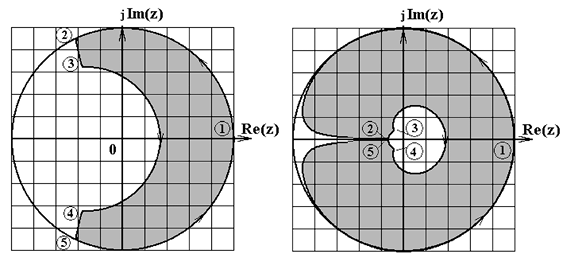
Конформное отображение области p-полюсов на z-плоскость в полярных координатах представлено на рис. 2.2, а.
Из анализа конформных отображений (рис. 2.2, а) следует, что p-область по методу прямой разности преобразуется в прямоугольник, который выходит за пределы единичного круга. Следовательно, при некоторых параметрах численной модели возможно неустойчивое решение. При преобразовании прямые линии, параллельные осям координат, в p-плоскости переходят в прямые линии на z-плоскости.
Поскольку при применении метода прямой разности может возникнуть неустойчивое решение, то необходимо определить ограничения на выбор параметров численной модели. Для этого с помощью метода прямой разности проведено обратное отображение области устойчивости z-плоскости на p-плоскость. (рис. 2.3) [76].
Окружность единичного радиуса преобразуется в окружность радиуса 1/T с центром в точке (–1/T; 0) (на рис. 2.3 задано T = 0,001). Если полюса системы окажутся внутри этой окружности, то численное решение при применении данной аппроксимации будет устойчиво. Если же хотя бы один из полюсов находится вне окружности радиуса 1/T, то при конформном отображении он не попадет в область единичного круга на z-плоскости (область устойчивости), а значит необходимо, либо уменьшить период дискретизации, что приведет к расширению области устойчивости, либо применить другую аппроксимацию.
а б
в г
Рис. 2.2. Конформные отображения области устойчивости
p-плоскости на z-плоскость с помощью методов:
а – прямой разности; б – обратной разности; в – Тустена;
г – преобразования без потерь
Условие выбора периода дискретизации для полюса, при котором система остаётся устойчивой, то есть, когда полюса системы находятся внутри окружности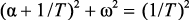 
, при применении прямой разности:
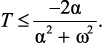(2.6)
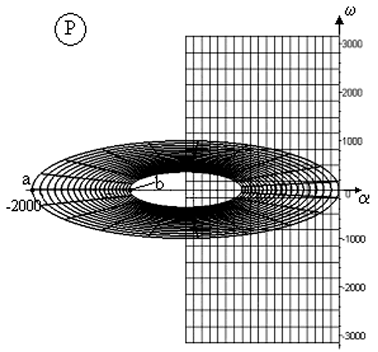
Рис. 2.3. Преобразование области устойчивости z-плоскости
на p-плоскость для метода прямой разности
Необходимо также учитывать, особенно на границах устойчивости, что полюса системы можно определить с некоторой погрешностью по затуханию Δα и по частоте Δω. Тогда условие (2.6) преобразуется к виду
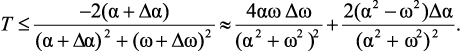(2.7)
В z-плоскости погрешности по затуханию и по частоте будут давать погрешности по действительной Δx = TΔα и по мнимой частям Δy = TΔω.
Метод обратной разности. Используя формулу перехода
p = (z – 1)/(zT), выразим z-переменную через p-переменную:
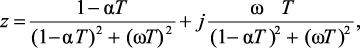(2.8)
где
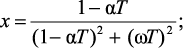
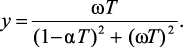(2.9)
С учетом обозначений (2.1), (2.2) получим:
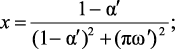
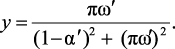(2.10)
Определим модуль и аргумент z:
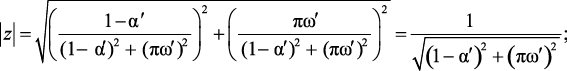(2.11а)
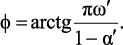(2.11б)
Отображение по формулам (2.11) области полюсов в p-плоскости на z-плоскость показано на рис. 2.2, б, согласно которому при всех параметрах численное решение устойчиво, причем с некоторым запасом. Рассматриваемое преобразование отображает левую полуплоскость р переменной в круг половинного радиуса с центром в точке Re(z) = 1/2.
Если один из полюсов системы расположен близко к точке (0; 0) в p-области, то необходимо учитывать погрешность при отображении этого полюса на z-плоскость, чтобы система не вышла из области устойчивости при применении данного метода. Точка (1; 0) является единственной точкой, находящейся на границе области устойчивости z-плоскости при данном преобразовании.
Метод Тустена. Используя формулу перехода p = 2(z – 1)/((z + 1)T), выразим z-переменную через p-переменную:
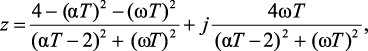(2.12)
где
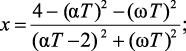
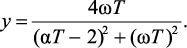(2.13)
Тогда с учетом новых переменных (2.1), (2.2) получим:
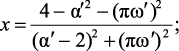
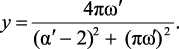(2.14)
Определим модуль и аргумент z:
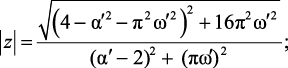(2.15а)
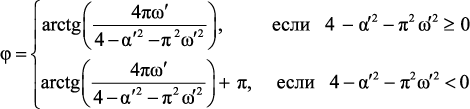(2.15б)
На рис. 2.2, в показано отображение p-области на z-плоскость с помощью формул (2.15), которое является частью области единичного круга и поэтому при всех параметрах численное решение устойчиво. При данном преобразовании границей устойчивости является отрезок 2-5 в p-плоскости (α′ = 0), который преобразуется в часть единичной окружности.
Дискретное интегральное преобразование без потерь. Данное преобразование также является алгебраическим преобразованием плоскости комплексной переменной p на z-плоскость при подстановке:
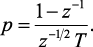(2.16)
Выразим z-переменную через p-переменную, зная, что p = α + jω:
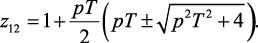(2.17)
Выполним преобразование выражения (2.17), используя показательную форму записи комплексных чисел и новые переменные, по формулам (2.1), (2.2). Получим
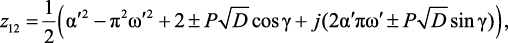(2.18)
где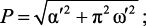 
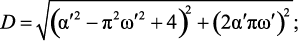
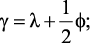
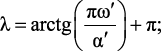
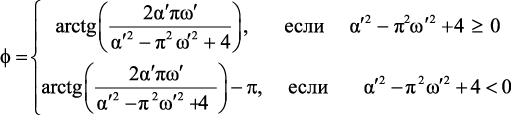
Определив модуль и аргумент z1, найдем отображение p-области в z-область (рис. 2.2, г). Анализ конформного отображения (рис. 2, г) показывает, что область устойчивости из p-плоскости преобразуется практически в круг единичного радиуса на z-плоскости, однако численная модель не имеет запаса по устойчивости при z → 1. Аналогичное исследование проведено для z2, но в этом случае полученное отображение значительно превышает область круга единичного радиуса на z-плоскости.
При выводе z-формы, эквивалентной операторно-дискретному методу, при равенстве нулю параметра затухания в передаточной функции колебательного звена второго порядка получено выражение этой z-формы. Поскольку в операторно-дискретном методе в качестве математических моделей используются схемы замещения и применяются две z-формы, а именно прямая и обратная разности, то исследовать устойчивость этого метода с помощью трансформации областей устойчивости с p-плоскости на z-плоскость невозможно.