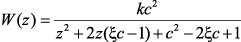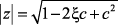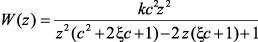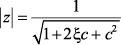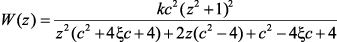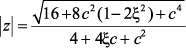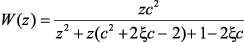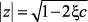Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
2.4. Устойчивость цифровых моделей типового звена
При выборе метода численного моделирования для конкретной задачи необходима информация о потенциальных возможностях каждого метода. Из проведенного ранее анализа областей устойчивости следует, что при использовании метода обратных разностей область устойчивости на p-плоскости трансформируется в некоторую область на z-плоскости с наибольшим запасом по устойчивости, а метод прямых разностей может дать неустойчивое численное решение при устойчивом решении аналоговой модели. Однако с помощью метода трансформации областей устойчивости не представляется возможным исследовать операторно-дискретный метод, поскольку в нем одновременно используется две z-формы (прямая и обратная разности), а в качестве исходной модели операторная схема замещения. Для метода прямой разности выявлена область недопустимых значений полюсов непрерывной передаточной функции, однако сравнительно сложно выявить условия выбора численных значений полюсов. Поэтому для определения численных значений границ проведено исследование моделирования типового звена, а именно колебательного звена второго порядка. Данное звено характеризуется двумя параметрами периодом T0 и параметром затухания ξ, которые однозначно связаны с переменными ω и α комплексной плоскости.
Такое исследование обладает большой общностью, поскольку дифференциальное уравнение второго порядка и классический метод его решения достаточно известны из курсов математики, механики и электротехники и используется для моделирования различных систем. Уравнения второго порядка часто используются для приближенного описания звеньев систем автоматического управления и электротехнических устройств. В том случае, если исследуемые линейные системы описываются дифференциальным уравнением более высокого порядка, то, как было доказано А.Ю. Ишлинским, переходный процесс приближенно можно описать уравнением второго порядка [49]. Обычно реальные динамические системы характеризуются парой доминирующих полюсов, а остальные находятся далеко слева, тогда влияние последних на передаточную функцию незначительно и поэтому в этом случае переходный процесс приближенно можно описать уравнением второго порядка. Кроме того, в цифровых системах управления колебательное звено второго порядка используется при каскадной реализации алгоритмического управления и является технической характеристикой сигнального процессора, то есть колебательное звено второго порядка можно принять в качестве элементарного процессора цифровой системы управления [4].
Передаточная функция колебательного звена второго порядка:
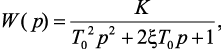 (2.24)
(2.24)
где K – передаточный коэффициент; T0 – постоянная времени; ξ – относительный коэффициент затухания (0 < ξ < 1 – для колебательного режима).
Из анализа результатов, полученных в работах [76, 81], следует, что погрешность цифрового моделирования зависит от значений периода дискретизации, параметра затухания динамического звена. При стремлении периода дискретизации к нулю, то есть при приближении численной модели к аналоговой модели, уменьшается погрешность моделирования, но при этом увеличивается объем обрабатываемой информации. Кроме того, в источнике [37] приведены результаты анализа, из которых следует, что с уменьшением периода дискретизации модули полюсов импульсной передаточной функции стремятся к единице, то есть к области неустойчивости. Поэтому для разработки методик моделирования динамических звеньев необходимо провести исследования устойчивости численного решения. Полученные результаты позволят обоснованно выбирать методы моделирования и параметры численных моделей.
Проведем исследования чувствительности к устойчивости решения различных методов [77]. Для этого с помощью различных методов осуществим переход к импульсной передаточной функции:
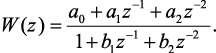 (2.25)
(2.25)
Для выражений импульсных передаточных функций, полученных с помощью разных методов аппроксимации, определим модули полюсов и проведем их исследование в зависимости от параметров модели. Для устойчивости численного моделирования необходимо, чтобы значения модулей полюсов импульсной передаточной функции были меньше единицы.
2.4.1. Анализ устойчивости цифровых моделей типового звена, полученных с помощью z-форм
Прямая разность. Исследуем изменение  в зависимости от относительного коэффициента затухания ξ и относительной величины периода дискретизации c, а результаты исследования представим в виде графических зависимостей. Аналогичные исследования будут проведены для других методов. Используя подстановку
в зависимости от относительного коэффициента затухания ξ и относительной величины периода дискретизации c, а результаты исследования представим в виде графических зависимостей. Аналогичные исследования будут проведены для других методов. Используя подстановку
p = (z – 1)/T (2.26)
в (2.24), и, введя переменную c = T/T0, где Т – период дискретизации, получим выражение для импульсной передаточной функции:
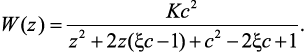 (2.27)
(2.27)
Определим z-полюса функции W(z) и их модуль:
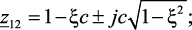 (2.28)
(2.28)
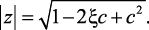 (2.29)
(2.29)
Обратная разность. Проведем исследование с использованием метода обратных разностей. С помощью подстановки p = (z – 1)/zT в (2.24), получим дискретную передаточную функцию:
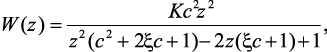 (2.30)
(2.30)
тогда z-полюса функции W(z) и их модуль имеют вид:
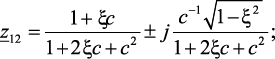 (2.31)
(2.31)
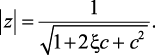 (2.32)
(2.32)
Метод трапеций. Аналогично предыдущим методам, путем замены p = 2(z – 1)/T(z + 1) в формуле (2.24) получено выражение функции W(z):
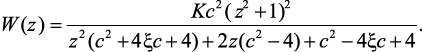 (2.33)
(2.33)
Выражения для z-полюсов функции W(z) и их модуля имеют вид:
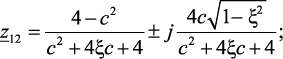 (2.34)
(2.34)
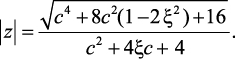 (2.35)
(2.35)
2.4.2. Анализ устойчивости цифровых моделей, полученных с помощью операторно-дискретного метода
Операторно-дискретный метод в качестве исходной информации использует электрические схемы замещения, поэтому дальнейшее исследование проведем на примере четырехполюсника, для которого с помощью операторно-дискретного метода получена дискретная схема замещения (рис. 2.10) [80].
Схеме замещения, изображенной на рис. 2.10, соответствует дискретная передаточная функция:
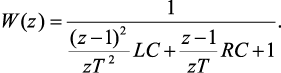 (2.36)
(2.36)
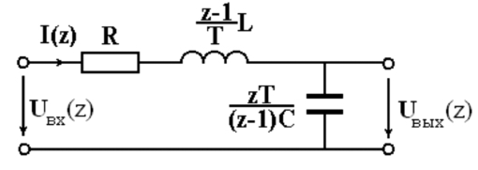
Рис. 2.10. Дискретная схема замещения четырехполюсника
Проанализируем устойчивость операторно-дискретного метода моделирования, исследуя зависимость модуля полюсов передаточной функции четырехполюсника от периода дискретизации. Выполнив математические преобразования и введя замену c = T/T0, 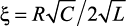 , получим:
, получим:
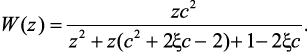 (2.37)
(2.37)
По выражению передаточной функции (2.37) определим z-полюса и их модуль:
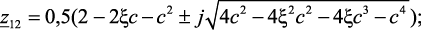 (2.38)
(2.38)
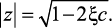 (2.39)
(2.39)
Из выражения (2.36) следует, что формула замены оператора p при коэффициенте, характеризующем процесс затухания колебаний, соответствует обратной разности, а формула перехода от оператора p при коэффициенте, характеризующем период колебаний, имеет следующий вид:
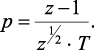 (2.40)
(2.40)
Выражение (2.40) является формой перехода плоскости комплексной переменной p на z-плоскость при дискретном интегральном преобразовании без потерь. Поскольку при моделировании используется ряд Лорана с целыми степенями, то выражение 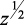 разложим в ряд Тейлора в окрестности точки z0 = 1, и, ограничившись первыми двумя членами ряда, получим формулу для приближенной замены:
разложим в ряд Тейлора в окрестности точки z0 = 1, и, ограничившись первыми двумя членами ряда, получим формулу для приближенной замены:
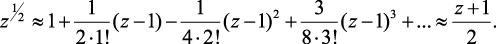 (2.41)
(2.41)
Тогда согласно формуле (2.40):
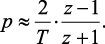 (2.42)
(2.42)
Формула (2.42) полностью совпадает с формулой перехода по способу трапеций. Выражение (2.40) также представляет собой произведение формулы перехода для прямой разности и оператора сдвига на половину периода z‒1/2 [82].
2.4.3 Сравнительный анализ устойчивости цифровых моделей
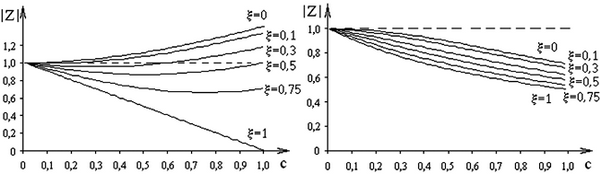
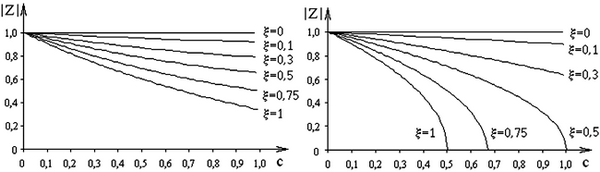
Графические зависимости модулей полюсов передаточных функций  от относительного периода дискретизации с, при 0 < c < 1 и различных ξ представлены на рис. 2.11. Аналитические выражения модулей z для всех методов приведены в табл. 2.1.
от относительного периода дискретизации с, при 0 < c < 1 и различных ξ представлены на рис. 2.11. Аналитические выражения модулей z для всех методов приведены в табл. 2.1.
а б
в г
Рис. 2.11. Зависимости 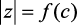 при различных ξ для методов:
при различных ξ для методов:
а – прямой разности; б – обратной разности; в – трапеций;
г – операторно-дискретного метода
Анализ зависимостей  от с относительно границы устойчивости
от с относительно границы устойчивости 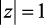 , показывает, что при ξ → 0 запасом по устойчивости обладает метод обратной разности (рис. 2.11, б), так как значения функции
, показывает, что при ξ → 0 запасом по устойчивости обладает метод обратной разности (рис. 2.11, б), так как значения функции 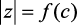 достигают критического значения
достигают критического значения 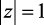 только при ξ → 0 и c → 0, при этом, коэффициент затухания ξ оказывает наименьшее влияние на устойчивость численного решения. В методе прямой разности часть графиков пересекает границу устойчивости, что накладывает ограничения на применение этого метода (рис. 2.11, а). Например, при ξ = 0,1 период дискретизации с, при котором численное решение устойчиво, принадлежит интервалу (0; 0,2]; при ξ = 0,2 – (0; 0.4]; ξ = 0,3 – (0; 0,6].
только при ξ → 0 и c → 0, при этом, коэффициент затухания ξ оказывает наименьшее влияние на устойчивость численного решения. В методе прямой разности часть графиков пересекает границу устойчивости, что накладывает ограничения на применение этого метода (рис. 2.11, а). Например, при ξ = 0,1 период дискретизации с, при котором численное решение устойчиво, принадлежит интервалу (0; 0,2]; при ξ = 0,2 – (0; 0.4]; ξ = 0,3 – (0; 0,6].
Таблица 2.1
Аналитические выражения дискретных передаточных функций и модулей полюсов для различных методов аппроксимации
|
Вид |
Дискретная передаточная функция |
Модуль |
|
Прямая разность |
|
|
|
Обратная разность |
|
|
|
Метод трапеций |
|
|
|
Операторно-дискретный метод |
|
|
Графические зависимости для метода трапеций и операторно-дискретного метода (рис. 2.11, в, г) не выходят из области устойчивости, но при ξ → 0 модуль z стремится к единице. Поэтому данные методы могут дать неустойчивое численное решение, что обусловлено погрешностями округления и накопления, возникающими при использовании рекуррентной формулы для определения оригинала.
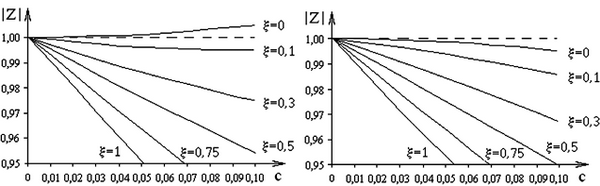
С точки зрения исследования устойчивости наиболее интересны области значений модулей z при значениях относительного периода дискретизации 0 < с ≤ 0,1, применяемых на практике, поэтому на рис. 2.12 представлены зависимости 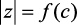 в указанном диапазоне с.
в указанном диапазоне с.
Выводы. При использовании z-форм получены модели конформных преобразований между p и z-областями для различных форм аппроксимации, позволяющие определять параметры численных моделей и степень искажения частотных характеристик с помощью введенного коэффициента линейности. При использовании метода прямой разности при дискретизации устойчивая система может перейти в область неустойчивости. В остальных случаях преобразование из p-области в z-область происходит с некоторым запасом по устойчивости.
а б
в г
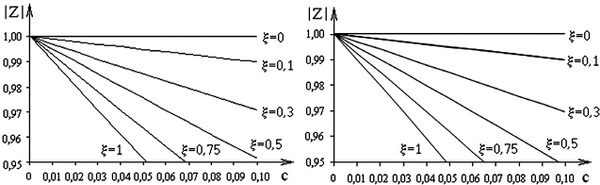
Рис. 2.12. Зависимости 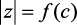 (0 < c< 0,1) при различных ξ для методов:
(0 < c< 0,1) при различных ξ для методов:
а – прямой разности; б – обратной разности; в – трапеций;
г – операторно-дискретного метода
На основе проведенного исследования влияния основных параметров численной модели, а именно, соотношения с = Т/Т0 и параметра затухания ξ на устойчивость дискретной модели колебательного звена второго порядка, можно сделать вывод, что при c → 0 модуль z тестируемой функции стремится к границе устойчивости 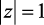 при использовании рассмотренных z-форм и операторно-дискретного метода.
при использовании рассмотренных z-форм и операторно-дискретного метода.
Из анализа графических зависимостей 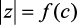 следует, что при моделировании колебательного звена метод прямой разности при значении ξ ≤ 0,4 не может быть использован, запас по устойчивости имеет метод обратной разности, что является ценным фактом, поскольку этот метод используется в экстраполяторах цифровых систем управления, работающих в реальном масштабе времени.
следует, что при моделировании колебательного звена метод прямой разности при значении ξ ≤ 0,4 не может быть использован, запас по устойчивости имеет метод обратной разности, что является ценным фактом, поскольку этот метод используется в экстраполяторах цифровых систем управления, работающих в реальном масштабе времени.