Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
3.1. Анализ причин формирования погрешностей цифрового моделирования
При преобразовании аналогового сигнала в цифровой выполняются две основные операции: временная дискретизация и квантование по уровню. При выполнении этих операций возникают погрешности и поэтому для разработки методики использования методов цифрового моделирования необходимо выявление источников формирование погрешностей и их анализ. Как указывалось выше, структура рекурсивного алгоритма полностью совпадает со структурой цифрового фильтра, реализующего этот алгоритм [87]. Следовательно, анализ погрешностей рекурсивного алгоритма можно проводить теоретически и экспериментально на цифровом фильтре.
Погрешности дискретизации. Теоретически процесс дискретизации аналогового сигнала приведен при выводе теоремы Котельникова, согласно которой для передачи информации без искажений частота дискретизации должна быть в два раза больше высшей частотной составляющей аналогового сигнала. Однако эта теорема применима для идеализированного случая, а именно частотный спектр аналогового сигнала должен быть ограничен, а временной соответственно неограничен, а при восстановлении сигнала должен быть использован идеальный фильтр с прямоугольной частотной характеристикой и использован ряд Котельникова. Таким образом, теорема Котельникова имеет фундаментальное значение. На практике в цифровых системах управления при восстановлении сигнала используется устройство выборки и хранения, представляющее собой экстраполятор нулевого порядка. Поэтому выбор частоты дискретизации в цифровых системах управления по теореме Котельникова может не обеспечить требуемой точности или даже нормальной работы. Из анализа проведенных исследований [16] следует, что при восстановлении гармонической функции с помощью экстраполятора нулевого порядка с погрешностью не более 1 % частота дискретизации должна быть больше основной частоты в 22 раза. Выбор частоты дискретизации должен выполняться из условия компромисса между точностью преобразования и объемом выполняемых операций в единицу времени, то есть быстродействием цифровой системы. Погрешность и быстродействие цифровой системы зависит от алгоритма обработки информации погрешностей квантования по уровню. Поэтому для разработки методик обоснованного выбора частоты дискретизации необходимы экспериментальные исследования погрешностей типовых динамических звеньев.
Погрешности квантования в цифровых системах. При анализе точности цифровых систем обычно выделяются три источника погрешностей: квантование входного сигнала, квантование коэффициентов фильтра (передач и передач с задержкой) и округление результатов арифметических операций. Из этих трех источников погрешности округления является наиболее существенной. Погрешность квантования коэффициентов цифрового фильтра вызывает искажение его частотной характеристики в сравнении с частотной характеристикой аналоговой модели, а также может привести к неустойчивости фильтра [5, 19, 20].
Погрешность квантования входного сигнала. Квантование входного сигнала осуществляется аналого-цифровым преобразователем. При этом входной сигнал периодически дискретизируется и каждая выборка кодируется в цифровое слово длиной В бит. Погрешность квантования входного сигнала ограничивается половиной шага квантования. Для большинства входных сигналов последовательность {e(n)} может рассматриваться как белый шум, статистически не зависящий от исходной последовательности, и поэтому ее называют шумом квантования. Белый шум – это абсолютно случайный процесс, обладающий равномерным спектром в очень широком диапазоне частот [4]. Понятие белого шума – это удобная абстракция, поскольку средний квадрат такого процесса равен бесконечности вследствие того, что площадь, ограниченная функцией спектральной плотности, бесконечна. Понятие белого шума оказывается полезным при анализе линейных систем, особенно в тех случаях, когда ширина спектральной плотности сигнала на входе системы значительно шире полосы пропускания этой системы или время корреляции шума много меньше всех существующих постоянных времени системы, на которую воздействует шум. Таким образом, предположение, что входной сигнал является белым шумом, значительно упрощает решение задачи.
В линейной системе с передаточной функцией W(z) и стационарным входным сигналом {un} выходной сигнал {υn} тоже будет стационарным [4]. Обычно предполагается, что входная последовательность является белым шумом, имеет нулевое среднее и дисперсию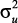 
, то есть
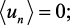
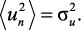(3.1)
Стационарный случайный процесс принято описывать двумя характеристиками – спектральной плотностью G(z) и автокорреляционной функцией В(τ). Для белого шума эти характеристики соответственно равны 1(z) и δ(τ). Спектральные плотности входной и выходной последовательностей для стационарного случайного процесса связаны соотношением:
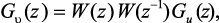(3.2)
где W(z–1) величина комплексно-сопряженная W(z), z = ejλ и λ = 2πf/F, f, F – частоты аналогового сигнала и дискретизации.
Автокорреляционная функция вычисляется по формуле Винера-Хинчина
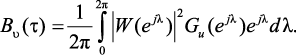(3.3)
При τ = 0 имеем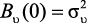 
, и тогда значение спектральной плотности для белого шума 1(ejλ) определяется выражением
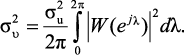(3.4)
В общем случае, когда {un} не является белым шумом, но сохраняет стационарность и имеет нулевое среднее значение и спектральную плотность мощности Φuu(z), его дисперсия
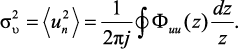(3.5)
Выходной сигнал в этом случае также является стационарным случайным процессом с нулевым средним, спектральной плотностью мощности и дисперсией соответственно
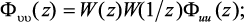
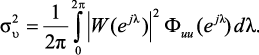(3.6)
В соответствии с этим входной сигнал представляется в виде двух аддитивных составляющих: исходной {x(n)} и шум квантования {e(n)}. В соответствии с принципом суперпозиции для линейного цифрового фильтра выходной сигнал также состоит из двух аддитивных составляющих: идеального выходного сигнала {y(n)} и сигнала погрешности, вызванной входным шумом {e(n)}.
Сигнал погрешности определяется выражением:
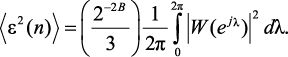(3.7)
Погрешность квантования коэффициентов. При практической реализации фильтра с передаточной функцией
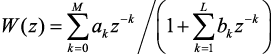(3.8)
коэффициенты всегда квантуются. Если αk и βk – погрешности квантования коэффициентов, удовлетворяющие условиям: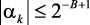 
и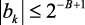 
,
то реальные коэффициенты имеют вид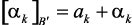 
, 
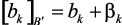, где B’ число бит для представления коэффициентов. В результате передаточная функция принимает следующий вид
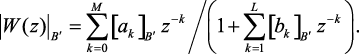(3.9)
Смещение полюсов и нулей передаточной функции вследствие квантования коэффициентов можно определить по формуле:
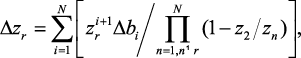(3.10)
где Δbi – изменение коэффициента bi, z1 z2 ... zr – положение полюсов идеального фильтра. Доказано, что чувствительность смещения полюсов к коэффициентам увеличивается с ростом порядка фильтра при прямой форме реализации. Таким образом, реализация фильтра выше второго порядка в прямой форме нежелательна. В этом случае предпочтительнее параллельная или каскадная форма. Если полюсы близко расположены к единичной окружности в z-плоскости, то в результате их смещения фильтр может стать неустойчивым.
Погрешность округления. Как указывалось выше, основной погрешностью в цифровых в рекурсивных фильтрах является погрешность округления [4], которая накапливается за счет перехода из предыдущих состояний в последующие. Точное значение отсчета сигнала в двоичной форме определяется выражением
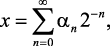(3.11)
где αn = 0 или 1.
При округлении длины x некоторым количеством разрядов N вместо точного значения получается его округленное (машинное) представление. Существуют два способа выполнения этой операции: усечение или округление. При усечении сохраняются старшие N бит, а все младшие разряды усекаются, а при округлении выполняется операция согласно формуле
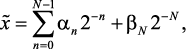(3.12)
причем коэффициент βN равен αn или αn + 1 в зависимости от того, нуль или единица содержится в (N + 1)-м разряде.
Округление является более точным, чем усечение, но аппаратно реализуется сложнее и требует больших затрат времени. По этой причине чаще применяется первый способ.