Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
4.4. Моделирование нелинейных электротехнических устройств
В качестве нелинейного звена рассмотрим синхронный генератор, математическая модель которого представлена дифференциальным уравнение движения ротора генератора:
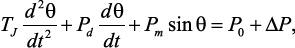(4.15)
где ТJ и Pd – коэффициенты, определяющие частоту и затухание колебаний; θ – угол сдвига фаз ЭДС генератора относительно напряжения на его выходе; Рm –максимальное значение активной мощности, выдаваемой генератором; Р0 – мощность турбины. Решение уравнения (4.15) определяет не только физику явления, но используется для определения времени срабатывания релейной защиты, скорости действия регулирующих устройств, скорости подъема возбуждения [38].
Даже для простейшей энергетической системы, возникает проблема анализа переходного процесса, так как генератор имеет нелинейную характеристику, которая обусловлена функциональной зависимостью между параметрами режима P и θ. На рис. 4.14 показана характеристика мощности синхронного генератора. Формальным признаком статической устойчивости электрической системы является знак приращения мощности к приращению угла. Если dP/dθ > 0, то система устойчива, если dP/dθ < 0, то система неустойчива.
В настоящее время при анализе переходных процессов в энергетической системе решаются две различные по постановке задачи: исследование переходных процессов в линеаризованной системе и с учетом нелинейностей. При малых возмущающих воздействиях используются линейные методы анализа, то есть используется разложение нелинейной зависимости в уравнении (4.15) в ряд Тейлора при отклонении от
состояния равновесия, и учитываются только линейные члены ряда, а при больших возмущениях применяются методы нелинейной теории [38, 62, 63].
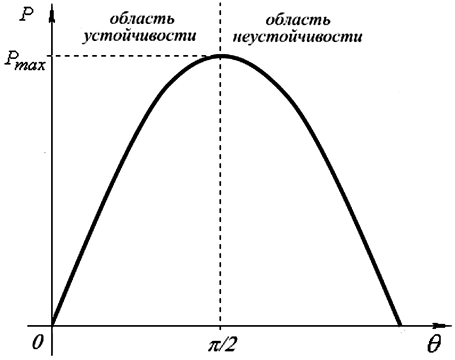
Рис. 4.14. Характеристика мощности генератора
Однако такое разделение задач анализа статической и динамической устойчивости условно, так как генератор имеет единую характеристику мощности. Если использовать единую теорию анализа устойчивости объектов энергосистем, то нет необходимости в разделении задач устойчивости на статическую и динамическую. Однако для создания такой теории необходим математический аппарат анализа как линейных, так и нелинейных систем.
Незначительное возмущение в цепи статора генератора вызывает движение ротора в сторону увеличения или уменьшения угла θ между ЭДС и напряжением на выходе генератора U. Уравнение движения ротора генератора описывается нелинейным дифференциальным уравнением:
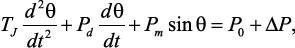(4.16)
где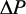 
– возмущающее воздействие.
При малых возмущающих воздействиях при решении данного уравнения используется разложение нелинейной функции в ряд Тейлора, причем все нелинейные члены ряда не учитываются (линеаризованный участок 0-1 на рис. 4.15).
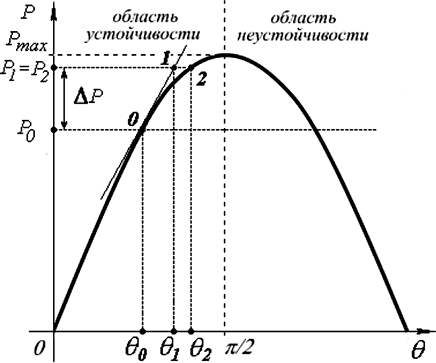
Рис. 4.15. Характеристика мощности синхронного генератора
Воспользуемся методом z-форм для численного решения уравне-
ния (4.16). При выборе способа аппроксимации и параметров численной модели воспользуемся результатами анализа методов z-форм, проведенного ранее. Рассмотрим методику моделирования переходной характеристики генератора при следующих значениях параметров: TJ = 0,1 с; Pd = 1,5 c; Рm = 100 Вт; ∆Р = 1 Вт; θ = π/4 рад.
Методика моделирования
Линеаризация дифференциального уравнения. С помощью формальной замены Рmsinθ ≈ μθ в (4.16) получим линейное дифференциальное уравнение с переменными коэффициентами:
(4.17)
Алгебраизация дифференциального уравнения. Используя прямое преобразование Лапласа к уравнению (4.17), получим алгебраическое уравнение:
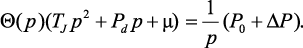(4.18)
где Θ(p) – операторное изображение функции θ(t); 1/p – операторное изображение функции Хевисайда.
Получим выражение передаточной функции. В качестве воздействия рассмотрим – 1/p, а в качестве реакции – Θ(p):
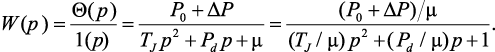(4.19)
Выберем форму аппроксимации. Для колебательного звена по рекомендациям, представленным в главе 2, выбираем форму аппроксимации – метод обратной разности. Это связано с тем, что довольно часто в литературе в качестве модели используется колебательное звено без затухания, и только метод обратных разностей в области с малым значением ξ обеспечивает запас устойчивости в отличие от других методов.
Выберем период дискретизации Т. Период дискретизации для заданных значений выбирается для первого такта вычислений, поскольку крутизна характеристики мощности в начальной точке имеет большее значение в сравнении с каждой последующей при перемещении к области неустойчивости. Методика выбора значения периода дискретизации аналогична методике выбора для линейного звена. Для этого определим параметры колебательного звена: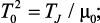 
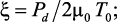
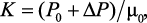где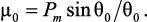 
Для данной задачи при предельной погрешности δпр = 0,001, период дискретизации для метода обратной разности – T = cT0 = 5·10–4 c.
Дискретизация передаточной функции. С помощью метода z-форм перейдем от непрерывной передаточной функции (4.19) к дискретной, используя подстановку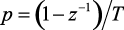 
согласно обратной разности:
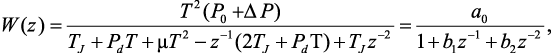(4.20)
где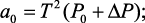 
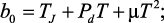
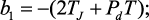b2 = Tj.
Алгоритм вычислений значений искомой функции в тактовые моменты времени:
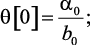
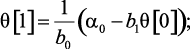
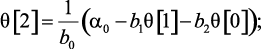
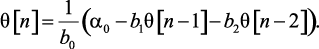(4.21)
Для учета нелинейности, а именно Pmsin θ, в каждом такте вычисления по найденной функции θ[n] корректируется эквивалентный коэффициент μ, используя соотношение:
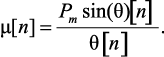(4.22)
На рис. 4.16 представлены графики численного решения нелинейного уравнения (график 1) и линеаризованного (график 2). С помощью предложенного метода линеаризация осуществляется в каждом такте вычислений, при этом рабочая точка на характеристике мощности генератора перемещается из точки 0 в точку 2 (рис. 4.15).
Для проверки точности численного решения с учетом нелинейности использовалось вычисление установившегося значения переходной функции. Для вычисления погрешности сравнивались два значения θ2, полученные с помощью вычисления по тригонометрической функции (образцовое значение) и с помощью рекурсивного алгоритма. Для заданных значений θ0, Р0 и ΔР, определим координаты точки 2: Р2 = Р0 + ΔР, так как Р2 = Pmsinθ2, получим θ2 = arcsin(P/Pm). При заданных параметрах относительная погрешность численного решения составляет 5,651∙10–3 %.
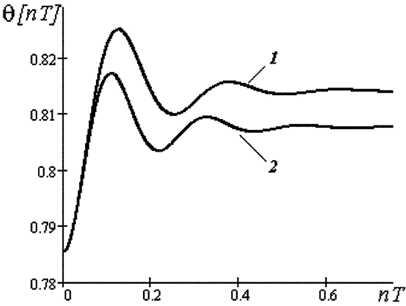
Рис. 4.16. Переходные характеристики нелинейной (1)
и линеаризованной (2) систем
Оценка эффективности использования численного моделирования. Для оценки повышения точности численной модели в сравнении с использованием линеаризации определим значения погрешности, которая исключается при численном моделировании. При использовании
линеаризованной модели на всем участке рабочая точка перемещается по характеристике из точки 0 в точку 1, а при использовании более точной модели с линеаризации в каждом такте вычислений точка перемещается из 0 в 2 (рис. 4.15). Из сравнения результатов получены значения абсолютной погрешности моделирования с помощью упрощенной модели (рис. 4.17).
С помощью метода интегральных оценок получено, что в рабочей точке 0,707Pm на характеристике мощности генератора (рис. 4.15) в диапазоне (0,707...0,717) Pm точность моделирования нелинейной модели относительно линейной повышена на 21,5 %. Кроме того, в процессе вычисления переходной функции в каждом такте определяются параметры колебательного звена, и программа позволяет осуществлять контроль по условиям устойчивости и точности. Если параметры выходят за пределы допустимых значений, то может корректироваться период дискретизации.
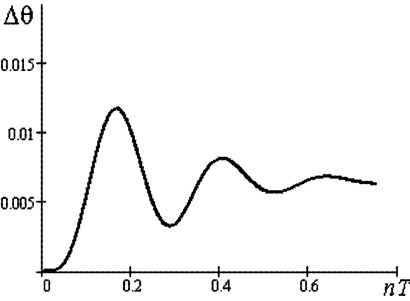
Рис. 4.17. График абсолютной погрешности линеаризованной системы
Таким образом, с помощью линейной модели, параметры которой корректируются в процессе вычислений, решается нелинейная задача. Для проверки этого алгоритма была решена тестовая задача, описывающая переходный процесс в колебательном звене второго порядка, причем значения μ каждый раз менялись, и выполнялась проверка по соблюдению требований точности и устойчивости. В результате проведенных исследований подтвердилось положение о том, что выбранные параметры численной модели в рабочей точке характеристики обеспечивали требования во всем диапазоне моделирования.
Вывод. В результате моделирования нелинейных процессов с помощью z-форм получены рекурсивный алгоритм и программа, позволяющие осуществлять моделирование электромеханических переходных процессов без линеаризации с более высокой точностью во всей области устойчивой работы генератора. Таким образом, на примере простой задачи показана эффективность расчета переходных процессов в энергетической системе с помощью метода z-форм с учетом нелинейности. Кроме того, этот алгоритм может использоваться для решения задач статической и динамической устойчивости системы без их условного разделения.