Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
4.6. Моделирование систем с коммутирующими элементами
В настоящее время в электроэнергетике одной из основных теоретических проблем является анализ динамических процессов в системах с коммутирующими устройствами. Такие процессы возникают, например, при переключении секций трансформаторов, при коммутации сетей электроснабжения, а также процессов, протекающих в импульсных устройствах (блоках питания, электроприводах, технологических установках).
В результате работы коммутирующих устройств в сети возникают высшие гармонические составляющие, которые отрицательно влияют на окружающую среду, работу радиоэлектронной аппаратуры, качество электрической энергии, а также являются источниками дополнительных энергетических потерь.
В связи с перспективой внедрения в энергетике интеллектуальных электрических сетей относительная доля систем коммутации будет непрерывно увеличиваться. Поэтому при их внедрении необходим предварительный анализ физических процессов, протекающих в сети. Такой анализ позволяет обоснованно определять конструкцию систем коммутации, их параметры и устройства для компенсации отрицательных явлений (фильтров).
Проблема анализа заключается в том, что довольно сложно математически описать переходные процессы в импульсных системах. Обычно такие системы анализируются с помощью составления решения дифференциальных уравнений для каждого импульса, что является довольно трудоемкой операцией, поскольку необходимо определять реакцию системы на каждом этапе коммутации, причем начальные условия на каждом этапе изменяются. Для решения этой проблемы предлагается использовать операторно-дискретный метод, позволяющий сравнительно просто получать численные уравнения динамических процессов.
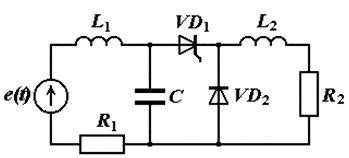
Рассмотрим методику моделирования систем с коммутирующими элементами с помощью операторно-дискретного метода на примере двигателя постоянного тока с тиристорным управлением. На рис. 4.28 представлены электрические схемы замещения устройства при замкнутом и разомкнутом ключе.
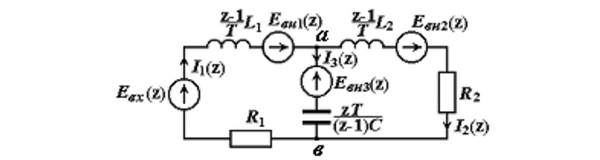
Составим схемы замещения согласно операторно-дискретному методу (рис. 4.29). С помощью метода узловых потенциалов, законов Ома и Кирхгофа получены z-изображения токов и напряжений. Выражение для z-изображения напряжения Uab(z) (рис. 4.29, а) имеет следующий вид:
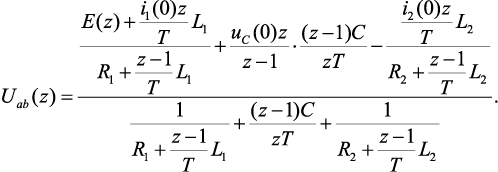(4.58)
а
б в
Рис. 4.28. Электрическая схема цепи с коммутирующим элементом:
а – общая схема замещения; б – схема замещения до размыкания ключа;
в, г – схемы замещения после размыкании ключа
а
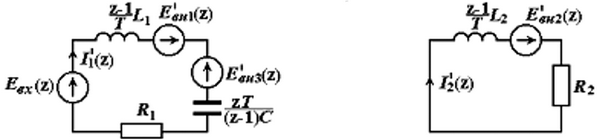
б в
Рис. 4.29. Операторно-дискретная схема цепи с коммутирующим элементом:
а – схема замещения до размыкания ключа;
б, в – схемы замещения после размыкании ключа
Выполнив математические преобразования, получим
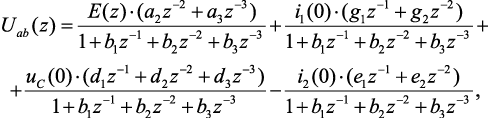(4.59)
где коэффициенты полиномов числителей:
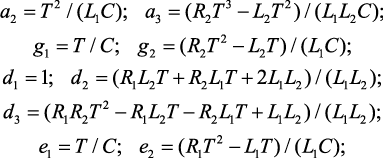
коэффициенты полиномов знаменателей:
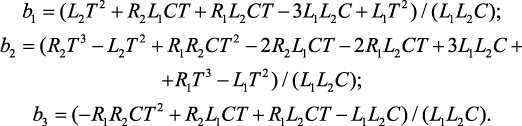
По закону Ома в дискретной форме получены z-изображения токов ветвей до размыкания ключа (рис. 4.29, а):
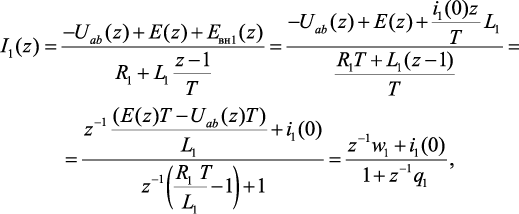(4.60)
где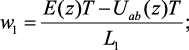 
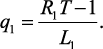
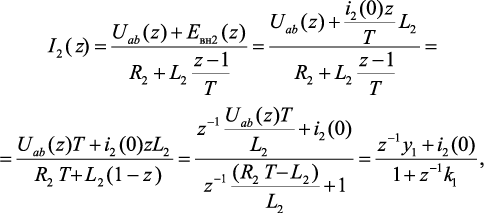(4.61)
где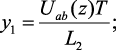 
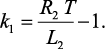
Аналогично были получены z-изображения токов ветвей после размыкания ключа (рис. 4.29, б, в):
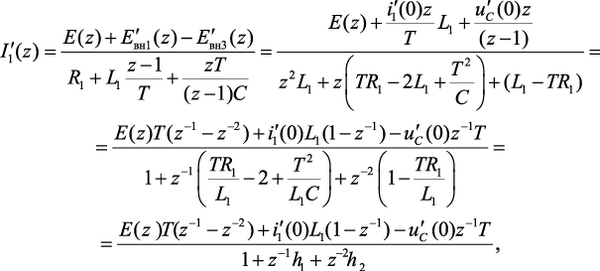(4.62)
где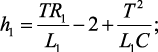 
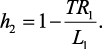
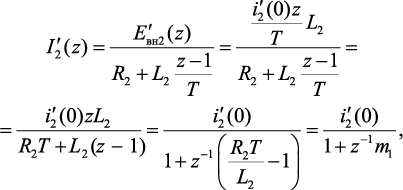(4.63)
где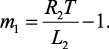 
Напряжение на конденсаторе после размыкания ключа (рис. 4.29, б):
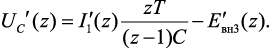(4.64)
Основными переменными во время до размыкания ключа являются значения [x], а после размыкания – [x′]:
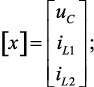
(4.65)
Для расчета значений функций оригиналов по полученным z-изображениям с помощью рекурсивных выражений (1.103) и (1.104), разработана компьютерная программа, структурная схема алгоритма которой представлена на рис. 4.30.
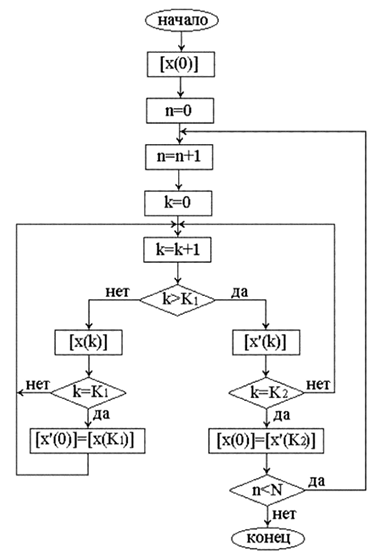
Рис. 4.30. Блок-схема алгоритма расчета значений функций оригиналов
Данная программа позволяет моделировать динамические процессы непрерывно в схеме с коммутирующим элементом. В этом алгоритме начальные значения каждого такта определяются по значениям в конце предыдущего такта.
В данном алгоритме использованы следующие обозначения:
[x(0)] – значения основных переменных состояния iL1, iL2, uC в начальный момент времени;
n – текущее дискретное значение основных переменных состояния;
k – промежуточная переменная – количество точек моделирования за один период K2 переменного несинусоидального сигнала (K2 = kT);
[x(k)] – значения основных переменных состояния iL1, iL2, uC в текущий момент времени;
K1 – время закрывания ключа (K1 < K2);
[x′ (0)] = [x′ (K1)] – значения основных переменных состояния iL1, iL2, uC в момент времени t = K1;
[x′ (k)] – значения основных переменных состояния iL1, iL2, uC в текущий момент времени;
[x(0)] = [x′ (K2)] – значения основных переменных состояния iL1, iL2, uC в момент времени t = K2; N – максимальное количество точек расчета.
Начиная с момента времени t = K2, цикл расчета по переменной k повторяется. На рис. 4.31 представлена реализация предложенного алгоритма расчета, а именно временная диаграмма изменения напряжения на конденсаторе. На диаграмме заштрихованные участки соответствуют интервалам времени, когда ключ закрыт, не заштрихованные интервалы – ключ открыт.
Рис. 4.31. Временная диаграмма изменения напряжения на конденсаторе
Вывод. Предложенный алгоритм операторно-дискретного метода позволяет сравнительно просто решать сложную задачу анализа переходных процессов в электрических цепях с коммутирующими элементами при различных возмущающих воздействиях, что обусловлено следующими особенностями метода: разностные уравнения довольно просто могут быть получены непосредственно из электрических схем без промежуточных операций составления непрерывных уравнений состояния и их дискретизации; возможность управления точностью расчета в процессе вычисления за счет изменения периода дискретизации.