Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Фрактальный анализ и синергетика катализа в наносистемах

Нафадзокова Л. Х., Козлов Г. В.,

1.1. Структурная модель странной (аномальной) диффузии в полимерах

Как известно [1-3], величина коэффициента диффузии D для одного и того же полимера может сильно варьироваться как функция размеров молекулы газа-диффузанта и температуры испытаний, а для разных полимеров как функция температуры стеклования (плавления). Это вариация может составлять несколько порядков величины. Поэтому для описания диффузионных процессов часто используют степенные функции [4-7]. Такая сильная вариация D предполагает деление процессов диффузии на медленные и быстрые [8]. В основу этого деления положена зависимость смещения молекулы газа S от времени t[9]:

S~t^b, (1.1)

где для классического случая b = 1/2, для медленной диффузии b <1/2 и для быстрой - b >1/2.

В рамках теории дробного дифференцирования было показано, что ее основной параметр - дробный показатель a связан и с b, и с характеристикой структуры - фрактальной (хаусдорфовой) размерностью d_f разными функциональными формами в зависимости от типа диффузии. Иначе говоря, структуры с одинаковыми d_f могут иметь очень различающиеся коэффициенты диффузии D. Поэтому авторы [10] исследовали возможность и условия реализации указанных типов диффузии в полимерах и предложили структурную модель, объясняющую изменение типа диффузии. Это было сделано на примере диффузии метана (СН₄) в 11 полимерах [2.11-13].

В работе [1] использована следующая зависимость D от молекулярной массы М газа-диффузанта:

D = КМ^-в_м, (1.2)

где К и в_м - константы.

Авторы [4] обнаружили систематическое увеличение показателя в_м с ростом температуры стеклования Т_с полимеров и объяснили наблюдаемую закономерность увеличением кинетической жесткости цепи по мере повышения Т_с. Однако, поскольку константы К и в_м являются эмпирическими, то это затрудняет прогнозирование величины D с помощью уравнения (1.2).

Величину коэффициента диффузии D в рамках фрактальной модели процессов газопереноса можно определить согласно уравнению [14-16]:

, (1.3)

где - универсальная константа, равная 3,8×10^-17см²/с, f_act-относительный свободный объём, d_n -диаметр микро полостей этого объёма, D_n-размерность структуры, контролирующая процессы газопереноса, d_s-спектральная размерность структуры, принятая для использованных в работе [10] 11 полимеров равной 1,0 [17].

В качестве размерности D_n в зависимости от величины (d_n/d_m) принимается либо фрактальная (хаусдорфова) размерность структуры d_f (приd_n/d_m>1,70) либо размерность областей локализации избыточной энергии (при d_n/d_m≤1,70) [18,19]. Величины d_f и связаны между собой соотношением [20]:

. (1.4)

Нетрудно видеть, что уравнения (1.2) и (1.3) дают одинаковую функциональную форму зависимости D от размера молекул газа-диффузанта: величина D быстро снижается в силу степенной зависимости по мере роста М или d_m. Однако, уравнение (1.3) не содержит эмпирических (подгоночных) параметров, что позволяет использовать его для прогнозирования D. Величина показателя 2 (D_n - d _s) / d _s может быть определена по закону линейных графиков D (1/ d_n) в двойных логарифмических координатах. На рис. 1.1 приведена зависимость определенной таким способом размерности D_n от разности температур стеклования Т_с (или плавления Т_пл для аморфно-кристаллических полимеров) и испытаний Т для 11 полимеров. Как можно видеть, до [Тс (Т_пл) - Т] < 120К наблюдается слабый рост D_n, а выше указанной разности температур величина D_n растет значительно быстрее. Из уравнения (1.3) следует, что размерность D_n вносит основной вклад в изменение коэффициента диффузии полимеров при d_{m =} const в силу степенного характера этого уравнения и поскольку изменения характеристик флуктуационного свободного объема f_s и d_n невелико и антибатно [21]. Поэтому D_n можно принять в качестве некоторой основной обобщенной характеристики диффузии в полимерах [10].

Резкое изменение зависимости D_n от [Т_с(Т_пл)-Т] при значении последнего параметра ~ 120К предполагает, что эта приведенная температура является границей между медленной и быстрой диффузией. Взаимосвязь d_f и a для трехмерного евклидова пространства можно получить по аналогии с работой [9] следующим образом. Полагаем, что показатель Херста Н связан с d_f уравнением [10]:

Рис.1.1. Зависимость размерности D_n, контролирующей процессы газопереноса, от разности температур стеклования Т_с (плавления Т_пл) и испытаний Т.1 - экспериментальные данные;2 - расчет по уравнению (1.8) [10].

 d_f = 3 - Н (1.5)

Авторы [9] показали, что в уравнении (1.1) показатель b равен (1 - a)/2 для медленной диффузии и 1/(1 + a) - для быстрой. Приравнивая Н указанным выражениям для a согласно методике [9], получим взаимосвязь a и d_f:

(1.6)

для медленной диффузии и

(1.7)

для быстрой диффузии.

Нетрудно видеть, что при допустимой для структуры полимеров в трехмерном евклидовом пространстве вариации 2 £ d_f < 3 величина aизменяется в пределах 0¸0,5 для медленной диффузии и 0¸1,0 для быстрой.

С учетом увеличения D_n по мере роста разности температур [Т_с (Т_пл) -Т] (рис.(1.1)) авторы [22] получили взаимосвязь между этими параметрами в следующем общем виде:

D_n = с [Т_с(Т_пл)-Т] ^a, (1.8)

где с - константа.

Как следует из данных рис.1.1, при предполагаемом переходе от медленной диффузии к быстрой, величина D_n » 6,5 или согласно уравнению (1.4)d_f » 2,81. Тогда показатель a в уравнении (1.8) для медленной диффузии равен 0,095, а для быстрой - 0,55. Величины с для этих случае были приняты равными 4,45 и 0,52, соответственно. На рис. 1.2 приведены зависимости D_n от [Т_с (Т_пл) -Т], рассчитанные по уравнению (1.8) при указанных значенияхa и с. Как можно видеть, они хорошо описывают экспериментально полученную вариацию D_n. Это означает, что при [Т_с (Т_пл) - Т] < 120К наблюдается медленная диффузия, а выше этой разности температур - медленная - быстрая [10].

На рис. 1.2 приведена зависимость коэффициента диффузии D_СН4 по метану от температуры стеклования Т_с (плавления Т_пл) для 11 полимеров.

Рис.1.2. Зависимость коэффициента диффузии метана D_СН4 от температуры стеклования Т_с (плавления Т_пл) для 11 полимеров.
Вертикальная штриховая линия указывает величину Т_с, при которой происходит перколяция f_с^фр[10].

 Эта зависимость обнаруживает интересную особенность: до Т_с (Т_пл) » 450К наблюдаются небольшие значения D_СН4, а при Т_с (Т_пл) > 450К начинается быстрый рост коэффициента диффузии. Отметим, что Т_с (Т_пл) » 450К соответствует величине [Т_с (Т_пл) - Т] »157К, т.е., графики рис. 1 и 2 примерно согласуются. Подобная картина зависимости коэффициента диффузии по СО₂ в случае полиэтилена D_СО2 как функции температуры испытаний Т наблюдалась в работах [23,24], где быстрый рост D_СО2 при Т >263К был связан с фрактальными свойствами флуктуационного свободного объема. Как показано в работах [24,25], представление микро полости свободного флуктуационного объема в виде трехмерной сферы является слишком упрощенным и более точно рассматривать эту микро полость как D_o^э - мерную сферу. В такой трактовке объем микро полости V_h^фрдается следующим уравнением:

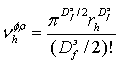(1.9)

где r_h – радиус микро полости свободного объёма.

Если обозначить объем микро полости в трехмерном представлении как V_h , то относительный фрактальный свободный объем f_с^фр можно рассчитать так [10]:

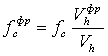_, (1.10)

от Т_с (Т_пл.) показана где относительную долю флуктуационного свободного объема f_с можно принять равной 0,060 для твердофазных полимеров [21].

Для оценки величины V_h существует ряд методов и в работе [10] использован следующий. Экспериментальное значение V_h рассчитывали по формуле [26]:

t₃ = 7,8 V_h - 1,29, (1.11)

где t₃ - время жизни орто- позитрония в экспериментах по аннигиляции позитронов. Величины t₃ приняты для исследуемых полимеров по данным работ [13,27-29]. В уравнении (1.11) t₃ дается в нс, V_h - в нм³ .

Зависимость рассчитанной таким образом величины f_c^фр при условии = D_n на рис.1.3. Как и следовало ожидать, наблюдается увеличение f_c^фрпо мере роста Т_с (Т_пл.) и при Т_с (Т_пл.) ≈ 440К величина f_c^фр_. достигает порога перколяции. Иначе говоря, согласно теории протекания при Т_с (Т_пл.) ≈ 440К, что соответствует [Т_с (Т_пл) - Т] ≈ 147К (сравните с рис.1.1), величина f_c^фр достигает порога перколяции в предположении схемы перекрывающихся сфер (микрополостей), равного 0,34±0,01 [30]. Иначе говоря, согласно теории перколяции при [Т_с(Т_пл) -Т] ≈147К или Т_с(Т_пл.) ≈ 440К в полимерной мембране формируется каркас соединенных между собой микро полостей свободного объема, что облегчает условия диффузии молекул газа-диффузанта и резко повышает коэффициент диффузии [10].

Рис.1.3 Зависимость относительного фрактального свободного объёма f_c^фр, рассчитанного по уравнению (1.10) от температуры стеклования Т_с (плавления Т_пл.). Горизонтальная штриховая линия показывает порог перколяции f_c^фр, равный 0,34±0,01 [10].

 Необходимо дать пояснения относительно абсолютных величин f_c^фр, которые при расчете по уравнению (1.10) могут превышать 1.0, что на первый взгляд представляется физическим абсурдом. На самом деле это означает локальный "всплеск" величины f_c^фр в пределах флуктуации усредненной величины f_c, когда V_h^фр > 16,7V_h. С учетом большого общего количества микро полостей (~10²⁸ м^-3) такой "всплеск" для ограниченного их числа оставляет величину f_c практически неизменным, но может сильно влиять на локальные свойства полимеров на молекулярном уровне.

Следовательно, приведенные выше результаты показали, что в полимерах могут быть реализованы как медленный, так и быстрый процессы диффузии. Переход от первого типа ко второму определяется температурой стеклования (плавления) полимеров, т.е. степенью гибкостей их цепей, и приводит к резкому повышению коэффициента диффузии при одной и той же фрактальной размерности структуры полимера. Применение теории перколяции и фрактального анализа позволило дать структурную трактовку этого изменения - переход от медленной диффузии к быстрому обусловлен образованием свободного перколяционного каркаса перекрывающихся микро полостей флуктуационного свободного объема [10].

Авторы [31] исследовали диффузию кислорода в серии нонборненов с разными Тс и полученных из растворов двумя методами - с быстрым (метод 1) и медленным (метод 2) испарением растворителя. Было обнаружено, что рост коэффициента диффузии с Тс для пленок, полученных методом 1, гораздо сильнее, чем в случае метода 2 (рис. 1.4). Поэтому было сделано предположение, что в пленках с более равновесной структурой (метод 2) реализуется медленная диффузия, а в неравновесных пленках (метод1) - быстрая. Для проверки этого предположения авторы [31] сначала выполнили расчет a согласно вышеприведенной методике [10], затем D_n согласно уравнению (1.8) при цитированных выше значениях коэффициента с и, наконец, величин D _о2 согласно уравнению (1.3). При расчете D отношение (dn/dm) = const = 1,15 для медленной диффузии и (dn/dm) = 1,06¸1,31 для быстрой в силу изменения V_h^фр (V_h= const).

Рис.1.4. Зависимости коэффициента диффузии D _о» по кислороду от разности температур стеклования и испытаний (Тс-Т) в логарифмических координатах для нонборненов. Экспериментальные (1,2) и рассчитанные по уравнению (1,3)(3,4) данные для медленной (1,3) и быстрой (2,4) диффузии [31].

 На рис. 1.4 показано сравнение теории и эксперимента, из которого следует их хорошее соответствие. Следовательно, переход к равновесной структуре полимеров изменяет механизм диффузии газов в полимерах с быстрого на медленный. Более подробно свойства фрактального свободного объема в связи с процессами газопереноса будут рассмотрены в следующем разделе.