Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Фрактальный анализ и синергетика катализа в наносистемах

Нафадзокова Л. Х., Козлов Г. В.,

1.2. Фрактальный свободный объем и диффузия газов в полимерах

В настоящее время предполагается [1,2], что диффузия газов в полимерах реализуется прохождением молекул газа через микро полости свободного объема, который в данном случае является аналогом пористости в кристаллических твердых телах. Однако, для прохождения газа-диффузанта через полимерную мембрану необходимо образование сквозных каналов или, иначе говоря, перколяционного каракаса микро полостей. При этом в случае схемы перекрывающихся сфер порог перколяции равен 0,34±0,01 [30], что намного больше максимально возможной величины относительного свободного объема f_c , равной 0,159 [32], для полимеров. Это кажущееся расхождение имеет два альтернативных объяснения. В классических моделях процесс диффузии рассматривается как последовательность перескоков молекул газа-диффузанта от одной микро полости свободного объема к другой, которые образуются и исчезают вследствие тепловых флуктуаций. При этом указанные микро полости моделируются трехмерной сферой, что исключает достижение величиной f_cпорога перколяции [33]. Однако моделирование микро полости как трехмерной сферы с гладкими стенками далеко от реальности [34]. Стенки микро полости представляют собой поверхность сегментов макромолекул, колеблющихся вокруг своих равновесных положений [35]. Поэтому авторы [24,25] предложили моделировать указанную микро полость D_f - мерной сферой, что является основным постулатом фрактальной концепции свободного объема. Как показано выше в такой трактовке величина f_c^фр может достигать порога перколяции и это условие является граничным для реализации процессов быстрой и медленной диффузии в полимерах [10]. Авторы [36,37] продемонстрировали реальность фрактального свободного объема в полимерах, используя общие модели динамики фрактальных структур [38] и экспериментальные данные по зависимости коэффициента диффузии от температуры [39], которые для диффузии двуокиси углерода в полиэтилене высокой плотности ПЭВП были получены согласно уравнению аррениусовского типа [39]:

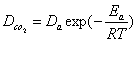(1.12)

где D_{СО2 -} коэффициент диффузии по двуокиси углерода, D_o - константа, Е_а - энергия активации диффузии, R - универсальная газовая постоянная, T - температура испытаний

Стенли [38] рассмотрел фундаментальные законы диффузии, и переноса для сред, представляющих собой случайную смесь компонент А и В, в которой имеются хорошо и плохо проводящие участки. Очевидно, конкретизация этой общей модели для диффузии газов в полимерах выглядит так: полимер рассматривается как случайная смесь свободного объема А (проводник) и собственно полимерного материала (макромолекул, занятый объем) В (изолятор), имеющего нулевой коэффициент диффузии. Это так называемая случайная сетка резисторов (ССР) или предел "муравья"[38]. В пределе ССР большая проводимость полагается равной единице, меньшая - равная нулю. При приближении концентрации компоненты А, т.е., f_c ^фр к порогу протекания р_с сверху (р_с = 0,34 ± 0,01 [30]) макроскопическая проводимость å стремится к нулю, и ее поведение описывается критическим показателемm [38]:

å ~ (f_c ^фр - р_с ) ^m. (1.13)

Для случая f_c ^фр_.< р_с используется предел случайной сверхпроводящей сетки (ССС), где меньшая проводимость равна единице, а большая проводимость бесконечна. При приближении к р_с снизу проводимость стремится к бесконечности по закону [38]:

. (1.14)

Величина макроскопической проводимости связана с коэффициентом диффузии D соотношением Нернста-Эйнштейна:

, (1.15)

где n – плотность носителей заряда.

Рассмотрим конкретную форму соотношения между Σ и D. Диффузионный поток представляет собой количество поверхности А за единицу времени t [33]:

. (1.16)

В стационарном режиме диффузии величину g можно определить так [33]:

, (1.17)

где с₁ и с₂ – концентрации диффузанта на наружной и внутренней поверхности полимерной мембраны, соответственно, – толщина этой мембраны.

В режиме стационарной диффузии с₁ = const., = const.,A = const. и для t = const. из уравнений (1.16) и (1.17) получим [36]:

, (1.18)

или

. (1.19)

Далее из соотношений (1.15) и (1.19) получим:

. (1.20)

Показатели μ и s в соотношениях (1.13) и (1.14), соответственно, определяются следующим образом. Величина μ даётся так [38]:

(1.21)

где ν_n – критический индекс перколяции, равный 0,80¸0,88 [30,40,41], d – размерность евклидова пространства, в котором рассматривается фрактал (d = 3), d_w – размерность траектории случайного блуждания на фрактале.

Величину d_f можно рассчитать согласно уравнению [42]:

, (1.22)

где j_{кл -} относительная доля областей локализации порядка (кластеров), S - площадь поперечного сечения макромолекулы (для ПЭВП S = 18,7A^°2 [43]), с_¥ - характеристическое отношение, которое является показателем статистической гибкости полимерной цепи [44] и равно 5,8 для ПЭВП [45].

В свою очередь, величину j_кл как функцию Т можно рассчитать так [45]:

j_{кл =} 0,03 (1-К) (Т_пл - Т)^0,55, (1.23)

где К - степень кристалличности, Т_пл - температура плавления.

Согласно правилу Аарони-Штауффера размерность d_w определяется следующим образом [38]:

(1.24)

Рис.1.5. Зависимость фрактального флуктуационного свободного объёма _. от температуры Т для ПЭВП. Штриховая горизонтальная линия указывает величину порога перколяции р_с [25].

 Показатель S можно рассчитать из уравнения [38]:

(1.25)

где d_u – размерность неэкранированного периметра фрактального объекта, равная [47]:

(1.26)

На рис.1.5 приведена зависимость фрактального флуктуационного свободного объёма от температуры Т для ПЭВП [25]. Как можно видеть, величина f^фр._с. может быть существенно выше предельного значения f_c в классической трактовке (0,159 [32]) и при Т≈270К достигает порога перколяции (сравните с данными рис.1.3). Далее согласно соотношениям (1.13) и (1.14) можно определить величину Σ выше и ниже порога перколяции, т.е., выше и ниже Т = 270К, и затем согласно соотношению (1.20) рассчитать коэффициент диффузии D^T в относительных единицах.

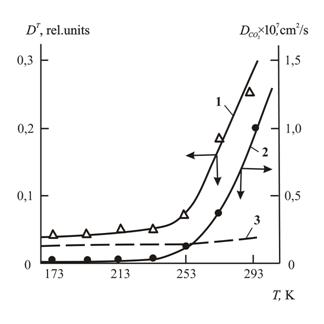
Рис.1.6. Зависимости коэффициентов диффузии D^T и, рассчитанных согласно соотношениям (1.13), (1.14)(1) и (1.12)(2), соответственно от температуры Т для ПЭВП. Кривая 3 показывает зависимость D^T(Т), рассчитанную по соотношению (1.14) с использованием f_c [36].

На рис.1.6 приведено сравнение температурных зависимостей D^T, рассчитанной указанным способом, и, рассчитанной согласно уравнению (1.12). Как можно видеть, наблюдается полная симбатность зависимостей D^T (T) и (T), что указывает на реальность фрактального свободного объёма для полимеров. Кроме того, на рис.1.6 приведена зависимость D^T(T) (кривая 3), рассчитанная по соотношению (1.14) в предположении, что величина f_c изменяется в пределах 0,060÷0,110, т.е., как предполагают классические теории свободного объёма [1,2]. Как можно видеть, в этом случае увеличение D^T в интервале Т = 173÷293К составляет ~10%, что явно не соответствует экспериментальным данным [37].

Приведенные на рис.1.5 величины достигают ~0,55 и в принципе могут быть больше 1,0 (см. рис.1.3), что на первый взгляд представляется физическим абсурдом. Однако если рассматривать формулу (1.10) для оценки , то очевидно, как уже отмечалось выше, что речь идёт о локальном увеличении объёма микро полости по сравнению с предполагаемыми классическими моделями свободного объёма. Собственно говоря, такая локализация процесса диффузии предполагалась и ранее Аналогичный локальный «всплеск» ангармонизма предположил в своей концепции разрушения полимеров Журков [48]. Если учесть, что понятия свободного объёма и ангармонизма тесно связаны [21,49], то предположение локального роста свободного объёма представляется вполне оправданным [37].

Следовательно, рассмотренные выше результаты показали возможность описания температурной зависимости коэффициента диффузии в рамках общей модели случайных смесей с привлечением концепции случайного свободного объема. Отметим, что хотя в работах [36,37] соответствие получено только для одного полимера (ПЭВП) и одного газа-дифффузанта (СО₂), использование общих уравнений (1.12), (1.13), (1.14),(1.22) и (1.23) предполагает аналогичное соответствие для любых пар газ-полимер[36].

Нигматуллин предположил [50], что ряд физических систем, которые могут быть описаны уравнениями в дробных производных, должны содержать в себе каналы, входящие в состав некоторой фрактальной структуры. Структура собственно каналов переноса может быть различной и порождаться определенной фрактальной структурой среды. В этом случае дробный показатель соответствует относительной доле каналов, открытых для протекания (диффузии) [50].

К указанным физическим системам с полным основанием следует отнести и полимеры при температурах ниже их температуры стеклования (плавления). Как известно [51,52], такие полимеры обладают фрактальной структурой. Кроме того, полагается [1,2,39], что процессы диффузии в них реализуются через микро полости свободного объёма, совокупность которых и формирует каналы диффузии. Очень важно, что относительная доля флуктуационного свободного объёма f_c связана с фрактальной размерностью структуры d_f соотношением [53]:

(1.27)

Исходя из сказанного выше, можно предположить, что для полимеров дробный показатель ν_∂p будет определенным образом связан с параметрами флуктуационного свободного объёма и авторы работы [54] предприняли попытку выяснения физического смысла этой взаимосвязи, что было сделано на примере аморфно-кристаллического ПЭВП.

Ранее было показано [55], что относительная доля флуктуационного свободного объема f_c в случае аморфно-кристаллических полимеров может быть определена следующим образом:

(1.28)

где j_р.м. - относительная доля рыхло упакованной матрицы аморфной фазы, определяемая из уравнения [53]:

j_р.м. = 1-К - j_кл. (1.29)

По мере роста температуры испытаний общей тенденцией для полимеров является как рост d_f вследствие термофлуктуационного распада кластеров [53,56], так и увеличение коэффициента диффузии D[1,2]. Это предполагает повышение доли каналов диффузии и, согласно [50], увеличение ν_∂p. В работе [54] использована структурная трактовка дробного показателя, согласно которой [57]:

(1.30)

Нетрудно видеть, что в этом случае аналогично работе [50] ν_∂p представляет собой дробную часть фрактальной размерности, которая несёт основную информацию о структуре полимера [58]. На рис.1.7 приведена зависимость f_c(ν_∂p) для ПЭВП, которая показала увеличение f_с, т.е., доли каналов диффузии по мере роста ν_∂p (или d_f). Экстраполяция линейной зависимости f_c(ν_∂p) к предельной величине ν_∂p = 0,95 [20] даёт f_c = 0,113, что и ожидалось согласно концепции Симхи-Бойера [59]. Экстраполяция к f_c = 0 даёт ν_∂p ≈0,52 или d_f = 2,52. Указанная величина d_f соответствует квазиравновесному состоянию структуры полимеров, для которых повышение доли кластеров φ_кл полностью сбалансировано энтропийным натяжением полимерных цепей [60]. Более подробно этот аспект будет рассмотрен ниже.

Рис.1.7. Зависимость относительного флуктуационного свободного объёма f_c от дробного показателя ν_∂pдля ПЭВП [54].

 Как известно[14,15], величина коэффициента диффузии зависит не только от интегральной величины f_c, но и от локальной – диаметра микро полостей свободного объёма или, точнее, от отношения диаметров этой микро полости и молекулы газа-диффузанта d_n/d_м (см. уравнение (1.3)). Объем указанной микро полости можно рассчитать согласно уравнению (1.11), а также альтернативным методом [61]:

(1.31)

где n - коэффициент Пуассона, k - постоянная Больцмана. Т_с - температура стеклования (или плавления), Е - модуль упругости.

Затем, моделируя микро полость трехмерной сферой, можно рассчитать ее диаметр d_n из чисто геометрических соображений. На рис. 1.8 приведена зависимость d_n (ν_∂p), которая показала линей рост d_n по мере увеличения ν_∂p. Экстраполяция d_n к нулю вновь дает ν_∂p » 0,52 или d_f ≈ 2,52.

Следовательно, данные рис. 1.7 и 1.80 предполагают увеличение доли и размеров (интегральной и локальной характеристик) каналов диффузии по мере увеличения ν_∂p.

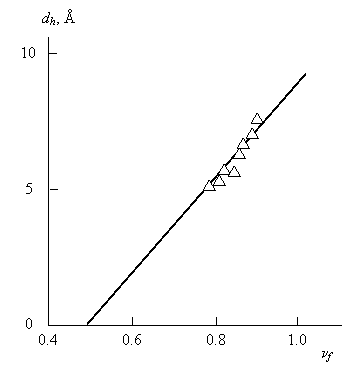
Рис.1.8. Зависимость диаметра d_n микро полости свободного объёма от дробного показателя ν_∂p для ПЭВП [54].

 Это обстоятельство позволяет построить зависимость коэффициентов диффузии по неону (D_Ne) и метану () от произведения ν_∂pd_h, которые приведены на рис.1.9. Обе зависимости линейны, наблюдается рост D по мере увеличения произведения ν_∂pd_h, но особого внимания заслуживает экстраполяция этих прямых к D = 0, которая даёт конечные значения ν_∂pd_h, равные 2,10 и 3,90Å для Ne и СН₄, соответственно. При ν_∂p=0,52 это соответствует d_h = 4,04 и 7,40Å для диффузии указанных газов. Если принять величины d_м в случае их самой неблагоприятной для диффузии ориентации в микро полости (d_м = 2,4Å для Ne [11] и 4,2Å для СН₄ [12]), то получим отношения d_n/d_м, равные 1,68 и 1,78, соответственно. Как известно [19] , при d_n/d_м £ 1,7 происходит изменение механизма, т.е., такие, при которых происходит переход от структурного механизма диффузии от структурного к молекулярному, причем последний характеризуется интенсивным взаимодействием стенок микро полости и молекулы газа-диффузанта.

Рис.1.9.Зависимость коэффициентов диффузии по неону D_Ne (1) и метану D_CH4 (2) от величины произведения ν_∂pd_h для ПЭВП [54].

 Следовательно, величины ν_∂pd_h при экстраполяции к D=0 можно записать как , где -дробный показатель для квазиравновесного состояния структуры, равный в случае ПЭВП ~0,52. Тогда, согласно данным рис.1.9 зависимость D от параметров ν_∂p и d_h можно записать так:

(1.32)

где с – константа, равная 29 и 2 для Ne и СН₄, соответственно.

На рис.1.10 приведено сравнение экспериментальных и рассчитанных согласно уравнению (1.32) зависимостей коэффициента диффузии от температуры испытаний для Ne и СН₄. Как можно видеть, получено достаточно хорошее как качественное, так и количественное соответствие теории и эксперимента.

Следовательно, процесс диффузии в ПЭВП может быть описан с использованием дробного показателя , определяемого согласно интерпретации, соответствует структурной трактовке ПЭВП в рамках уравнению (1.30). В этом случае величина  имеет чёткую физическую интерпретацию доли каналов структуры, открытых для диффузии [50]. Эта фрактального анализа. Отметим, что термин «открытые для диффузии каналы» соответствует структурному механизму диффузии (d_n/d_м>1,7 [18]), когда отсутствует взаимодействие газ-полимер.

Рис.1.10.Сравнение экспериментальных (1,2) и рассчитанных согласно уравнению (1.32) (3,4) температурных зависимостей D_Ne (1,3) и D_СН4 (2,4) для ПЭВП[54].

В то же время дробный показатель, определенный в рамках теории дробного дифференцирования [9], не может быть корректно использован в предложенной трактовке, поскольку она дает снижение  (или a) по мере увеличения d_f [54]. Тем не менее, в разделе 1.1 показано применимость a для описания медленной и быстрой диффузии в полимерах. Это наблюдение указывает, что для конкретного полимера на существует однозначного дробного показателя, а его величина определяется как структурой полимера, так и процессом (эволюцией), в котором он участвует [54].