
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
1.3. Мультифрактальные модели диффузии газов в полимерах.
В настоящее время хорошо известно [39], что величина коэффициента диффузии D для полиэтилена скачкообразно изменяется при его температуре плавления Тпл. Этот эффект получил объяснение с позиции разных теоретических концепций. Так, в работе [39] этот скачок объяснен со структурных позиций, а именно исчезновением кристаллитов при Тпл. С позиции кластерной модели структуры аморфного состояния полимеров указанный скачок объяснен распадом "замороженного" локального порядка в аморфной фазе полиэтиленов при Тпл [14,15]. И наконец, с позиции фрактального анализа этот скачок объяснен изменением структуры полиэтилена от фрактальной (твердофазное состояние) к евклидовой (расплав) [18].
Однако существует еще один фундаментальный аспект проблемы, которому до сих пор не уделялось должного внимания. Наличие этого аспекта хорошо вытекает из двух хорошо известных экспериментальных наблюдений: зависимости величины D для одного и того же полимера от размера (диаметра) молекул газа-диффузанта dm [1,33] и резко отличающейся степени этой зависимости для аморфно-кристаллического полиэтилена и его расплава [39]. В последнем случае зависимость D(dm) выражено гораздо слабее, чем в первом. Эти наблюдения позволяют сделать следующее предположение. В аморфно-кристаллическом полиэтилене существует типичное для полимеров распределение размеров микро полостей свободного объема dh [24,25].Такое распределение (или мультифрактальность) микро полостей свободного объема является следствием мультифрактальности структуры полимера [62]. Если исходить из приближенного условия реализации диффузии dm £ dh , то это означает, что по мере роста dm в аморфно-кристаллическом полимере остается все меньше микро полостей с размером dh, соответствующих условию диффузии, и это резко снижает величину D. Расплав полиэтилена является евклидовым объектом, для которого характерно монодисперсное распределение dh и это нивелирует различия в диффузии молекул газов-диффузантов с разными dm. Авторы [63,64] выполнили проверку корректности сделанного выше предположения на примере диффузии разных газов через аморфно-кристаллический полиэтилен и его расплав.
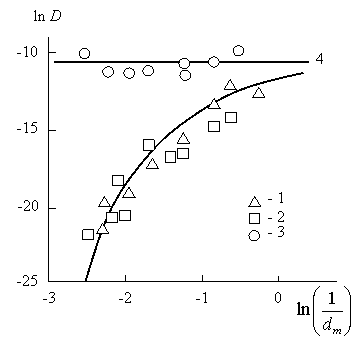
Рис.1.11. Зависимость коэффициента диффузии D от обратной величины диаметра молекулы газа-диффузанта dm в двойных логарифмических координатах для аморфно-кристаллического полиэтилена (1,2) и его расплава (3,4). Расчет: по уравнениям (1.12) (1,3), (1.3)(2) и (1.38)(4)[64].
На рис. 1.11 показана зависимость D(1/ dm) для диффузии 9 газов [39] в случае аморфно-кристаллического полиэтилена и его расплава в двойных логарифмических координатах, где значения Dопределены согласно уравнению (1.12). Как можно видеть, эта зависимость резко различается для двух указанных состояний полимера: если для аморфно-кристаллического ПЭВП наблюдается сильный спад Dпо мере роста dm, то для расплава эта зависимость практически отсутствует. Поскольку зависимость D(1/dm) для аморфно-кристаллического полимера криволинейна, то это означает изменение показателя 2(Df э- ds) / ds в уравнении (1.3) по мере вариации масштаба измерения dm или, с учетом условия ds = const, изменение размерности Df э.
зависимость D (1/dm) прямолинейными отрезками, из их наклона можно рассчитать величину показателя 2(Df э - ds) / ds, затем размерность Df э и по уравнению (1.4) - величину df для каждого такого участка. На рис. 1.12 показана зависимость df(dm), из которой следует рост df по мере увеличения dm или увеличения масштаба измерения. Это является типичным признаком мультифрактальности структуры аморфно-кристаллического ПЭВП [58].

Рис. 1.12. Зависимость фрактальной размерности df структуры ПЭВП от масштаба измерения dm для аморфно-кристаллического состояния. Штриховая линия указывает максимальную величину df = d =3 [64].
Отметим, что исходя из данных рис. 1.11 и уравнения (1.4), аналогичную диаграмму можно построить и для Df. Это означает мультифрактальность свободного объема в аморфно-кристаллическом ПЭВП, которая является следствием мультифрактальности структуры этого полимера (рис.1.12). Рис. 1.12 показывает снижение df по мере уменьшения масштаба dm, т.е., увеличение плотности структуры с уменьшением масштаба [65]. Это по существу является определением фрактала по соотношению [20]:
r ~ Rg df- d , (1.33)
где r - плотность фрактального объекта, Rg - его радиус инерции.
Число микро полостей Nh размером dh можно оценить из соотношения [64]:
Nh ~ dh- df. (1.34)
Если предположить, что Nh соответствует относительной доле микро полостей размером dh , то можно (после соответствующего нормирования величин Nh) построить распределение dh, показанное на рис. 1.13. Как следует из этого рисунка, вероятность Рh (равная относительной доле микро полостей с размером ³ dh) обнаружения микро полости с размером больше dh быстро снижается по мере роста dh. Так, вероятность обнаружения микро полости с dh » 12А° равна 0,001.

Рис. 1.13. Зависимость величины Рh обнаружения микрополости свободного объема размером dh от величины dh для аморфно-кристалличес-кого ПЭВП.[64].
Теперь, рассмотрим зависимость D (1/ dm) для расплава ПЭВП, также показанную на рис. 1.11. В первом приближении ее наклон равен нулю и это означает следующее условие [63]:
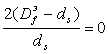 (1.35)
(1.35)
или Df э = ds. Для фрактальных объектов ds £ 2 [66], а минимальная величина df = 2 [42]. Из уравнения (1.4) следует, что минимальное значение Df э также равно 2. Определить величину ds можно из следующего уравнения [66]:
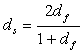 (1.36)
(1.36)
Уравнение (1.36) предполагает вариацию ds = 1.33 ¸ 1.50 при максимально возможной вариации df (2£df < 3 [42]). Таким образом, нельзя получить условие (1.35) в предположении фрактальности расплава ПЭВП. Поэтому следует предположить, что расплав является евклидовым объектом, в котором размерность Df теряет смысл. С формальной точки зрения это следует из уравнения (1.4): при df = d величина Df э ®¥. Со скоростных позиций это означает следующее: размерность Df э характеризует степень энергетической возбужденности рыхло упакованных областей полимера. В расплаве отсутствуют и кристаллиты, и "замороженный" локальный порядок, вследствие чего нет необходимости отдельной характеристики разных структурных компонент. Весь расплав характеризуется размерностью d =3. Для евклидовых объектов справедливо тождество [67]:
ds = df = d =3. (1.37)
Поэтому условие (1.35) для евклидовых объектов выполняется тривиально при замене Df э на df = d [64].
Следовательно, исходя из вышесказанного, уравнение (1.3) в случае расплава принимает вид [64]:
D = Do¢fc , (1.38)
где величину fc можно принять согласно Бойеру [59] равной ~0,113. Следовательно, для расплава ПЭВП D c точностью до константы равен Do ¢ и постоянен. Величина Do¢ в этом случае равна 2,45х 10-4 см2/с, что близко к теоретической величине DoТ [39]:
![]() (1.39)
(1.39)
рассчитываемой исходя из предположения о скачке молекулы газа-диффузанта на расстояние l в несколько ангстрем с частотой n = 1012 ¸1013 Гц. Рассчитанная по уравнению (1.38) величина D при указанных выше значениях констант Do¢ и fc показана на рис.1.11 штриховой линией. Теоретический расчет хорошо согласуется с экспериментальной зависимостью и это означает отсутствие мультифрактальности (распределения) размеров микро полостей свободного объема в расплаве, что как отмечалось выше, является следствием потери структурой полимера фрактальных свойств [63].
Зависимость рассчитанного по уравнению (1.3) параметра Do¢ для аморфно-кристаллического ПЭПВ показано на рис.1.14. Как следует из приведенных данных, наблюдаются большие значения Do¢ (порядка 10-5 см2/с) только для двух инертных газов с наименьшим размером молекул (He иNе), а для остальных газов-диффузантов величина Do¢ примерно постоянно и имеет порядок 10-9 см2/с. Это дает возможность теоретической оценки коэффициента диффузии D для аморфно-кристаллического ПЭВП по уравнению (1.3) при следующих условиях: Do¢ = 2х10-9 см2/с, fc »0,07, ds = 1,45, dn= 12 Å и величины Df принимались в интервале 4,06¸9,78 согласно их оценке из наклона линейной аппроксимации отдельных участков криволинейной зависимости D (1/dm) на рис.1.11. Сравнение теории и эксперимента, показанное на рис.1.11, продемонстрировало их хорошее соответствие, за исключением данных для He и Ne по указанной выше причине. Следовательно, соответствие теории и эксперимента для аморфно-кристаллического ПЭВП достигается при учете зависимости df (или Df) от масштаба измерения dm и включения в расчетную схему этих масштабов (dm и dh), что однозначно указывает на мультифрактальность структуры (и, следовательно, свободного объема) этого полимера. Для получения соответствия теории и эксперимента в случае расплава ПЭВП, который является евклидовым объектом, учет вышеуказанных условий не требуется. Отметим также, что размерность df = 2.67 соответствует вероятности Рh » 0,84. Это означает, что величина df в монофрактальном представлении структуры аморфно-кристаллического ПЭВП должна быть близка к указанному значению df. Оценки величины df для полиэтиленов независимыми способами подтверждают это предположение [68,69].
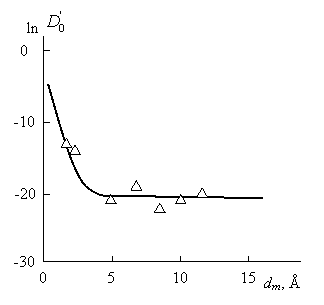
Рис.1.14. Зависимость константы Do¢ от диаметра молекул газа-диффузанта dm для аморфно-кристаллического ПЭВП в логарифмических координатах [64].
Далее можно построить мультифрактальную диаграмму для структуры аморфно-кристаллического ПЭВП в терминах a- f, где a- скейлинговый показатель, характеризующий концентрацию сингулярностей, f– размерность сингулярностей a [70]. Для этой цели, авторы [63,64] использовали простейший вариант [71]:
Рi » e ia i, (1.40)
где Рi – вероятность обнаружения микро полости с относительным размером e i.
Величина Рi принята равной Рh (рис.1.13), а eI определена из построения множества («пыли») Кантора следующим образом. Из данных рис.1.13 следует, что интервал вариации dh можно принять равным 0¸12Å. Тогда величина dm должна нормироваться на величину интервала вариации dh,, т.е., 12Å. Далее в построении Кантора из первоначального отрезка длиной 1 удаляется средняя его часть (одна треть) и тогда длина двух оставшихся частей будет равна ~ 0,667 [70,72]. Затем эту величину следует разделить пропорционально размеру между поверхностями соседних микро полостей и размеру микро полости свободного объема при условии dh = dm и последняя из указанных частей соответствует ei [72,73]. Величина f рассчитывается следующим образом [72]:
f = df – 2. (1.41)

Рис.1.15. Мультифрактальные диаграммы структуры аморфно- кристаллического ПЭВП (1) и его расплава (2) (тривиальный случай) в координатах a - f [64].
Построенная указанным способом диаграмма a - f для аморфно-кристаллического ПЭВП показана на рис.1.15. Здесь также приведена диаграмма a - f для расплава ПЭВП (тривиальный случай), которая является прямой с ординатой f = 1 (df = d =3), параллельной оси a. Диаграмма a-f для аморфно-кристаллического ПЭВП имеет куполообразную форму, типичную для таких диаграмм [62,70-73]. Ее физический смысл заключается в следующем: кривая a - f показывает вероятность обнаружения в полимере микро полости с размером больше произвольного dh при произвольной df[63.64].
Следовательно, приведенные выше данные экспериментально подтвердили мультифрактальную природу структуры (и, как следствие, свободного объема) аморфно-кристаллического ПЭВП и позволили получить оценку его мультифрактальных характеристик на основе диффузионных свойств этого полимера. Аналогичные результаты были получены авторами [74,75] для поливинилацетата.Такой подход позволяет также построить кривую распределения размеров микро полостей свободного объема. Диаграмма a-f в обычных (уже классических) координатах мультифрактального формализма показывает вероятность существования в полимере микро полостей с размером больше любого фиксированного их диаметра dh[63.64.74.75]. Расплав полиэтилена является евклидовым объектом с монодисперсным распределением размеров микро полостей. Указанные обстоятельства определяют различную форму зависимостей коэффициента диффузии D от размера молекул газа-диффузанта [63,64].
Еще одна количественная мультифрактальная модель, позволяющее прогнозирование коэффициента диффузии как функции размера молекул газа-диффузанта, предложена в работе [76]. Выше было показано, что в аморфно-кристаллических полимерах в процессе диффузии участвует не вся аморфная фаза, а только та ее часть которая содержит микро полости функционального свободного объема с диаметром dh, отвечающем условию dh ³dm , т.е., те микро полости, которые допускают диффузию молекул газа-диффузанта диаметром dm. Доля такой доступной для диффузии аморфной фазыaамдост определяется следующим образом [77]:
aамдост = aам dm, (1.42)
где aам - объемное содержание аморфной фазы в аморфно-кристаллическом полимере.
По своему физическому смыслу параметр aамдост соответствует вероятности Рh обнаружения в полимере свободного объема диаметром dh ³ dm. В рамках мультифрактального анализа величина Рh(dm) в первом приближении может быть определена следующим образом [71]:
Рh(dm) = dm –df, (1.43)
где df – фрактальная размерность структуры полимера, равная для аморфно-кристаллического ПЭВП 2,75 [18,68,69].
Кроме того, при расчете aамдост по уравнению (1.42) следует обратить внимание на следующее обстоятельство. В настоящее время предполагается [33], что в аморфно-кристаллическом полимере кристаллические области непроницаемы для диффузии газов и тогда:
aам = 1- К. (1.44)
Однако, в рамках кластерной модели было продемонстрировано [14,15], что области локального порядка (кластеры) также непроницаемы для диффузии газов и в этом случае величина aам = jр.м. определяется согласно уравнению (1.29).

Рис. 1.16. Зависимость доступной для диффузии доли аморфной фазы aамдост , выраженной как параметры (1- К)dm (1), (1- К - jкл) dm (2) и Рh (3) от диаметра молекулы газа диффузанта dN для ПЭВП [76].
На рис. 1.16 приведено сравнение зависимостей aамдост, где aам определена по уравнениям (1.29) и (1.44) и Рh от dm Как и следовало ожидать, в силу определения aамдост и Рh степенной зависимостью, наблюдается быстрый спад этих параметров по мере роста dm.
Величина Рh по абсолютной величине является промежуточной между значениями aамдост, определенными указанными выше способами, что позволяет использовать эту вероятность для характеристики доли аморфной фазы для диффузии газов. Тогда уменьшение коэффициента диффузии D твердофазного ПЭВП по сравнению с его расплавом будет определяться вероятностью Рh (dm), что аналитически можно выразить следующим образом [76]:
D = Dам Рh, (1.45)
где Dам – коэффициент диффузии полностью аморфного полиэтилена, т.е., его расплава.
В табл.1.1 приведены значения dm для 23 газов, величины Рh и Dам, рассчитанные по уравнениям (1.43) и (1.3), соответственно, а также экспериментальные значения Dэкс [11,12] и рассчитанные по уравнению (1.45) Dтеор величины коэффициента диффузии для ПЭВП. Как можно видеть, получено достаточно хорошее значение величин Dэкс и Dтеор, подтверждающее предложенную в работе [76] вероятностную (мультифрактальную) модель диффузии газов в полимерных мембранах.
В табл.1.1 также приведены экспериментальные значения коэффициента диффузии 12 газов для полидиметилсилоксана (ПДМС) [11]. Интересно отметить хорошее соответствие величин Dам, что предполагает, исходя из уравнения (1.45), Рh (dм) = 1,0. Такой результат также согласуется с предложенной выше моделью, поскольку для монофрактальной структуры каучукообразного ПДМС микро полости свободного объема имеют одинаковый размер (принятый здесь dh2 12Å [13]) и поэтому Рh (dм) = 1,0.
Приведенные в табл.1.1 экспериментальные значения коэффициента диффузии для полиизопрена (ПИ) имеют такую же тенденцию изменения этого параметра при вариации dm, как и для ПЭВП и ПДМС, но абсолютные значения Dэкс существенно (в несколько раз) ниже, чем для ПДМС, хотя оба полимера находятся в каучукообразном состоянии. Объяснить это различие также можно в рамках рассматриваемой модели. Поскольку ПДМС является слабо сшитым каучуком [11], то для него, как и для линейного ПЭВП, в уравнении (1.3) можно принять ds=1,0 [17]. Однако, для более плотно сшитого каучука ПИ такая аппроксимация уже не верна. Для сшитых (или разветвленных) макромолекул ds=1,0¸1,33 [17]. Поскольку каучуки не сшиваются слишком плотно, чтобы они не теряли эластичность, то можно предположить, что ПИ имеет промежуточную между слабо сшитым ПДМС и плотно сшитыми стеклообразными эпоксиполимерами плотность сшивки и, как следствие, промежуточную величину ds, которая в работе [76] принята равной 1,20. Изменение ds от 1,0 до 1,20 приводит к снижению показателя 2(df - ds)/ ds в уравнении (1.3) от 3,90 до примерно 2,40. В свою очередь это приводит к уменьшению Dам при прочих равных условиях. Приведенное в табл.1.1 сравнение величин Dэкс и Dтеор для ПИ показало их хорошее соответствие, т.е., предложенная в работе [76] модель количественно описывает это расхождение величин D для ПДМС и ПИ.
Следовательно, рассмотренная выше вероятностная (мультифрактальная) модель диффузии газов в полимерных мембранах имеет простой и ясный физический смысл и позволяет достаточно точное прогнозирование коэффициента диффузии разных газов. Отметим, что для этого требуется минимальный набор структурных характеристик (К, df , ds и dh)[76].
Авторы [77] модифицировали рассмотренную выше мульфрактальную модель и использовали ее для прогнозирования коэффициента диффузии ряда стеклообразных полимеров. Основанием для модификации модели [76] послужило, следующее обстоятельство. Оценки согласно уравнениям (1.3), (1.43) и (1.45) для ряда стеклообразных полимеров (поли-4-метилпентен, полистирол, поликарбонат, поливинилтриметилсилан, полисульфон, полифениленоксид) дали завышенные величины D по сравнению с их экспериментальными значениями [77]. Это обусловлено меньшими величинами dhдля указанных стеклообразных полимеров и соответствующим изменением механизма газопереноса.
Таблица 1.1
Расчетные и экспериментальные характеристики диффузии газов в полимерах [76].
| Газ | dм,Å | Dам´107, см2/с | Рh | ПЭВП | ПДМС | Полиизопрен | ||
| Dтеор´107, см2/с | Dэкс´107, см2/с | Dэкс´107, см2/с | Dтеор´107, см2/с | Dэкс´107, см2/с | ||||
| Не | 1,82 | 671 | 0,193 | 129 | 70 | 370 | 123 | 216 |
| Ne | 2,25 | 293 | 0,108 | 32 | 23 | 250* | 65 | 77,4* |
| Ar | 3,0 | 196 | 0,049 | 4,7 | 3,7 | 108 | 27 | 13,6 |
| Kr | 3,20 | 74 | 0,041 | 3,0 | 1,8 | 67 | 23 | 7,2* |
| Xe | 3,55 | 50 | 0,031 | 1,5 | 0,7 | 45 | 20,4 | 2,7* |
| Rn | 3,70 | 42 | 0,027 | 1,2 | 0,24* | 26 | 14,6 | 1,2* |
| H2 | 2,22 | 309 | 0,112 | 35 | 35* | 330 | 68 | 109* |
| O2 | 3,0 | 96 | 0,053 | 5,1 | 4,6 | 115 | 27 | 17,3 |
| N2 | 3,15 | 73 | 0,043 | 3,1 | 3,2 | 94 | 22 | 11,3 |
| CO2 | 3,23 | 72 | 0,040 | 2,9 | 3,7 | 85 | 18 | 13,5 |
| CO | 3,23 | 72 | 0,040 | 2,9 | 3,3 | 98* | 22 | 12,5 |
| CH4 | 3,30 | 66 | 0,038 | 2,5 | 1,90 | 77 | 20 | 8,9 |
| Этан | 4,06 | 29 | 0,022 | ,65 | 0,68 | - | 11 | 4,0 |
| Пропан | 4,76 | 16 | 0,014 | ,22 | 0,32 | - | 6,8 | 2,1 |
| Н-Бутан | 5,66 | 13 | 0,012 | ,16 | 0,20 | - | 2,6 | 1,6 |
| Этилен | 3,82 | 36 | 0,025 | 0,90 | 1,02* | - | 6,7 | 4,3* |
| Пропи лен | 4,63 | 18 | 0,013 | 0,26 | 0,58 | - | 4,2 | 3,0 |
| 1-октен | 5,36 | 23 | 0,010 | 0,23 | 0,33* | - | 2,9 | 1,5* |
| Ацети лен | 3,70 | 98 | 0,027 | 2,66 | 1,40* | - | 7,2 | 5,7* |
| Метил Ацети лен | 4,62 | 46 | 0,029 | 1,33 | 0,97* | - | 4,2 | 4,1* |
| Этилацети Лен | 5,26 | 38 | 0,025 | 0,94 | 0,68* | - | 3,1 | 2,9* |
| Аллен | 5,38 | 45 | 0,029 | 1,30 | 1,05 | - | 4,8 | 5,0 |
| Бутадиен | 5,45 | 36 | 0,025 | 0,90 | 0,80* | - | 4,6 | 3,4* |
*Рассчитаны по методике [11]
Как показано выше, при dm<1,7dh реализуется структурный механизм газопереноса, контролируемый размерностью df. При dm ³1,7dh реализуется взаимодействие молекул газа-диффузанта со стенками микро полости свободного объема, чья размерность равна размерности областей локализации избыточной энергии Dэf и тогда контролирующей процессы газопереноса размерностью является Dэf (молекулярный механизм). Соответственно уравнение (1.43) следует модифицировать следующим образом [77]:
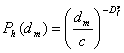 , (1.46)
, (1.46)
где с- константа, равная 1Å, которая вводится для согласования обеих частей уравнения (1.46). Аналогичная константа должна быть и в уравнении (1.43).
Далее, используя литературные значения dм для двух газов (H2 и СН4), можно рассчитать величины Dтеор в случае указанных выше стеклообразных полимеров (для поли-4-метилпентена принята степень кристалличности К = 0,40). На рис. 1.17 приведено сравнение экспериментальных Dэкс и рассчитанных указанным способом Dтеор коэффициентов диффузии в логарифмических координатах. Как можно видеть, получено достаточно хорошее соответствие теории и эксперимента, что вновь указывает на корректность предложенной мультифрактальной модели для любого состояния полимеров [77].
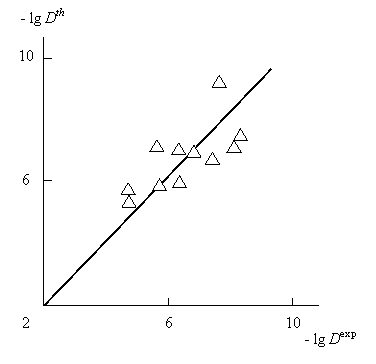
Рис.1.17. Сравнение экспериментальных Dэкс и рассчитанных согласно уравнениям (1.3), (1.45) и (1.46)Dтеор коэффициентов диффузии в логарифмических координатах для 6 стеклообразных полимеров и 2 газов [77].
