
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
Расстояния. Теорема Пифагора
Сведения из теории
Для прямоугольного треугольника с катетами a, b и гипотенузой с имеет место теорема Пифагора: сумма квадратов катетов равна квадрату гипотенузы. Символически это записывается так:
a2 + b2 = c2.
Задача 154. На одной прямой на равном расстоянии друг от друга стоят три телеграфных столба. Крайние находятся от дороги на расстояниях 18 м и 48 м. Найдите расстояние, на котором находится от дороги средний столб.
Ответ: 33.
Задача 155. На одной прямой на равном расстоянии друг от друга стоят три телеграфных столба. Первый и второй находятся от дороги на расстояниях 15 м и 20 м. Найдите расстояние, на котором находится от дороги третий столб.
Ответ: 25.
Задача 156. Мальчик прошел от дома по направлению на восток 800 м. Затем повернул на север и прошел 600 м. На каком расстоянии от дома оказался мальчик?
Ответ: 1000 м.
Задача 157. Девочка прошла от дома по направлению на запад 500 м. Затем повернула на север и прошла 300 м. После этого она повернула на восток и прошла еще 100 м. На каком расстоянии от дома оказалась девочка?
Ответ: 500 м.
Задача 158. Мальчик и девочка, расставшись на перекрестке, пошли по взаимно перпендикулярным дорогам, мальчик со скоростью 4 км/ч, девочка – 3 км/ч. Какое расстояние (в км) будет между ними через 30 мин?
Ответ: 2,5.
Задача 159. Два парохода вышли из порта, следуя один на север, другой на запад. Скорости их равны соответственно 15 км/ч и 20 км/ч. Какое расстояние будет между ними через 2 ч?
Ответ: 50 км.
Задача 160. Используя данные, приведенные на рисунке, найдите расстояние в метрах между пунктами A и B, расположенными на разных берегах озера.
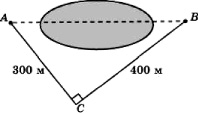
Ответ: 500 м.
Задача 161. Лестница длиной 12,5 м приставлена к стене так, что расстояние от ее нижнего конца до стены равно 3,5 м. На какой высоте от земли находится верхний конец лестницы?
Ответ: 12 м.
Задача 162. На какое расстояние следует отодвинуть от стены дома нижний конец лестницы, длина которой 13 м, чтобы верхний ее конец оказался на высоте 12 м?
Ответ: 5 м.
Задача 163. Какой длины должна быть лестница, чтобы она достала до окна дома на высоте 8 метров, если ее нижний конец отстоит от дома на 6 м?
Ответ: 10 м.
Задача 164. В 60 м одна от другой растут две сосны. Высота одной 31 м, а другой – 6 м. Найдите расстояние между их верхушками.
Ответ: 65 м.
Задача 165. Стебель камыша выступает из воды озера на 1 м. Его верхний конец отклонили от вертикального положения на 2 м, и он оказался на уровне воды. Найдите глубину озера в месте, где растет камыш.
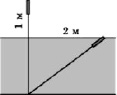
Ответ: 1,5 м.
Задача 166. Из круглого бревна нужно вырезать брус с поперечным сечением 5×12 (см). Какой наименьший диаметр должно иметь бревно?
Ответ: 13 см.
Задача 167. Отношение высоты к ширине экрана телевизора равно 0,75. Диагональ равна 60 см. Найдите ширину экрана.
Ответ: 48 см.
Задача 168. Какого наименьшего диаметра должен быть цилиндрический сосуд, чтобы в него можно было поместить деталь в форме прямоугольного параллелепипеда с размерами 6×8×10 (см)?
Ответ: 10 см.
Задача 169. Туннель в сечении имеет форму полукруга радиуса 3 м. Какой наибольшей высоты должна быть машина шириной 2 м, чтобы она могла проехать по этому туннелю?
В ответе укажите приближенное значение в метрах с точностью до одного знака после запятой.
Ответ: 2,8 м.
Задача 170. Какое наименьшее ребро должна иметь кубическая коробка, чтобы в нее поместился тетраэдр с ребром, равным 8 см? В ответе укажите целое число сантиметров.
Ответ: 6 см.
Задача 171. В одном углу кубической коробки с размерами 40×40×40 (см) сидит муха. В противоположном углу сидит паук. Найдите длину кратчайшего пути по поверхности коробки, по которому паук может доползти до мухи. В ответе укажите приближенное значение, равное целому числу сантиметров.
Задача 172. В одном углу комнаты с размерами 4×5×3 (м), сидит муха. В противоположном углу сидит паук. Найдите длину кратчайшего пути по поверхности комнаты, по которому паук может доползти до мухи. В ответе укажите приближенное значение в метрах с точностью до одного знака после запятой.
Задача 173. На вершинах двух елок сидят две вороны. Высота елок равна 4 м и 6 м. Расстояние между ними равно 10 м. На каком расстоянии BE нужно положить сыр для этих ворон, чтобы они находились в равных условиях, т.е. чтобы расстояния от них до сыра было одинаковыми?
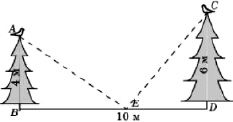
Задача 174. В 800 м от места взлета самолета расположены деревья высотой до 20 м. Под каким углом должен подниматься самолет, чтобы не задеть деревья.
Ответ: не менее 1°5′.
