Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

ЭНЕРГОЭФФЕКТИВНЫЕ СИСТЕМЫ ГИДРАВЛИЧЕСКИХ ПРИВОДОВ ШАГАЮЩИХ МАШИН: МОНОГРАФИЯ

Семенов С. Е., Щербачев П. В., Тарасов О. И.,

Особенности математического моделирования шагающих машин

При проектировании шагающих машин, стоит обратить особое внимание на математическое моделирование как исполнительных приводов, так и всей системы в целом. Шагающие машины, по кинематической структуре следует рассматривать как механизмы с ветвящейся кинематической структурой. Математический аппарат, предназначенный для работы с механизмами в виде неветвящихся кинематических цепей, развивался прежде всего в робототехнике. Это объясняется быстрым прогрессом промышленной робототехники, где в подавляющем большинстве случаев ИМ представляют собой простые (не ветвящиеся) кинематические цепи, закрепленные одним концом к неподвижному основанию. Однако теория механизмов со структурой ветвящихся кинематических цепей (кинематических деревьев) развита
недостаточно.

Для математического описания ИМ с линейной кинематической структурой (в виде простой кинематической цепи) чаще всего пользуются математическим аппаратом, использующим специальные системы координат Денавита-Хартеберга и рекурсивные алгоритмы [2, 6]. Каждое звено обозначают номером, соответствующим его порядковому номеру в цепи, начиная от основания. Однако многие механизмы содержат несколько простых кинематических цепей. Это, например, мобильные машины с двумя и более манипуляторами, шагающие машины. При этом утрачивает смысл простой порядковый номер, а структура рекурсивных алгоритмов становится значительно более сложной.

В процессе движения звенья ИМ контактируют с подвижными и неподвижными окружающими телами, а также между собой. Говоря иначе, на звенья накладываются дополнительные голономные и неголономные связи, и возникают замкнутые кинематические цепи. Для учета этих связей в систему уравнений, описывающих поведение ИМ, должны быть добавлены соответствующие уравнения. При помощи дополнительных уравнений связей кинематическим деревом, а в некоторых случаях и простой цепью, могут быть описаны и механизмы с изначально замкнутой структурой.

Известны методы математического описания структуры древовидных механизмов, использующие теорию графов. Например, в [17] структура взаимосвязей звеньев древовидного механизма отображается графом системы. Вершины представляют звенья механизма, а ребра – шарниры. Для обеспечения возможности различать звенья использован ориентированный граф. Его структура задается при помощи матрицы инцидентности. Для каждого звена записываются уравнения его движения как твердого тела. Дополнительно записываются уравнения, соответствующие как постоянным связям, формирующим структуру механизма, так и переменным, возникающим и исчезающим в процессе движения. Размерность системы уравнений получается очень большой. В робототехнике разработаны методы, позволяющие записывать уравнения движения ИМ с линейной структурой сразу с учетом его внутренних связей, формирующих его кинематическую структуру [18, 22]. Если не наложено дополнительных внешних связей, то система уравнений динамики механизма имеет размерность, равную числу его степеней подвижности. При наложении дополнительных связей добавляется соответствующее количество уравнений, однако система остается значительно более компактной и удобной в использовании.

Авторами работ в научных статьях [20, 21] предложена усовершенствованная методика, позволяющая благодаря использованию элементов теории графов и специальной системы нумерации звеньев формировать компактную математическую модель и для древовидных ИМ (рис. 1).

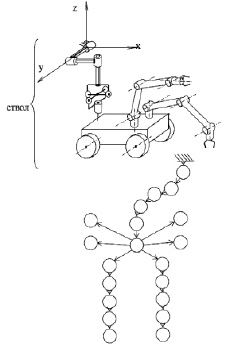
Рис. 1. Древовидный исполнительный механизм и соответствующий граф

Как и в [17], вершины в этом графе представляют звенья механизма, а ребра – соединяющие их кинематические пары пятого класса. Если звенья механизма соединены парой более низкого класса (k < 5), то при составлении графа между соответствующими им вершинами вводятся 5 – k дополнительных вершин, которые реальные звенья не представляют. Они соединяются парами 5-го класса таким способом, чтобы вместе имитировать исходный реальный шарнир. Добавляемые звенья можно представить себе, как фиктивные (воображаемые) звенья с нулевой массой. Корнем дерева будем считать какое-либо тело (реальное или воображаемое), фиксированное в абсолютной системе координат, т.е. системе, относительно которой рассматривается движение механизма. В случае если исполнительный механизм не закреплен к неподвижному основанию (стойке), представим, что он связан со стойкой кинематической парой нулевого класса и введем фиктивную кинематическую цепь из пяти вершин (ствол дерева), привязывающую какое-либо звено реального механизма к условной неподвижной стойке. Ствол можно представить, как пять невесомых звеньев, соединенных между собой, со стойкой и ИМ тремя поступательными и тремя вращательными кинематическими парами пятого класса. Соответствующие шарнирные силы и моменты заведомо равны нулю.

Таким образом, наличие ствола не оказывает влияния на движение ИМ, но позволяет «привязать» движение ИМ к абсолютной системе координат с использованием лишь традиционных для робототехники методов.

Звенья (а также соответствующие им вершины графа) и степени подвижности механизма необходимо каким-либо образом обозначить. Звенья, непосредственно следующие за ветвящимся звеном (или, в терминах теории графов, его звенья-сыновья), могут быть пронумерованы по-разному. Поэтому понятие порядкового номера звена для древовидного механизма не имеет смысла. В принципе, звенья такого механизма можно обозначить произвольно, однако для удобства и наглядности примем следующий способ:

– стойке (реальной или условной) присвоим номер 0;

– если робот не закреплен к неподвижному основанию, звенья ствола (фиктивной кинематической цепи) пронумеруем от стойки последовательно от 1 до 5;

– первые три степени ствола – поступательные, остальные вращательные;

– реальные звенья простых кинематических цепей, составляющих дерево, нумеруются без пропусков в возрастающем порядке
от корня; при этом получается, что собственный номер звена всегда меньше номера любого звена-потомка;

– номера сочленений такие же, как и у звеньев, присоединяемых этими сочленениями к предыдущему звену (в терминах теории графов – звену отцу).

Для работы с ИМ как с деревом будем использовать, в частности, следующие принятые в теории графов функции и термины:

dg+(i) – полустепень исхода звена (вершины) с номером i, определяющая количество звеньев-сыновей звена i;

d(i, j) – длина пути из вершины i в вершину j, равняющаяся количеству ребер на пути;

Dnum(i) – определяет глубинный номер звена i (т.е. его порядковый номер при поиске в глубину от корня дерева).

Также используем следующие обозначения:

Dnumk(i) – глубинный номер звена i при поиске в глубину
от звена k;

D – матрица достижимости. Если звено i достижимо из звена j, т.е. имеется ориентированный путь из вершины j в вершину i, dij = 1, иначе dij = 0. Звено i достижимо из самого себя. Такая матрица достижимости является транспонированной по отношению к матрице достижимости C, принятой в теории графов.

L = {1, 2, …, N} – неупорядоченное множество, элементами которого являются номера звеньев ИМ;

N – полное количество звеньев, включая фиктивные, исполнительного механизма (количество вершин графа);

Г(i) – кортеж номеров звеньев, являющихся для звена i следующими (звеньями-сыновьями); кортеж содержит dg+(i) элементов.

σi ∈ {0, 1} – множитель, определяющий тип сочленения звена i со звеном-отцом;

σi = 1 – сочленение вращательное;

σi = 0 – сочленение поступательное.

Для удобства обозначения физических величин и индексации переменных введем следующие функции:

s(i, k) – определяет номер звена, являющегося kм следующим звеном (k-й вершиной-сыном) для звена i;

f(i) – номер звена, являющегося предыдущим (вершиной-от-
цом) для звена i;

ns(i) – определяет, каким по счету следующим из числа непосредственно присоединенных является звено i для своего предыдущего звена;

p(i, j, k) – определяет номер k-й вершины пути из i в j.

Эти функции вычисляются с использованием разработанных в теории графов алгоритмов и далее используются для определения порядка обхода (перебора вершин) дерева при организации вычислений, а также в качестве индексов при обозначении физических величин, относящихся к конкретным звеньям.

Для записи уравнений механики исполнительных механизмов в робототехнике принято с каждым звеном связывать свою систему координат, и чаще всего это системы координат Денавита – Хартенберга (ДХ) [18,20, 21, 22]. Однако при описании древовидных механизмов из-за использования ДХ-систем приходится с ветвящимся звеном связывать столько систем координат, сколько следующих звеньев оно имеет. Приходится вводить и дополнительные матрицы преобразования, связывающие эти системы между собой. В данной работе предлагается более удобный метод. Используем связанные со звеньями системы координат, оси O-zi которых проходят через ось сочленения звена i со звеном f(i) (предыдущим звеном), а не следующим, как в случае использования ДХ-систем. В общем случае для перехода из системы i в систему f(i) требуется 6 элементарных преобразований (три вдоль и три вокруг осей), однако в большинстве случаев можно назначить системы пользуясь специальными правилами и, как и при использовании ДХ-систем, обойтись четырьмя элементарными движениями. Эти правила следующие:

1) ось zi совпадает с осью сочленения i-го и предыдущего звеньев;

2) ось xf(i) предыдущего звена пересекает под прямым углом ось zi.

Тогда матрица перехода Ai соответствует четырем последовательным элементарным движениям:

1. Поворот системы f(i) на угол αi вокруг оси xf(i) до совпадения направлений осей zf(i) и zi.

2. Перенос системы f(i) на расстояние ai вдоль оси xf(i) до совпадения осей zf(i) и zi.

3. Перенос системы f(i) на расстояние di вдоль оси zf(i) до совпадения начал координат систем i и f(i).

4. Поворот системы f(i) на угол θi вокруг оси zf(i) до совпадения всех осей.

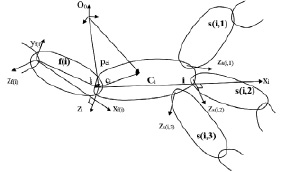
Рис. 2. Специальные системы координат для древовидных механизмов

Сумме этих движений соответствует матрица вида

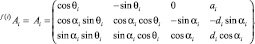
Однако, если у звена есть несколько следующих звеньев, то в общем случае не для всех них второй пункт приведенных правил выполним. Тогда соответствующие матрицы А нужно формировать при помощи шести элементарных движений, предварив вышеперечисленные четыре следующими двумя:

1. Поворот системы f(i) на угол βi вокрг ее оси Yf(i) до тех пор, пока оси Xf(i) и Zi не станут скрещиваться под прямым углом.

2. Перенос системы f(i) на bi вдоль оси Yf(i) до пересечения осей Xf(i) и Zi под прямым углом.

Этим движениям соответствует матрица преобразования

Матрица преобразования Аi в этом случае имеет вид:

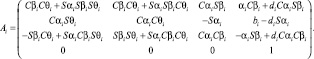
На практике целесообразно при назначении связанных систем координат для всех звеньев пытаться выполнить оба приведенных выше правила. Если удается обеспечить пересечение осей xf(i) предыдущего звена и оси zi под прямым углом, то параметры bi и βi заведомо становятся равными нулю. Для упрощения вычислительных алгоритмов матрицы Ai следует вычислять по последней формуле. При движении механизма изменяется лишь один параметр – либо θi для вращательных пар, либо di для поступательных, поэтому вычислять матрицы Ai можно в два приема. На этапе инициализации следует вычислить величины, входящие в Аi, но не зависящие от θi либо di (в зависимости от вида сочленения), а в процессе управления ИМ или при его моделировании вычислять ее текущее значение с использованием сделанной заготовки. Таким образом, наличие в формулах βi и bi практически не увеличивает трудоемкости вычислений.

В качестве обобщенных координат ИМ многих видов машин, в частности роботов, принято выбирать углы во вращательных и перемещения в поступательных сочленениях. Номер обобщенной координаты, как и номер соответствующего сочленения, такой же, как и у звена, присоединяемого этим сочленением к предыдущему звену.

Компактность и наглядность записи уравнений существенно зависит от способа индексации. В литературе по робототехнике используют до трех индексов у любой переменной. Правый нижний указывает номер звена, к которому относится данная величина, левый верхний – номер системы координат, в которой она представлена, а правый верхний – специальный символ (например, знак транспонирования или возведения в степень). Традиционно для простых кинематических цепей при необходимости сослаться на предыдущее или последующее звенья по отношению к звену i пишут, например, Ti + 1 или Ti–1. В случае древовидного ИМ такая запись теряет смысл, т.к. у звена может быть несколько следующих звеньев, поэтому при описании древовидного механизма для обозначения какой-либо величины x, относящейся к предыдущему или следующему звену для звена i, используем записи xf(i) и xs(i,j) соответственно. Здесь j – порядковый номер следующего звена в списке непосредственно присоединенных к звену i следующих звеньев; j ∈ Γ(i).

Векторные и тензорные величины могут задаваться в различных СК. В какой именно СК задана данная величина, указывает его левый верхний индекс. Если этот индекс отсутствует или нулевой, то величина задана в базовой (абсолютной) СК; если указано некоторое целое отличное от нуля число i, то вектор задан в СК звена i. Если в качестве индекса стоит с, то он задан в системе того звена, к которому сам и относится.

С каждым звеном i свяжем 4×4 матрицу Ai перехода к системе координат предыдущего звена и 4×4 матрицу Ti перехода к абсолютной системе [2, 6]. В блочном виде

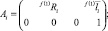
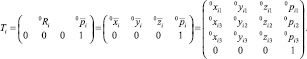
В последнем выражении x, y и z – направляющие векторы осей системы координат звена i, а p – радиус-вектор начала системы координат звена i. Эти векторы выражены в абсолютной системе координат.

Если звенья абсолютно жесткие, в связанных со звеньями системах координат

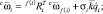
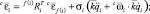
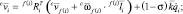
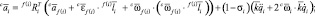
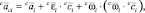
где  –	угловая скорость звена i;
–	угловое ускорение звена i;
–	скорость начала системы координат звена i;
–	i-я обобщенная скорость, равная скорости взаимного перемещения звеньев i и предыдущего ему звена f(i);
–	i-е обобщенное ускорение;
–	вектор, соединяющий начало СК предыдущего для i звена, с началом СК звена i;
–	вектор положения центра масс звена i;
–	ускорение начала системы координат звена i;
–	ускорение центра масс звена i.

В этих выражениях звено с номером 0 (стойка) считается неподвижным. Индекс i принимает значения, соответствующие последовательному нарастанию их глубинных номеров при поиске в глубину от корня.

i = Dnum–1(n); n = 1, …, N.

Такой порядок соответствует прямой рекурсии для простых кинематических цепей. Мы также называем его прямой рекурсией.

Важным средством решения кинематических задач является матрица Якоби, позволяющая связать угловую скорость какого-либо звена механизма и линейную скорость какой-либо его точки с обобщенными скоростями ИМ.

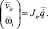
Для вычисления матрицы Якоби, соответствующей звену i и его точке r, обозначим ее столбцы как jk, где k – номер столбца.

Jir = (j1 ... jk ... jN).

Тогда, если на механизм не наложены дополнительные внешние связи, столбцы могут быть вычислены следующим образом:

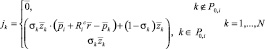
Проверка, лежит ли вершина k на пути из корня к вершине i может быть сделана по матрице достижимости. Если dik = 1, то k ∈ P0,i иначе, нет.

После того, как по известным обобщенным координатам, скоростям и ускорениям вычислены угловые скорости и ускорения звеньев механизма, а также линейные ускорения центров масс звеньев, в порядке обратной рекурсии вычисляются силы и моменты, приложенные к звеньям, а также нагрузки на приводы (шарнирные моменты и силы).

В связанных системах координат сила и момент, действующие со стороны звена i на предыдущее звено, вычисляются следующим образом:

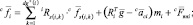
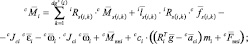
где Fвн –	внешние силы, действующие на звено i;
Mвн –	моменты внешних сил, действующих на звено i относительно его центра тяжести.

Шарнирные моменты (силы)

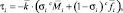
где k = (0,0,1)T.

Именно такие шарнирные силы и моменты должны развивать привода, чтобы реализовать принятые в прямой рекурсии ускорения.

Эти вычисления производятся в обратном порядке перечисления глубинных номеров

i = Dnum–1(n), n = N, ..., 1.

Уравнения динамики ИМ в случае, если на них не наложены дополнительные связи, могут быть записаны в следующей форме [18, 22]

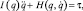
где I –	матрица инерции;
Н –	матрица-столбец приведенных к степеням подвижности центробежных и кориолисовых сил, а также внешних нагрузок;
τ –	вектор шарнирных сил и моментов.

Такая форма записи дает возможность по известным шарнирным силам и моментам вычислить обобщенные ускорения. Обобщенные ускорения, в свою очередь, могут быть использованы для моделирования движения ИМ, а также для управления ИМ. Однако для этого необходимо предварительно вычислить матрицы I(q) и .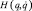

Матрица инерции – это квадратная положительно определенная симметричная матрица, характеризующая инерционные свойства механизма. Она зависит от геометрии, масс, тензоров инерции звеньев механизма, а также от его текущей конфигурации, т.е. от текущих значений обобщенных координат. Она не зависит от обобщенных скоростей, ускорений, наложенных внешних связей. Столбцы матрицы инерции вычислим как векторы шарнирных моментов (сил), вызывающих единичные ускорения по соответствующим этим столбцам обобщенным координатам. Для расчета i-го столбца положим при текущих значения обобщенных координат i-е обобщенное ускорение равным 1, а остальные – равными 0. Обобщенные скорости также примем равными 0. Далее при текущих значениях обобщенных координат используя приведенные выше кинематические соотношения в порядке прямой рекурсии рассчитаем угловые и линейные ускорения для звеньев

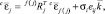
где eij –

элемент c номерами ij единичной матрицы Е (равен 1 если i = j, иначе 0)

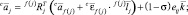
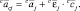
Порядок перебора индексов:

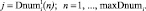
Невычисленным ускорениям присваиваются нулевые значения.

В обратной рекурсии производятся вычисления сил и моментов, действующих на звенья, а также шарнирных моментов (сил).

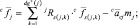
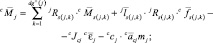
Тогда элементы матрицы инерции

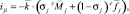
Порядок перебора индексов:

j = Dnum–1(n), n = N, ..., 1.

Столбцы матрицы инерции могут вычисляться по порядку:

i = 1, ..., N.

Вычисления элементов матрицы инерции можно оптимизировать, учитывая ее симметричность.

Для расчета элементов матрицы-столбца H центробежных, кориолисовых и внешних сил в прямой рекурсии необходимо найти угловые и линейные ускорения звеньев при равных нулю обобщенных ускорениях.

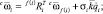
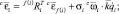
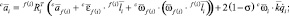
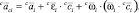
Порядок перечисления индексов

i = Dnum–1(n); n = 1, …, N.

В порядке обратной рекурсии вычисляются силы и моменты, приложенные к звеньям, а также шарнирные моменты (силы), которые и равны элементам матрицы H.

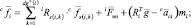
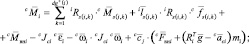
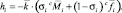
Порядок перечисления индексов

i = Dnum–1(n); n = 1, …, N.

Если ИМ не закреплен к неподвижному основанию, то первые шесть степеней подвижности, как условились ранее, относятся к фиктивной кинематической цепи. Матричное уравнение динамики перепишем в блочно-матричном виде, обозначив индексом I подматрицы, относящиеся к фиктивной кинематической цепи, а индексом R – к реальным звеньям механизма.

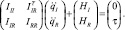
Здесь III – 6×6 часть матрицы инерции, соответствующая фиктивной кинематической цепи (стволу дерева); IIR – (N – 6)×6 часть матрицы инерции, определяющая взаимовлияние фиктивных и реальных степеней подвижности механизма; IRR – (N – 6)∙(N – 6) часть матрицы инерции, соответствующая реальной части дерева; и  – части вектора обобщенных ускорений механизма, соответствующие фиктивной кинематической цепи и реальному механизму; HI и HR – части матрицы-столбца приведенных центробежных, кориолисовых, весовых и внешних сил, действующих на звенья механизма; τ – вектор шарнирных сил и моментов.

Наличие нулевого вектора в верхней части матрицы шарнирных моментов объясняется тем, что фиктивная кинематическая цепь не оказывает никакого сопротивления движению.

Звенья ИМ могут контактировать с окружающими предметами и между собой. В математической модели это учитывается введением дополнительных уравнений связей, причем в процессе движения они могут изменяться, может меняться их количество. Связи могут устанавливаться с подвижными предметами, в частности, с другими ИМ. Уравнения как голономных, так и неголономных связей, выраженные относительно обобщенных ускорений, можно записать в следующем виде:

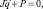
где J –	матрица Якоби размерностью M×N;
M –	количество связей;
P –	матрица столбец размерностью M.

Если ИМ не закреплен к неподвижному основанию, и первые шесть обобщенных координат соответствуют фиктивной кинематической цепи, это выражение можно представить в блочно-матричном виде:

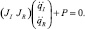
Если на механизм наложены связи, то возникают реакции связей R – силы, действующие со стороны препятствий на механизм так, что заставляют его двигаться в соответствии с уравнениями связей. Они, также как и другие силы, вносят свой вклад в шарнирные моменты и силы.

τR = –JTR.

Тогда уравнения динамики незакрепленного к неподвижному основанию механизма с учетом связей запишутся следующим образом:

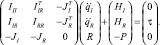
Общие выражения для вычисления J и P достаточно громоздки, а соответствующие вычисления трудоемки. Поэтому для работы в реальном времени и моделирования целесообразно использовать более простые выражения, полученные для конкретных видов связей. Для примера рассмотрим уравнения связей, ограничивающих подвижность некоторой точки звена i. Пусть, например, зафиксирована некоторая точка r звена i (обозначим ее ri). Соответственно, скорость и ускорение этой точки равны 0. Для скорости справедливо выражение

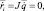
а для линейного ускорения

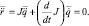
Первое слагаемое – это составляющая воображаемого ускорения рассматриваемой точки, вызванная обобщенными ускорениями. Второе слагаемое (вектор P) – составляющая, вызванная обобщенными скоростями.

Пользуясь линейностью последнего выражения относительно обобщенных ускорений, положим обобщенные ускорения равными нулю и вычислим ускорение точки ri. В связанных системах координат

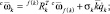
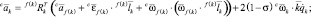
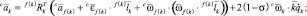
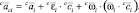
порядок вычислений

k = p(0, i, l), l = 2, ..., d(0, i).

Ускорение точки ri

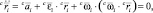
Матрица P в этом случае вычисляется как вторая производная вектора ri положения точки наложения связи, выраженная в абсолютной системе:

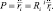
Данный способ особенно удобен тем, что при моделировании вычисления по большинству из приведенных выше формул необходимы также для вычисления матрицы H уравнения динамики.

Алгоритм вычисления матрицы Якоби, входящей в уравнения связей, может быть построен следующим образом:

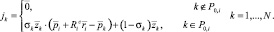
где jk – k-й столбец матрицы Якоби.

Внешние силы, действующие на исполнительный механизм ДШР в процессе движения, могут быть ударными и неударными. Ударные силы отличаются от неударных тем, что время их действия мало, а величина может быть очень большой, поэтому результат их действия на движение механизма может быть значительным. Однако малое время их действия позволяет считать, что конфигурация механизма, а следовательно, и матрица инерции I, существенно измениться не успевают. Центробежные и кориолисовы силы, действующие на звенья механизма, не могут носить ударный характер. Примем, что внешние силы, учитываемые матрицей H, также не ударные. Тогда ударными остаются только реакции связей, и на время действия удара всеми силами, в том числе и развиваемыми приводами, можно пренебречь (справедливость последнего предположения зависит от типа используемых приводов; оно справедливо, например, при использовании гидравлических приводов). В результате уравнения динамики примут следующий вид:

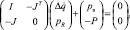
где  –	изменение обобщенных скоростей за время удара;
pв –	приведенный ударный импульс внешних сил;
pR –	ударный импульс реакций связей.

В процессе движения внешние связи, наложенные на ИМ, могут изменяться. Причем в некоторых случаях при мгновенном изменении связей, как, например, в случае встречи с препятствием, этот процесс будет сопровождаться ударом и практически мгновенным изменением скоростей механизма. Пусть исходное уравнение связей имеет вид:

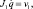
а после изменения

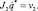
Тогда за время изменения связей имеем:

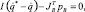
где JB – матрица Якоби ударных сил.

В момент изменения связей старые связи исчезают, и исчезают вызванные ими реакции R1. Они не имели порядок ударных сил, поэтому и их исчезновение не носит ударный характер. В этот же момент накладываются новые связи, и соответствующие им реакции R2 приводят к мгновенному изменению скоростей, поэтому они носят ударный характер. Отсюда следует, что

JB = J2.

В результате получаем выражение для вычисления скоростей после мгновенного изменения связей:

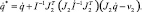
Представленные уравнения и алгоритмы позволяют моделировать движение множества различных машин, исполнительные механизмы которых могут быть представлены как кинематические деревья. Также данные уравнения позволяют строить различные алгоритмы управления механизмами. На кафедре Э-10 МГТУ им. Н.Э. Баумана совместно с МИПК создан лабораторный двуногий шагающий робот с электрогидравлическим следящим приводом, способный перемещаться в рамках динамической ходьбы. Приведенные подходы к формированию математической модели, соответствующие уравнения и алгоритмы использованы для управления его исполнительной системой, а также для синтеза законов управления движением. Видео можно найти в интернете по адресу http://www.youtube.com/watch?v = Ld0E5qt46uA.