
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания

ЭНЕРГОЭФФЕКТИВНЫЕ СИСТЕМЫ ГИДРАВЛИЧЕСКИХ ПРИВОДОВ ШАГАЮЩИХ МАШИН: МОНОГРАФИЯ
Семенов С. Е., Щербачев П. В., Тарасов О. И.,
ЭЛЕКТРОГИДРАВЛИЧЕСКИЕ ПРИВОДЫ С ДРОССЕЛЬНЫМ РЕГУЛИРОВАНИЕМ
Электрогидравлические приводы с дроссельным регулированием широко применяются в различных областях техники для получения вращательных и поступательных движений звеньев механизмов. Исполнительным двигателем в таком приводе может быть гидроцилиндр или гидромотор. Управление ими осуществляется при помощи сервораспределителей или распределителей с пропорциональным управлением. Дроссельное регулирование дает широкие возможности для реализации различных законов управления, создания следящих систем, замкнутых обратной связью по координате (углу поворота или перемещению) или скорости (линейной или угловой).
При всех достоинствах, дроссельное регулирование обладает весьма существенным недостатком. Дросселирование жидкости на щелях распределяющих устройств приводит к существенным потерям мощности. В отличие от привода с объемным регулированием, где давление в гидросистеме главным образом зависит от величины нагрузки на привод, при использовании дроссельного управления для стабильной работы привода необходимо поддерживать постоянный высокий уровень давления питания. Обычно этого добиваются, применяя насосы с регулятором давления и устанавливая с систему гидроаккумулятор. Превышение давления питания над величиной, необходимой для движения нагрузки, создает большой запас по усилию на выходном звене привода. На некоторых режимах этим «запасом» можно воспользоваться и, применив специальные алгоритмы управления, повысить энергоэффективность дроссельного привода.
Приводы, установленные в СП ИМ мобильных роботов, образуют единую многосвязную систему. Они испытывают существенное взаимовлияние через ИМ и общий источник энергии ограниченной
мощности, поэтому управлять приводами целесообразно при помощи многомерного регулятора. Однако известное «проклятие размерности» делает синтез регуляторов для таких систем чрезвычайно сложным и трудоемким. Задача осложняется и тем, что в процессе движения конфигурация ИМ постоянно меняется. Меняются внешние нагрузки, возникают и исчезают внешние механические связи, соответственно изменяются и массо-инерционные характеристики ИМ. Это требует постоянного изменения настроек регулятора в реальном времени, причем в условиях неполной и зашумленной информации о текущем состоянии и параметрах объекта управления. Подобная задача адаптации для столь сложных многомерных систем на практике по-прежнему является трудноразрешимой.
Альтернативным является подход, предполагающий создание упрощенных систем управления, обладающих определенной робастностью. Робастностью обычно называют способность системы функционировать в условиях неопределенности, устойчивость к нарушению исходных предпосылок или просто ошибкоустойчивость. По-прежнему остается популярным метод синтеза систем управления приводами, при котором приводы первоначально считаются действующими независимо и рассчитываются исходя из наихудшего сочетания приведенных масс (моментов инерции) и статических нагрузок. Далее производится коррекция полученного решения по результатам моделирования, учитывающего взаимовлияние приводов, внешние связи и другие особенности функционирования. Система в этом случае не является оптимальной, но во многих случаях позволяет решать поставленные практические задачи.
Типичными представителями машин со сложными ИМ являются роботы и манипуляторы. На многих из них, и, как правило, на роботах очень большой грузоподъемности и экстремальных роботах, используют гидравлические и электрогидравлические приводы. Например, гидроприводы используют на подводных манипуляторах, под землей, в условиях повышенной влажности
и запыленности, на кранах-манипуляторах, экскаваторах, а также на различных шагающих машинах. К преимуществам гидроприводов можно отнести большую удельную мощность, высокое быстродействие, хорошую компонуемость в различные машины и агрегаты, высокие надежность и ресурс, стойкость к неблагоприятным факторам внешней среды: влаге, пыли, высокому и низкому внешнему давлению, высоким и низким температурам, ударам, вибрациям и т.д. Однако они дороги, сложны в эксплуатации, а также обладают некоторыми динамическими особенностями, требующими специальных подходов при управлении системами гидроприводов.
Структурная схема, соответствующая линеаризованным уравнения математической модели типичного одноканального дроссельного электрогидравлического привода с симметричным гидроцилиндром приведена на рис. 42. Современные электрогидравлические усилители (ЭГУ) имеют высокое быстродействие, благодаря чему в большинстве случаев определяющее влияние на динамику приводов оказывают исполнительные гидродвигатели (ГД) совместно с присоединенными к выходному звену механизмами. Демпфирование при этом определяется коэффициентами kQp и b. Причем kQp пропорционален смещению золотника xз, поэтому при позиционировании привода демпфирование уменьшается, и в случае малости утечек через закрытые золотниковые щели определяется в основном трением в уплотнениях (ГД). Однако параметры трения в уплотнениях не стабильны и зависят от множества факторов, изменяющихся в процессе эксплуатации привода: перепада давления на уплотнениях, температуры рабочей жидкости, состояния рабочих поверхностей, степени старения материалов уплотнений.
Также при работе манипуляционной системы изменяется масса, приведенная к штоку ГД, нагрузка на привод. Соответственно изменяются параметры передаточной функции, описывающей привод, вид его ЛАХ и ЛФХ. В результате образуется некоторая область вероятного расположения вершины резонансного пика привода на плоскости ЛАХ (рис. 43).
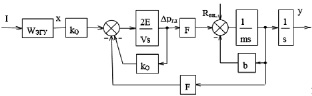
Рис. 42. Структурная схема разомкнутого электрогидравлического привода, где I – ток управления; xз – смещение золотника; Δpгд – разница давлений в полостях ГД; Rвн – внешняя нагрузка; yш – перемещение штока ГД; WЭГУ – передаточная функция электрогидравлического усилителя; kQx; kQp – коэффициенты линеаризации расходно-перепадной характеристики золотника; E – объемный модуль упругости жидкости;
V – объем полостей ГД; F – площадь поршня ГД;
m – приведенная к штоку ГД масса; b – коэффициент вязкого трения

Рис. 43. ЛАХ силовой части гидропривода
Вероятность появления высоких пиков в низкочастотной области вынуждает для получения необходимых запасов по фазе и амплитуде либо снижать добротность по скорости, либо искать способы динамической коррекции. Введение демпфирующих обратных связей по скорости для гидроприводов оказывается малоэффективным из-за невозможности введения глубоких обратных связей. В авиации, например, с подобной проблемой столкнулись при проектировании приводов рулей тяжелых самолетов. Там стали использовать гидромеханическую коррекцию по динамическому давлению [47]. Подобного эффекта можно добиться и при помощи электрической обратной
связи по относительному ускорению выходного звена привода. Однако это ускорение трудно измерить, поэтому на практике, как правило, используют сигналы с датчиков давления, установленных в полостях ГД, т.к в одностепенной системе ускорение выходного звена пропорционально перепаду давления с точностью до влияния внешних нагрузок. Для уменьшения влияния этих нагрузок и повышения жесткости привода в обратной связи по перепаду давления устанавливают устройство, описываемое интегродифференцирующим звеном с передаточной функцией
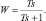
Его постоянную времени выбирают так, чтобы оно не пропускало постоянную составляющую сигнала обратной связи и уменьшало влияние низкочастотных колебаний, связанных с внешней нагрузкой, но оставляло без изменения сигнал в среднечастотной области, определяющей устойчивость и динамические свойства привода. На рис. 44 приведена соответствующая структурная схема, на которой ka/m – коэффициент обратной связи по динамическому давлению.
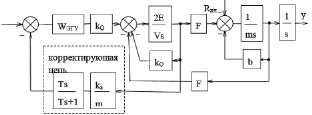
Рис. 44. Структурная схема разомкнутого привода с обратной связью
по динамическому давлению
Пользуясь методом обратных характеристик [49], можно показать, что в результате ЛАХ привода будет лежать не выше линии АС (рис. 45), которая является отражением относительно горизонтальной оси ЛАХ корректирующей цепи. Таким образом, резонансный пик вне зависимости от места своего расположения будет «срезан».

Рис. 45. Коррекция частотных характеристик разомкнутого привода
при помощи обратной связи по динамическому давлению
Однако данный метод непосредственно не применим для многостепенных систем с сильным взаимовлиянием приводов через исполнительный механизм, к которым относятся роботы. Для них связь ускорений в степенях подвижности, внешних нагрузок, шарнирных сил и моментов, развиваемых приводами и массо-инерционных характеристик исполнительного механизма с учетом внешних связей и текущей конфигурации описывается блочно-матричным уравнением [48, 8]
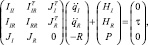
|
где III, IIR, IRR – |
компоненты блочной матрицы инерции; |
|
JI, JR – |
компоненты блочной матрицы Якоби уравнений внешних связей, наложенных на механизм; |
|
HI, HR – |
компоненты матрицы столбца приведенных к степеням подвижности центробежных, кориолисовых и внешних сил; |
|
P – |
матрица-столбец уравнений связей, зависящая от скоростей; |
|
qI, qR – |
компоненты вектора обобщенных координат исполнительного механизма; |
|
R – |
вектор реакций связей; |
|
τ – |
вектор шарнирных моментов и сил, развиваемых приводами. |
На кафедре Э-10 МГТУ им. Н.Э. Баумана создан двуногий шагающий робот (ДШР), имеющий 12 управляемых степеней подвижности, оснащенных электрогидравлическими следящими приводами. Автор использовал данное блочно-матричное уравнение для определения относительных ускорений в приводах ДШР по измеренным давлениям в полостях гидродвигателей и нагрузкам на стопах робота с целью коррекции с их помощью динамических свойств системы приводов.
При малых скоростях движения (когда гидропривод оказывается наименее демпфирован) можно пренебречь центробежными и кориолисовыми силами, а также внешними силами с их преимущественно низкочастотным спектром. Тогда получим упрощенную систему уравнений
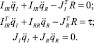
Преобразуя данную систему, получим матричное выражение для вычисления обобщенных ускорений, определяющих относительные ускорения в приводах
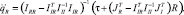
Эти ускорения (произведя предварительно описанное выше интегродифференцирующее преобразование) можно использовать для демпфирования приводов. Данный метод позволил повысить добротность приводов ДШР по скорости в 3…10 раз и обеспечить динамическую точность приводов до уровня, позволившего реализовать динамическую ходьбу робота (http://www.youtube.com/watch?v = Ld0E5qt46uA). На рис. 46 показаны экспериментальные кривые, иллюстрирующие влияние глубины демпфирующих обратных связей по динамическому давлению на качество работы приводов. В ходе эксперимента робот стоял на правой ноге. На вход коленного привода поднятой ноги подавался сигнал прямоугольной формы амплитудой 0,05 рад. Записывалось входное воздействие и отклик привода при трех вариантах настройки демпфирующих обратных связей. Средний процесс получен при коэффициентах, условно принятых за единицу, верхний при увеличении коэффициентов во всех приводах в 5 раз, а нижний при их уменьшении в 4 раза. Данный опыт иллюстрирует существование оптимальной настройки и невозможность функционирования системы с данной добротностью по скорости без дополнительного демпфирования. Можно констатировать устойчивость системы к изменению настроек в широких пределах.
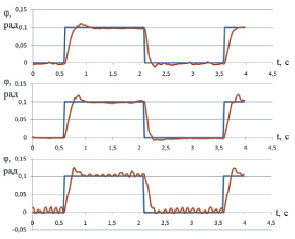
Рис. 46. Переходные процессы в коленном приводе ДШР ри различных настройках обратных связей по динамическому давлению
Также в данном методе ценно отсутствие необходимости изменять алгоритм расчетов при смене фаз движения и при изменении уравнений связей, наложенных на стопы. В исходное блочно-матричное уравнение динамики можно включить уравнения связей, наложенных сразу на обе стопы. Они будут включаться в работу при появлении соответствующих реакций, измеряемых датчиками, установленными на стопах робота. Переключение при этом происходит автоматически, без ветвления вычислительного алгоритма.