Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

ЭНЕРГОЭФФЕКТИВНЫЕ СИСТЕМЫ ГИДРАВЛИЧЕСКИХ ПРИВОДОВ ШАГАЮЩИХ МАШИН: МОНОГРАФИЯ

Семенов С. Е., Щербачев П. В., Тарасов О. И.,

Схема электрогидравлического привода с раздельным управлением группами поршней

В некоторых случаях энергоэффективность дроссельного привода можно существенно повысить за счет применения специальных схем включения и алгоритмов управления. Это может относиться как к приводам поступательного движения, так и к приводам вращательного движения. Проанализируем такой подход на примере привода вращательного движения.

Рассмотрим электрогидравлический привод с раздельным управлением группами поршней (рис. 47). Одна группа представляет собой 2 цилиндра, расположенных радиально по отношению к оси вращения выходного звена. Для функционирования такой схемы необходимо как минимум 2 группы. Группы установлены с угловым сдвигом φ0. Величина сдвига зависит от типа кинематической связи между поршнями. В качестве кинематической связи может выступать кулачек (как показано на схеме рис. 47), либо может быть использован кривошипно-ползунный механизм.

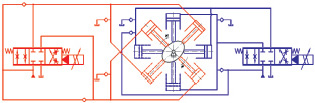
Рис. 47. Схема ЭГП с двумя группами поршней

Поршни, показанные пунктирной линией, не являются обязательными и могут быть использованы в конструкции для разгрузки вала от радиальных сил.

Каждая группа поршней управляется одним электрогидравлическим распределителем. В данном случае изображены электрогидравлические усилители. Угол сдвига φ0 выбирается так, чтобы фазы положения поршней разных групп в каждый момент времени отличались на 90°.

Для вращения выходного звена такой схемы на управляющие устройства групп должны подаваться сигналы, связанные с текущим углом поворота. Кроме того, сигналы на первый и второй распределители имеют разность фаз в 90°. Другими словами, сигналы на первый и второй распределители должны быть пропорциональный синусу и косинусу текущего угла поворота вала привода. Так, для одного распределителя

X = A∙sin(k∙(φ + φ0)),

где φ –	текущий угол поворота вала;
φ0 –	угол сдвига между группами поршней;
k –	коэффициент, задаваемый типом кинематической связи и определяющий число ходов каждого поршня за один оборот вала;
A –	амплитуда сигнала;
X  –	смещение золотника управляющего устройства.

Величина A может вычисляться различными способами в зависимости от режима работы привода [50]. В простейшем случае A – произвольно задаваемая величина. При этом отсутствует слежение по углу поворота и скорости вращения. Величина скорости определяется значением амплитуды A и внешней нагрузкой, приложенной к валу.

В случае слежения по углу поворота величину A следует вычислять следующим образом:

A = kу∙(φз – φ),

где φ –	текущий угол поворота вала;
φз –	заданный угол поворота вала;
kу –	коэффициент передачи.

В режиме отработки заданной скорости выходного звена величину A следует вычислять следующим образом:

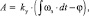
где ωз – заданная угловая скорость.

При этом по сути сохраняется слежение по углу поворота, т.к. вычисляется ошибка между текущим и увеличивающимся заданным значениями положения вала.

Рассмотрим способ управления приводом, при котором можно повысить его энергоэффективность. В схеме на рис. 47 в каждой из групп предусмотрены специальные клапаны. Два из них соединяют рабочую камеру с линией нагнетания при превышении давления в камере величины давления питания, два других соединяют поршневые полости с линией низкого давления при снижении давления в камере ниже величины давления в сливной магистрали. Таким образом, возможен возврат жидкости в линию высокого давления и зарядка гидроаккумулятора, а также заполнение рабочей камеры из сливной линии, минуя насос. Это в итоге приведет к общему снижению расхода жидкости, потребляемого приводом от насосной станции.

Для реализации описанного выше режима необходимо изменить вид сигнала, подаваемого на распределяющие устройства. При этом одновременно со снижением расхода будет ухудшаться равномерность вращения выходного вала. Возникает задача получения максимальной энергетической выгоды при минимальной неравномерности скорости вращения.

Примем следующий вид управляющего:

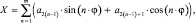
где a = {a0, a1, …, a2m} – вектор параметров.

В этом случае сигнал представляет собой сумму гармоник от 1 до m.

Для количественной оценки энергетической выгоды и равномерности скорости составим два критерия. Энергетический критерий выглядит следующим образом:

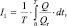
где Q –	фактический расход привода;
Qг –	геометрический расход привода.

Критерий равномерности вращения представлен в форме:

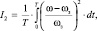
где ω –	текущая угловая скорость;
ωз –	заданная угловая скорость.

Для решения оптимизационной задачи из представленных критериев нужно составить целевую функцию f(I1, I2) и найти ее минимум. Однако вид этой функции изначально неизвестен. Добиться равной степени влияния критериев на возрастание и убывание функции не представляется возможным. В таком случае целесообразно воспользоваться методом условной оптимизации. При этом проводится поиск минимума энергетического критерия I1 при выполнении условия I2 < ε, где ε – некоторая постоянная величина.

Математическая модель привода с раздельным управлением группами поршней

Для решения задачи составлена математическая модель привода.

Уравнение движения нагрузки

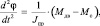
где Jпр –	приведенный к валу момент инерции нагрузки;
–	момент гидродвигателя, равный сумме моментов от каждого поршня;
Mс –	момент сопротивления.

Момент от действия одного поршня

Mп = (pп∙Sп – kв.тр∙vп)∙k∙h∙sin(k∙(φ + φ0)),

где pп –	давление в поршневой полости;
Sп –	площадь поршня;
kв.тр –	коэффициент вязкого трения пары поршень-цилиндр;
vп –	скорость поршня;
k –	число ходов каждого поршня за один оборот вала;
h –	максимальное смещение поршня.

Скорость нарастания давления в рабочей камере

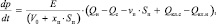
где E –	модуль объемной упругости жидкости;
V0 –	мертвый объем в цилиндре;
xп –	ход поршня;
Qн –	расход через напорную щель золотникового распределителя;
Qс –	расход через сливную щель золотникового распределителя;
Qкл.с –	расход из линии низкого давления в рабочую камеру через обратный клапан;
Qкл.н –	расход из рабочей камеры в линию высокого давления через обратный клапан.

Уравнения расходов жидкости через дросселирующие щели

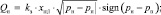
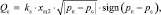
где xщ –	величина открытия щели;
pн –	давление питания гидросистемы;
pс –	авление в сливе гидросистемы;
kз –	коэффициент проводимости щели.

В модели заложена возможность изучения влияния микрогеометрии дросселирующих щелей на работу привода. Поэтому величина открытия каждой щели вычисляется с учетом перекрытий в паре
золотник-гильза, радиального зазора в паре золотник гильза и технологического радиуса скругления кромок [52].

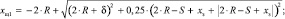
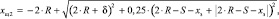
где R –	радиус скругления кромок;
Δ –	радиальный зазор в паре золотник гильза;
S –	перекрытия в паре золотник гильза;
xз –	смещение золотника.

Закон смещения золотника.

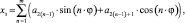
где {a0, a1, …, a2m} – вектор параметров.

Исходные данные для моделирования приведены в табл. 8.

Таблица 8

Исходные данные для моделирования

Название	Обозн.	Величина
Приведенный к валу двигателя момент инерции нагрузки	Jпр	4 кг∙м2
Эффективная площадь поршня	Sп	113,1 мм2
Коэффициент вязкого трения	kв.тр	500 Н/(м/с)
Число ходов каждого поршня за один оборот вала	k	2
Максимальное смещение поршня	h	8 мм
Модуль объемной упругости жидкости	E	1,2∙109 Па
Мертвый объем в цилиндре	V0	0,4 см3
Давление питания гидросистемы	pн	21 МПа
Давление в сливе гидросистемы	pс	0,5 МПа
Коэффициент проводимости щели	kз	6,826∙10–4 (м3/с)/(м∙Па0,5)
Радиальный зазор в паре золотник гильза	Δ	1 мкм
Перекрытия в паре золотник гильза	S	5 мкм
Радиус скругления кромок	R	6 мкм

В [52] предложен метод описания точности изготовления цилиндрического золотникового распределителя. Схема приведена на рис. 48. Основными параметрами точности являются:

S – перекрытия кромок;

R – радиусы скругления кромок;

Δ – радиальный зазор в паре золотник-гильза.

Параметры R и Δ являются приблизительно одинаковыми для всех рабочих кромок. Параметр S может достаточно сильно варьироваться в силу технологии изготовления. Поэтому при составлении математической модели следует учесть индивидуальный закон открытия каждой из дросселирующих щелей золотникового распределителя.

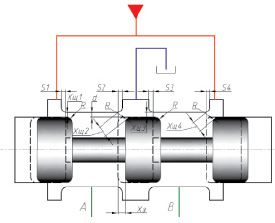
Рис. 48. Схема цилиндрического золотникового распределителя

Величины перекрытий в паре «золотник-гильза», входящие в уравнения математической модели, изначально неизвестны. Непосредственно измерить их также не представляется возможным. В таком случае для их определения целесообразно воспользоваться предлагаемым методом идентификации. Для этого необходимо определяемые величины представить набором варьируемых параметров S = {S1, S2, …, S8}. Также нужно выбрать критерий несоответствия Δ математической модели и моделируемого объекта. Идентичность модели и объекта будет достигнута при обеспечении минимума критерия Δ на множестве параметров S. Таким образом, метод идентификации параметров представляет собой задачу многомерной оптимизации. Блок-схема описанного алгоритма решения задачи представлена на рис. 49. В качестве численного метода поиска минимума был использован метод «деформируемого многогранника», известный также как метод Нелдера – Мида.

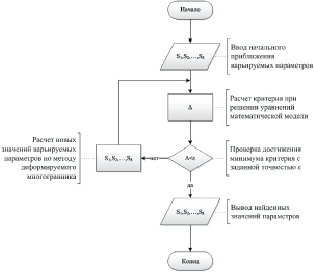
Рис. 49. Блок-схема алгоритма идентификации

Наибольшее влияние неточности изготовления золотниковых распределителей оказывают на характер изменения давлений в полостях цилиндров. Поэтому величина несовпадения давлений в полостях цилиндров, полученных экспериментально и теоретически, выбрано в качестве вышеуказанного критерия Δ.

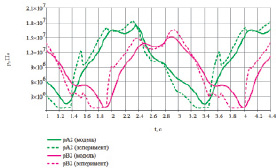
В ходе эксперимента привод работал в режиме слежения по угловой скорости вращения выходного звена. Зависимость давлений в полостях от времени, полученная экспериментально, показана на рис. 50.

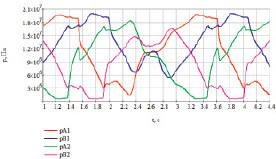
Рис. 50. Экспериментальные данные

Для иллюстрации влияния перекрытий на изменение давления на рис. 51 показаны зависимости давлений в полостях цилиндров, полученные при расчете математической модели с нулевыми значениями перекрытий.

Во время проведения эксперимента данные с датчиков давления фиксировались с частотой 1000 Гц. Критерий совпадения характеристик был получен суммированием разниц между давлением, полученным экспериментально, и давлением, полученным при моделировании, в течение одного оборота с интервалом по времени 0,001 с (рис. 52). Математическое выражение сформированного критерия следующее:

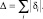
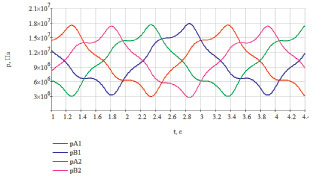
Рис. 51. Результаты моделирования

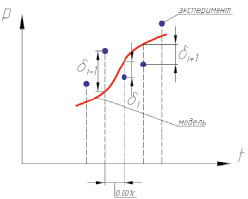
Рис. 52. Формирование критерия

Полученные в результате процедуры идентификации значения перекрытий в золотниковых парах представлены в табл. 9.

Таблица 9

Значение параметров микрогеометрии золотнике

ЭГУ 1		ЭГУ 2
Номер кромки	S, мкм	Номер кромки	S, мкм
1	8,0	1	–0,6
2	–5,4	2	19,5
3	13,8	3	–0,1
4	–5,1	4	15,1

Следует отметить, что полученные цифры показывают не только неточность изготовления золотниковых пар, но также включают в себя смещение золотника от нейтрального положения при нулевом входном сигнале – дрейф нуля ЭГУ.

На рис. 53 и 54 представлены графики изменения давлений в полостях цилиндров с учетом вычисленных значений перекрытий. Пунктирные линии отображают экспериментальные данные, сплошные – результаты моделирования.

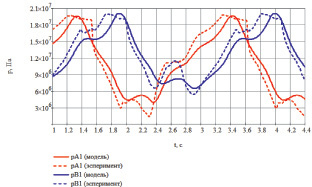
Рис. 53. Сопоставление результатов (цилиндр 1)

Рис. 54. Сопоставление результатов (цилиндр 2)

После проведения процедуры идентификации трудно измеряемых параметров, математическую модель можно считать верифицируемой. Далее с ее помощью можно синтезировать специальный закон управления для повышения энергоэффективности привода.

Для поиска условного минимума вышеописанной целевой функции был использован метод модифицированной функции Лагранжа [53]. Непосредственно процедура минимизации проводилась методом деформируемого многогранника, известного также под названием метода Нелдера – Мида.

Алгоритм расчета параметров показан на рис. 55.

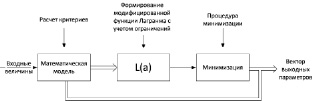
Рис. 55. Алгоритм расчета параметров

Модифицированная функция Лагранжа имеет следующий вид:

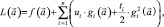
где  –	минимизируемая функция;
–	накладываемые условия типа .

В данном случае

, ,

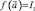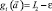где ε – требуемая величина неравномерности скорости вращения.
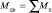
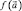
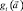
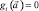