Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
Ю.В. Герасимов, Г.К. Каретников, А.Б. Селиванов. МОДЕЛИРОВАНИЕ ЗАПУСКА МАЛЫХ СПУТНИКОВ С МЕЖДУНАРОДНОЙ КОСМИЧЕСКОЙ СТАНЦИИ
Ю.В. Герасимов, Г.К. Каретников, А.Б. Селиванов
МОДЕЛИРОВАНИЕ ЗАПУСКА МАЛЫХ СПУТНИКОВ
С МЕЖДУНАРОДНОЙ КОСМИЧЕСКОЙ СТАНЦИИ
Московский государственный технический университет им. Н.Э. Баумана,
Москва, Россия
E-mail: [email protected]
Наметившаяся тенденция миниатюризации бортовой аппаратуры космических аппаратов ведет к их удешевлению. Представленное в данной работе направление развития космических систем указывает путь к поиску альтернативных технологий выведения спутников на орбиту.
В настоящее время основная часть запускаемых сегодня малых космических аппаратов массой до 10 кг (наноспутников) выводится в околоземное пространство ракетой – носителем, затем разводится по орбитам за счет реактивной тяги. Более экономичные способы выведения наноспутников – запуск с пилотируемой космической станции рукой космонавта, либо с помощью специального механизма. Первый эксперимент по ручному запуску был проведен в 2005 г.: космонавт С. Шарипов запустил с орбитальной станции МКС технологический наноспутник
ТНС-0. Таким способом осуществляется 3–5 пусков в год. Отрицательная сторона такого пуска – получаемый спутником угловой момент, величину и направление которого сложно предсказать.
Пружинный механизм способен обеспечить необходимую стабилизацию, но полученный спутником импульс – мал и неточен. Электромагнитный запуск выгодно отличается от ручного и пружинного способов пуска. Импульсный ускоритель может осуществлять пуски загруженной в него партии спутников в автономном режиме за счет возобновляемых источников энергии, с минимальным участием космонавта. Достижимые скорости с использованием пушки Гаусса –
100–1000 м/с, рельсотрона – до 4000 м/с.
Экспериментальные исследования
На базе «Центра быстропротекающих процессов» и кафедры химии МГТУ им. Н.Э. Баумана проведены экспериментальные исследования. Принципиальная электрическая схема эксперимента представлена на рис. 1, а. Конденсатор С заряжался от источника питания ? до 800–1500 В (все зависимости тока и напряжения от времени, указанные в работе, соответствуют начальному напряжению 800 В). На осциллографе С9-8 снималось падение напряжения на разряднике (Канал А) и ЭДС индукции в контуре, сцепленном с витком подводящего к рабочей части провода (Канал Б). Кинетическая энергия, которую получило метаемое тело массой 1 кг, оценивалась по отклонению от вертикали баллистического маятника. Исследования проводились в 2 вариантах: с последовательным подключением катушек и с параллельным подключением.
Цепь замыкается при пробое в воздушном зазоре разрядника К2. Использованные в экспериментальных исследованиях стационарная и подвижная катушки имеют, соответственно, длину 125 и 49 мм; внешние диаметры 45 и 19 мм; индуктивности 17,5 и 7,4 мГн, сопротивления 6,7 и 23,7 Ом. Проводились измерения: напряжение на разряднике как функция времени, скорость изменения тока в цепи, кинетическая энергия метаемого тела.
Физико-математическая модель
Динамику разгона определяют геометрические параметры двух катушек, сечение и материал провода; электроемкость батареи конденсаторов и начальный заряд; сопротивление разрядника. Перечисленные характеристики катушек задают сопротивления катушек R1, R2, индуктивности L1, L2, взаимную индуктивность L12(z), а также определяют их массы. Зависимые координаты в системе: координата подвижной катушки z(t) отсчитывается от торца стационарной, заряды q1(t) и q2(t), прошедшие через катушки. На внутреннюю подвижную катушку действует сила Ампера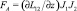 
, направление которой определяется взаимным направлением токов в катушках J1 и J2.
а б
Рис. 1. Поведение тока от времени:
а – теоретическая зависимость; б – экспериментальные данные
Согласно численному решению уравнений, проведенному в пакете Mathematica, метаемое тело приобрело скорость 0,3 м/с, что соответствует отклонению подвеса на 10°. Данное отклонение наблюдалось в эксперименте. КПД пушки определяется как отношение кинетической энергии метаемого тела к начальной энергии на конденсаторе и составил 0,1 %. Сигнал с канала Б осциллографа с точностью до коэффициента дает производную тока по времени. Первообразная от снятого сигнала приведена на графике на рис. 1, б, показывает поведение тока в цепи и находится в удовлетворительном соответствии с расчетной зависимостью на рис. 1, а. Аналогично было исследовано поведение системы с параллельным подключением катушек [1].
Выбор рациональных параметров
Исходя из экспериментальных и расчетных исследований предлагается конструкция пусковой установки, позволяющей увеличить КПД установки за счет дополнительной силы отталкивания между L2 и L3 а также оптимизировать соотношение между сопротивлениями и индуктивностями катушек. Подвижная катушка, секция I и секция II стационарной, подключены к батарее конденсаторов как показано на рис. 2. При разрядке конденсаторов токи в катушках обеспечивают втягивание подвижной катушки внутрь секции 2 и выталкивание из секции 1. В начальном положении середина подвижной катушки приходится на границу между секциями. Скорость метаемого тела варьируется напряжением на конденсаторах и ёмкостью задействованной батареи конденсаторов.
a б
Рис. 2.
а – принципиальная электрическая схема предлагаемой установки
пушки Гаусса; б – кинематическая схема метающего устройства
а
б
Рис. 3.
а – зависимость скорости метаемого тела от напряжения на конденсаторах; б – зависимость КПД установки от напряжения на конденсаторах.
Ёмкость батареи варьируется: 1 мФ, 5 мФ, 50 мФ, 100 мФ
Динамика системы определяется функцией Лагранжа и диссипативной функцией Рэлея:
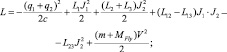
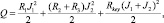
где J1 – ток через катушку L1; J2 – ток через катушки L2 и L3; масса подвижной катушки MFly определяется диаметром и длиной провода; m – масса полезной нагрузки; V – скорость подвижной катушки. Соответствующие уравнения движения – второй закон Ньютона для подвижной катушки с метаемым телом и уравнения цепи.
Численное решение системы уравнений движения в совокупности с начальными условиями в пакете Mathematica дает скорость подвижной части в зависимости от времени. Расчеты велись для установки, включающей стационарные катушки с внешним диаметром 90 мм, длиной l1 = 125 мм, l3 = 90 мм; подвижную катушку диаметром 54 мм длиной 50 мм, диаметр провода 9 мм. При достижении максимальной скорости метаемое тело отделяется от импульсного устройства.
На графиках рис. 3, а приведена зависимость скорости метаемого тела массой 1 кг от напряжения на конденсаторах при разных значениях ёмкости батареи. Полученные данные позволяют оценить эффективность использования конденсаторной батареи изменяемой ёмкости. Предложенная схема позволяет метать тела массой 1 кг со скоростью 100–600 м/с с КПД в диапазоне 11–21 %. Разработана установка, обеспечивающая метание аппарата массой 1 кг со скоростью 100–600 м/с без вращения, с минимальным разбросом по скоростям, с КПД в диапазоне 11–21 %.
ЛИТЕРАТУРА
1. Фионов А.С., Герасимов Ю.В., Селиванов А.Б. Физико-математическая модель электромагнитного ускорения наноспутников с помощью пушки Гаусса. Необратимые процессы в природе и технике: Труды V Всероссийской конференции. – М.: МГТУ им. Н.Э. Баумана, ФИАН, 2009.
2. Фионов А.С., Герасимов Ю.В., Филиппенко А.В. Варианты развития технологий ускорителей масс в космонавтике. – Необратимые процессы в природе и технике: Труды IV Всероссийской конференции, – М.: МГТУ им. Н.Э. Баумана, ФИАН, 2007 г.
3. Урличич Ю.М., Селиванов А.С., Вишняков В.М. Наноспутники – космические платформы для отработки микро- и нанотехнологий и ускорения выполнения НИОКР. – Сб. тр. V конференции «Микротехнологии в авиации и космонавтике», М., 2007.