
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
А.С. Савина, Л.Е. Слынько. ИССЛЕДОВАНИЕ СОСТАВА СОЛНЕЧНОЙ ПЛАЗМЫ С ИСПОЛЬЗОВАНИЕМ ПЕРВОГО ВАРИАЦИОННОГО ПРИНЦИПА
А.С. Савина, Л.Е. Слынько
ИССЛЕДОВАНИЕ СОСТАВА СОЛНЕЧНОЙ ПЛАЗМЫ
С ИСПОЛЬЗОВАНИЕМ ПЕРВОГО ВАРИАЦИОННОГО ПРИНЦИПА
Московский государственный технический университет им. Н.Э. Баумана, Москва, Россия
E-mail: savina_bmstu@inbox.ru
Рассмотрена методика применения первого вариационного принципа для получения равновесного состава медленного солнечного ветра и его упрощенной модели – водородно-гелиевой плазмы. Получены зависимости ряда термодинамических характеристик системы от температуры, обнаружена точка полной ионизации водородно-гелиевой плазмы. Представлены графики, построенные с помощью программы TERRA термодинамического расчета состава фаз произвольных гетерогенных систем, а также их термодинамических свойств
Известно, что состояние равновесия системы, заданное парой параметров, определяется экстремумом соответствующей характеристической функции [1–3]. Приведены все возможные случаи задания пар параметров, для которых имеются соответствующие характеристические функции, принимающие экстремальные значения в состоянии равновесия (таблица) [4].
Нижний индекс «п» у величин внутренней энергии Uп, энтальпии Iп, свободной энергии Aп, и изобарно-изотермического потенциала Gп (соответственно свободной энергии Гельмгольца и свободной энергии Гиббса) означает, что в эти величины включена энергия связей атомов
в молекуле [4]. Отыскание равновесного состава из условий экстремальности характеристических функций носит название первого вариационного принципа химической термодинамики [5]. При отыскании экстремума характеристических функций должны быть соблюдены условия, ограничивающие область изменения чисел молей компонентов.
Возможные случаи задания пар параметров
и характеристические функции,
принимающие экстремальные значения в состоянии равновесия
|
Заданные параметры системы |
Соответствующая |
Значение в равновесии |
|
S, ? |
Uп |
min |
|
S, p |
Iп |
min |
|
T, ? |
Aп |
min |
|
T, p |
Gп |
min |
|
S, Uп |
? |
max |
|
S, Iп |
p |
min |
|
T, Aп |
v |
min |
|
T, Gп |
p |
max |
|
?, Uп |
S |
max |
|
p, Iп |
S |
max |
|
?, Aп |
T |
min |
|
p, Aп |
T |
min |
А) Закон сохранения массы вещества, который можно записать в виде
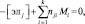 (j = 1, 2, …, m), (1)
(j = 1, 2, …, m), (1)
где [элj] – число грамм-атомов j-го химического элемента в единице массы системы (например, в 1 кг); nji – число атомов j-го элемента в i-м компоненте; k, l – соответственно число газообразных (в том числе ионизированных) и конденсированных компонентов; m – число химических элементов, образующих систему.
Б) Закон сохранения заряда (условие электронейтральности системы в целом)
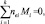 (2)
(2)
где nei – кратность ионизации; величина положительна для положительно заряженных частиц, отрицательна для отрицательно заряженных частиц и электронного газа [4].
В) Уравнение нормировки в виде уравнения состояния.
При достаточно низких давлениях и достаточно высоких температурах можно использовать уравнение состояния Менделеева – Клапейрона
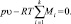 (3)
(3)
В каждом из перечисленных в таблице случаев для получения системы уравнений химического равновесия необходимо варьировать соответствующую характеристическую функцию при наложении указанных дополнительных условий. Рассмотрим наиболее часто употребляемый случай задачи: расчет при заданных T, Iп и p.
Исходное значение Iп рассчитывается по следующей формуле
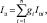 (4)
(4)
где gi – весовая доля i-го исходного вещества в системе; Iпi – энтальпия этого вещества.
Согласно таблице, для отыскания равновесного состава при заданных энтальпии и давлении следует варьировать энтропию. В силу аддитивности термодинамических функций энтропия может быть записана в виде
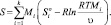 (5)
(5)
Условие постоянства энтальпии можно записать в виде
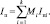 (6)
(6)
Для отыскания экстремума воспользуемся методом неопределенных множителей Лагранжа. Составляем функцию Лангранжа и берем частные производные по всем независимым переменным [4].
В итоге мы получаем окончательную систему уравнений, определяющих равновесный состав при заданных энтальпии и давлении системы:
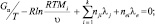 (7)
(7)
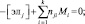 (8)
(8)
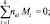 (9)
(9)
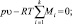 (10)
(10)
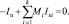 (11)
(11)
Аналогично для всех случаев задания пар параметров мы можем прийти к той же системе уравнений, за исключением последнего уравнения, определяющего задаваемый параметр. Для того, чтобы исключить эту разницу, систему можно дополнить уравнениями S = const, Uп = const, Fп = const, Aп = const:
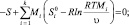 (12)
(12)
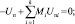 (13)
(13)
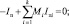 (14)
(14)
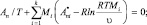 (15)
(15)
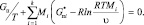 (16)
(16)
Для получения равновесного состава плазмы солнечного ветра мы воспользовались программой TERRA. В данном случае, в машину был введен относительный химический состав плазмы, давление (100 нПа) и диапазон температур 7000–21000 К. В результате чего был получен график равновесного состава плазмы в зависимости от температуры, который приведен на рис. 1. Нами были получены зависимости некоторых термодинамических характеристик водородно-гелиевой плазмы от температуры, в том числе энтропии (рис. 2), энтальпии (рис. 3) и полной внутренней энергии (рис. 4).

Рис. 1. Зависимость равновесного состава плазмы
медленного солнечного ветра от температуры

Рис. 2. Зависимость энтропии водородно-гелиевой плазмы от температуры

Рис. 3. Зависимость энтальпии водородно-гелиевой плазмы от температуры

Рис. 4. Зависимость внутренней энергии водородно-гелиевой плазмы
от температуры
Заключение
Приведено описание водородно-гелиевой плазмы в качестве упрощенной модели солнечного ветра. Показана возможность идеализации плазмы солнечного ветра. Рассмотрен алгоритм и метод первого вариационного принципа в термодинамике. Получены графики равновесного состава плазмы солнечного ветра и водородно-гелиевой плазмы, а также зависимости энтропии, полной энтальпии, полной внутренней энергии и некоторых других параметров
от температуры.
ЛИТЕРАТУРА
1. Гугенгейм Е.А. Современная термодинамика, изложенная по методу Гиббса. Л. – М., Госхимиздат, 1941, 546 с.
2. Ландау Л.Д., Лифшиц Е.М. Механика сплошных сред. – М.: Гостехтеор- издат, 1953, 467 с.
3. Румер Ю.Б., Рывкин М.Ш. Термодинамика, статистическая физика и кинетика. – М.: Наука, 1972. 589 с.
4. Слынько Л.Е. Использование термодинамических расчетов в плазмохимии // Плазмохимические реакции и процессы. – М.: Наука, 1977. – С. 164-192
5. Синярев Г.Б., Лукьянычев Ю.А., Корж С.С., Слынько Л.Е., Лохов Г.М. Химия высоких энергий, 1974, 8, № 5, 456 с.
6. Синярев Г.Б. Изв. Вузов, Машиностроение, 1965, № 2, 99.
