
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
1. Закон больших чисел. Практическое занятие по теме «Закон больших чисел»
Законы теории вероятностей получены абстрагированием статистических закономерностей массовых случайных явлений. Поэтому числовые характеристики случайных величин, такие как математическое ожидание, дисперсия, среднее квадратическое отклонение, являются предельными величинами, постоянными, к которым приближаются (сходятся по вероятности) полученные опытным путем их среднее арифметическое, дисперсия, среднее квадратическое отклонение.
Например, математическое ожидание M[X]. Оно играет наибольшую роль в теории вероятностей. Его аналогом является среднее арифметическое случайных величин.
Сравним два определения:
1. Математическим ожиданием дискретной случайной величины называется сумма произведений всех её возможных значений на соответствующие им вероятности.
2. Средним арифметическим наблюдаемых значений случайной величины называется сумма произведений её возможных значений на соответствующие им частоты.
Поясним на примерах. Если производится несколько серий опытов, то математическое ожидание есть такое постоянное число, около которого будут колебаться средние арифметические значения случайных величин, вычисленных для этих серий. Хотя и математическое ожидание и среднее арифметическое случайных величин называют средним значением.
И чем больше опытов в конкретной серии, тем меньше среднее арифметическое случайных величин отличается от математического ожидания. Именно свойство устойчивости массовых случайных явлений, величин, процессов и есть физическое содержание закона больших чисел.
В дальнейшем, по мере необходимости, различные числовые характеристики будем обозначать по-разному: математическое ожидание (М.О.) как
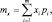 M[X];
M[X];
дисперсию как
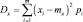 или D[X];
или D[X];
среднее квадратическое отклонение (С.К.О) как Gx или 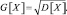
Закон больших чисел определяет условия, когда совокупное действие большого числа случайных факторов приводит к результату, практически не зависящему от случая. Эти условия и указаны в ряде теорем. Для их доказательства используется неравенство Чебышева.
