
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
1.1. Неравенство Чебышева
Вероятность того, что отклонение случайной величины X от её математического ожидания по абсолютной величине не меньше любого положительного числа ε, ограничена сверху величиной 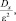 где Dx – дисперсия случайной величины X
где Dx – дисперсия случайной величины X
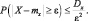
Неравенство Чебышева можно записать в эквивалентной форме
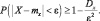
Доказательство.
1. Пусть X – дискретная случайная величина задана рядом распределения:
|
Xi |
x1 |
x2 |
…… |
xn |
|
pi |
p1 |
p1 |
…… |
p3 |
Тогда дисперсия
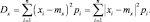
Все слагаемые этой суммы – неотрицательные. Отбросим те из них, у которых 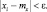 Тогда
Тогда
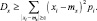
То есть суммируются только те значения i, для которых xi отклонится от mx на величину не меньше ε.
Заменим под знаком суммы 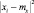 на ε2, тогда правая часть может только уменьшиться. Значит
на ε2, тогда правая часть может только уменьшиться. Значит
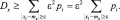
Сумма 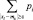 означает вероятность того, что случайная величина X отклонится от своего математического ожидания на величину ≥ ε, т. е.,
означает вероятность того, что случайная величина X отклонится от своего математического ожидания на величину ≥ ε, т. е., 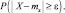
Тогда получим
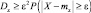
или 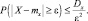
Что и требовалось доказать.
Так как
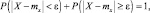
то 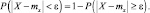
Следовательно:
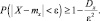
2. Пусть X – непрерывная случайная величина с плотностью распределения f(x), тогда
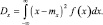
Выделим на числовой оси от mx вправо и влево отрезки длинной каждый.

Заменим интервал интегрирования (–∞; ∞) интервалом по области, лежащей вне AB, (точки А и В в отрезок не включаем.) То есть интегрирование распространяется на интервалы (–∞; mx – ε) и (mx + ε; ∞). Так как под интегралом стоит неотрицательная функция, то значение интеграла может только уменьшиться, то есть:
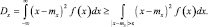
Если заменить под знаком интеграла 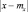 на ε, то величина интеграла может только уменьшится, то есть
на ε, то величина интеграла может только уменьшится, то есть
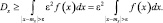
Интеграл
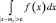
есть вероятность того, что случайная величина 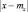 примет значение вне отрезка АВ, то есть
примет значение вне отрезка АВ, то есть 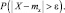 Поэтому
Поэтому
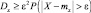 или
или 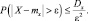
Замечание:
Знак ≥ заменен на >, так как для непрерывной величины её вероятность в точке равна 0.
Аналогично, как и в случае дискретной случайной величины, вероятность противоположного события запишется:
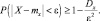
Итак, вероятность того, что отклонение случайной величины X от ее математического ожидания по абсолютной величине меньше положительного числа ε, не меньше чем 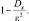
Неравенство Чебышева имеет для практики ограниченное значение, так как часто дает грубую или тривиальную оценки.
Примеры:
Пример 1.
а) Пусть 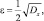
тогда 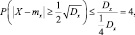
но и без этого ясно, что никакая вероятность не может быть больше 1.
б) Пусть 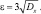 Получим:
Получим:
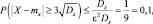
то есть вероятность того, что отклонение случайной величины X от математического ожидания выйдет за пределы трех среднеквадратических отклонений, не может быть больше  .
.
Сравним эту оценку с оценкой, полученной с помощью правила 3σ:
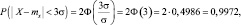
а для
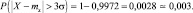
Очевидно, что оценка, полученная с помощью неравенства Чебышева, является довольно грубой.
с) Пусть 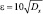 , тогда
, тогда
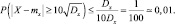
При вычислении с помощью формулы Лапласа получим:
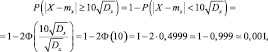
что дает меньшее расхождение результатов. То есть, неравенство Чебышева можно применять для приближенной оценки вероятности отклонения случайной величины X от ее математического ожидания только при достаточно больших ε.
Пример 2. Электрическая подстанция обслуживает сеть с 10000 ламп. Вероятность включения каждой из них вечером равна 0,6. Оценить вероятность того, что число одновременно включенных ламп, будет находиться в пределах от 5900, до 6100.
Решение: Случайная величина X – число одновременно включенных ламп. Включение каждой лампы – независимое событие, а вероятность её включения – величина постоянная. Тогда случайная величина X распределена по биноминальному закону. Поэтому её числовые характеристики:
M[X] = np = 10000∙0,6 = 6000;
D[X] = npq = 10000∙0,6∙0,4 = 2400.
Событие состоящее в том, что случайная величина X будет находиться в пределах от 5900 до 6100 означает: 5900 < X < 6100 или 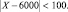 Так как для случайной величины X дисперсия ограничена, то можем применить неравенство Чебышева
Так как для случайной величины X дисперсия ограничена, то можем применить неравенство Чебышева
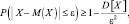
то есть 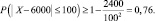
Значит, вероятность того, что число одновременно включенных ламп находящихся в пределах от 5900 до 6100, не менее 0,76.
Замечание.
Для неотрицательных случайных величин можно воспользоваться леммой А.А. Маркова.
