Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
1.6. Теорема Пуассона
Если производится n независимых опытов и вероятность появления события А в i-м опыте равна pi, то при увеличении числа опытов n разность между частотой события А и средним арифметическим его вероятностей сходится по вероятности к нулю.
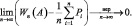
Доказательство:
Теорема Пуассона выводится из обобщенной теоремы Чебышева.
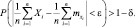
Здесь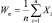 
– среднее арифметическое появления события А в 1-м, 2-м, …, n-м опытах. Случайная величина X имеет математические ожидания 
то есть
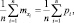
дисперсию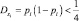 
(ограниченную). Учитывая это, теорема Чебышева примет вид теоремы Пуассона. То есть теорема Пуассона утверждает устойчивость частоты при изменяющихся условиях опыта.
Значение теоремы Пуассона в том, что на практике часто одни и те же условия не имеют шансов повториться достаточно много раз, но много раз повторяются при разных условиях, а вероятности появления события А зависят от этих условий.
Например, при игре в футбол двух спортивных команд вероятность забить гол в ворота противника зависит от разных условий (реакции футболиста, меткости удара, расстояния от ворот, скорости движения игроков и т. д.). Комплекс условий не может повторяться при забивании 2-го, 3-го и т. д. гола. Но все же имеет место устойчивость частоты забивания гола в реальных условиях. Она будет приближаться к средней вероятности забивания гола в ворота, характерной для данной группы условий.
Примеры
Пример 1. Вероятность того, что рессора через время Т эксплуатации потребует замены равна 0,4. Проверки подлежат 1000 рессор. Какова вероятность того, что отклонение доли рессор, требующих замены, от вероятности замены одной рессоры по модулю будет не больше 0,1?
Решение:
p = 0,4; q = 1 – p = 0,6; n = 1000; ε = 0,1.
Воспользуемся теоремой Бернулли:
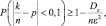
где Dx = pq = 0,4∙0,6 = 0,24, тогда
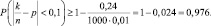
Пример 2. При запрессовке колеса на ось вероятность нарушения технологического процесса в каждом отдельном случае равна 0,2. Произведено 5000 запрессовок. Применяя теорему Бернулли, оценить по модулю величину отклонения частоты нарушении технологического процесса от вероятности нарушения его в отдельном случае, если вероятность этого отклонения не меньше 0,92.
Решение:
P = 0,92; p = 0,2; q = 1 – p = 0,8; n = 5000.
По теореме Бернулли:
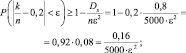
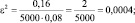ε = 0,02.
Пример 3. Во время одного из налетов фашисткой авиации на г. Сталинград было сброшено 1000 авиабомб. Вероятность того, что одна бомба поразит цель, равна 0,6. Найти:
1. Вероятность того, что модуль отклонения частоты поражения цели от вероятности поражения цели одной бомбой не превышает 0,2.
p = 0,6; q = 1 – p = 0,4; n = 1000; ε = 0,2.
По теореме Бернулли:
1. 
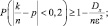Dx = pq = 0,6∙0,4 = 0,24;
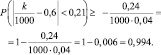
2. 
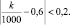
Раскроем модуль: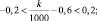 
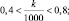400 < k < 800 то есть, интервал числа разрушенных целей составляет от 400 до 800.
Пример 4. Вероятность того, что изготовленный прибор удовлетворяет стандарту, равна 0,9. Оценить наименьшее количество приборов, которое следует отобрать, чтобы доля стандартных приборов отличалась от вероятности не более чем на 0,03, по абсолютной величине, с вероятностью не меньшей 0,85.
Решение: Пусть 
– доля стандартных приборов среди отобранных. Каждый из приборов может удовлетворить стандарту с вероятностью 0,9. Удовлетворение стандарту каждого прибора – независимое событие. Тогда можем воспользоваться теоремой Бернулли:
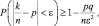
где ε = 0,03; p = 0,9; q = 1 – p = 1 – 0,9 = 0,1; P = 0,85.
Следовательно,
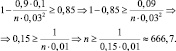
Таким образом, наименьшее количество приборов, которое следует отобрать, чтобы доля стандартных приборов отличалась от вероятности p = 0,9 не более чем на 0,03 по модулю с вероятностью не меньшей 0,85, составляет 667.