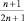Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
3. Задания для самостоятельной работы
Вариант № 1
1. В процессе эксплуатации в течение года вагон может выйти из строя с вероятностью 0,03. Какова вероятность того, что после эксплуатации в течение года 10000 вагонов отклонение частоты их выхода из строя от вероятности выйти из строя одному вагону по модулю не превысит 1 %?
2. На товарный двор поступили 20 автопогрузчиков. Вероятность наличия дефекта на каждом из них равна p = 0,1. Какова вероятность того, что 3 автопогрузчика окажутся с дефектом?
Вариант № 2
1. На погрузочной станции вагоны с однородным грузом проходят повторное взвешивание. Из 30 вагонов 6 оказываются перегруженными. Какова вероятность того, что из 800 вагонов, проходящих контрольное взвешивание, отклонение по модулю частоты их перегруза от вероятности оказаться перегруженным одному вагону не превосходит 3 %?
2. Исследуется партия из 1000 конденсаторов. Вероятность конденсатору оказаться с дефектом равна p = 0,02. В каких границах окажется число бракованных изделий в партии, если вероятность их появления равна 0,997.
Вариант № 3
1. Цех поставляет грузы для сборки агрегатов, причем при контроле из 120 узлов 2 оказываются нестандартными. Сколько надо отобрать узлов, чтобы вероятность отклонения, по модулю, частоты появления среди них нестандартных узлов, от вероятности оказаться нестандартным одному узлу, не превышающая 1 %, равнялась бы 0,9?
2. В вагоноремонтный цех поступили колесные буксы. Вероятность наличия брака у каждой из них p = 0,03. Для контроля отбирают 600 букс. Найти вероятность того, что частота появления бракованной буксы отличается от вероятности брака для каждой буксы по модулю меньше, чем на 0,01.
Вариант № 4
1. Кассир, обслуживая пассажира, может допустить ошибку с вероятностью 0,1. На какую величину, по модулю, окажется равным отклонение частоты, совершённой кассиром ошибки при обслуживании 150 пассажиров от вероятности ошибки при обслуживании одного пассажира, если допустимая вероятность отклонения равна 0,94?
2. Завод выпускает партию электроламп в 1000 шт. Вероятность того, что лампа окажется стандартной p = 0,8. Найти границы количества стандартных ламп, гарантируемых заводом с надежностью 0,9998.
Вариант № 5
1. Завод поставляет заказчику 400 рессор. Вероятность того, что каждая рессора окажется стандартной, равна 0,8. На какую величину допустимо отклонение, по модулю, частоты стандартных изделий в выпускаемой партии от вероятности каждой рессоры оказаться стандартной, если вероятность этого отклонения должна быть 0,96?
2. Для запрессовки колес на ось в колесный цех вагоноремонтного завода за время Т поступает 30 партий колес. Индикатор пресса записывает диаграмму, по которой устанавливает качество запрессовки. Математическое ожидание недопустимого отклонения от нормы в среднем в партии равно 5, а среднее квадратическое отклонение G = 3. Какова вероятность того, что за это время будет забраковано от 140 до 160 колес?
Вариант № 6
1. Железнодорожный состав состоит из 30 вагонов с углем. Вес каждого в тоннах – случайная величина с математическим ожиданием mx = 75 т. Локомотив может вести вес, не более q = 15000 т. Если вес состава окажется больше, придется присоединять второй локомотив. Найти вероятность того, что понадобится второй локомотив.
2. Завод-изготовитель поставляет на предприятие лампы дневного света. Вероятность того, что лампа окажется с дефектом, равна 0,1. Сколько надо закупить ламп, чтобы с вероятностью 0,96 отклонение числа стандартных ламп от их математического ожидания по модулю не превышало 3-х штук.
Вариант № 7
1. Вероятность p изготовления клина автосцепки, удовлетворяющего стандарту, равна 0,85. Оценить наименьшее их количество, которое следует отобрать, чтобы доля стандартных клиньев отличалась по модулю от вероятности p не больше, чем на 0,05 с вероятностью 0,85.
2. Кассир железнодорожной кассы обслуживает 90 очередей за время Т. Математическое ожидание ошибки для одной очереди равно двум, а среднее квадратическое отклонение одному. Кассир получает премию, если вероятность неверно оформленных билетов не превышает 0,2. В каких пределах в этом случае должно находиться количество неверно оформленных билетов?
Вариант № 8
1. Сборочный цех заказывает резиновые шайбы для сборки изделий. Начиная с какого количества их надо заказать, чтобы обеспечить бесперебойную качественную сборку, если известно, что вероятность для шайбы оказаться бракованной равна 0,2, а вероятность отклонения частоты появления бракованных шайб в партии от вероятности шайбе оказаться бракованной по модулю не превышает 0,1, с вероятностью 0,97.
2. На экспорт отправляется 160 составов с мясом. Математическое ожидание повреждения для одного состава за время следования составляет 4 вагона, среднее квадратическое отклонение G = 1. Какова вероятность того, что в пути будет повреждено от 600 до 650 вагонов?
Вариант № 9
1. В течение времени Т эксплуатации железнодорожного полотна вероятность p отклонения величины стыковочного зазора от стандарта равна 0,04. Какова вероятность того, что из 500 наудачу выбранных зазоров частота их отклонения от вероятности p не превысит по модулю 0,02?
2. Вагоноремонтному заводу для ремонта вагонных букс требуются запасные части двух видов. Они закупаются в количестве по 1000 штук каждого вида. Причем вероятность оказаться стандартным изделию первого вида равна 0,8, а изделию 2-го вида – 0,82. Какова вероятность того, что число стандартных изделий каждого вида будет находиться в пределах от 790 до 810 штук?
Вариант № 10
1. Станок изготавливает 10000 шарикоподшипников. Вероятность отклонения размера одного подшипника от стандарта равно p = 0,2. Каково отклонение относительной частоты события от его вероятности p, по модулю, если вероятность этого отклонения равна 0,988?
2. Городской автобус каждые 10 минут подходит к железнодорожному вокзалу. На остановку приходят пассажиры с прибывающих электричек. 36 пассажиров заходят в очередной подошедший автобус. Какова вероятность того, что суммарное время ожидания ими автобуса не менее 2,5 часов?
Вариант № 11
1. Из 1000 студентов 600 светлоглазых. Найти вероятность того, что из 400 отобранных наудачу студентов доля светлоглазых будет отличаться от вероятности студенту оказаться светлоглазым, по модулю, не больше, чем на 0,05.
2. Предприятие должно выплатить зарплату своим работникам за изготовленную продукцию. Заказчики продукции оплачивают предприятию в среднем по 200 000 рублей со средним квадратическим отклонением 50 000 рублей. Найти вероятность того, что суммы, полученной предприятием от 30 заказчиков не хватит для выплаты зарплаты всем работникам, если общий фонд зарплаты должен составлять 5 500 000 рублей.
Вариант № 12
1. На сортировочную станцию в среднем в день прибывают 10 составов. Оценить вероятность того, что в наудачу названный день прибудет не более 20 составов для сортировки.
2. Рыбак свободное время проводит на рыбалке. Вероятность того, что за время одного посещения рыбалки он поймает 7, 8, 9, 10 рыб, соответственно равна 0,4; 0,3; 0,2; 0,1. Найти вероятность того, что за 25 дней он поймает от 220 до 230 рыб.
Вариант № 13
1. На товарный двор поступают контейнеры для дальнейшего использования. Среднее число непригодных из них равно трём. Оценить вероятность того, что из 50 поступивших контейнеров более 5 окажутся непригодными.
2. Баскетболист за время игры может забросить мяч в корзину 4 раза с вероятностью 0,1; 3 раза – 0,2; 2 раза – 0,3; и один раз с вероятностью 0,4. За спортивный сезон он 30 раз участвует в соревнованиях. Какова вероятность того, что за сезон он забросит мяч в корзину от 50 до 80 раз?
Вариант № 14
1. За сутки по тракту мимо пункта N проходит 500 машин. Найти вероятность того, что в следующие сутки по тракту пройдёт не менее 600 машин.
2. Студент должен решить 20 примеров по математике. На решение одного у него может уйти от 5 до 15 минут. Считая для каждого примера все значения времени равновозможными, оценить вероятность того, что студент потратит на решение примеров не более 210 мин.
Вариант № 15
1. На складе в течение времени Т хранится 3000 электроламп. Вероятность для каждой лампы за это время выйти из строя равна 0,125. Найти вероятность того, что в непригодном состоянии окажется более 500 ламп (неравенство Маркова).
2. Вероятность истребителю сбить вражеского бомбардировщика в бою равна p = 0,75. Истребитель участвовал в 10 независимых друг от друга воздушных боях. Какова вероятность того, что на его счету будет 8 сбитых бомбардировщиков?
Вариант № 16
1. На предприятии контролируют диаметры выпускаемых шарикоподшипников. Среднее квадратическое отклонение их размера составляет 0,2 мм. Какова вероятность того, что величина диаметра наудачу взятого подшипника отличается от его математического ожидания, по модулю, более, чем на 1 мм?
2. Завод поставляет заказчику изделия, 70 % из которых высшего качества. Изделия поставляются 30 партиями по 3 изделия в каждой. Наудачу для контроля берется одна партия. Какова вероятность того, что из 30 партий высшими качествами будут обладать от 60 до 70 изделий?
Вариант № 17
1. В механическом цехе изготавливают 1000 болтов. Вероятность того, что болт стандартный p = 0,8. Оценить вероятность того, что из 1000 болтов от 700 до 900 включительно будут стандартными.
2. На пути следования локомотива на участке АВ расположено 5 светофоров. Вероятность появления красного цвета на одном из них равна 
Поезд должен проследовать через 10 таких участков. Найти вероятность того, что число остановок локомотива отличается от их математического ожидания для одного участка по модулю не более, чем на 0,2.
Вариант № 18
1. Проверяются стыковочные зазоры между рельсами. Величина этого зазора – случайная величина X. Дисперсия величины зазора D[X] = 0,5 см2. Найти вероятность того, что , где mx – математическое ожидание величины зазора.
2. Электроцех закупает электроизмерительные приборы. Завод- изготовитель поставляет 60 % приборов 1 сорта, а остальные – 2-го. Определить, сколько надо взять приборов, чтобы с вероятностью 0,997 можно было утверждать, что доля первосортных среди них будет отличаться от вероятности изготовления первосортного прибора по модулю не более, чем на 0,04?
Вариант № 19
1. Стрелок производит выстрелы по мишени. Число попаданий в мишень – случайная величина X. Вероятность того, что модуль разности Х и его математического ожидания M[X] больше M[X], меньше чем 0,3: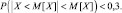 
Оценить величину математического ожидания случайной величины X, если её дисперсия D[X] = 10.
2. Из 10 тяговых двигателей, 3 не выдерживают нагрузки и выходят из строя. Какова вероятность того, что из 20 тяговых двигателей, 6 не выдержат нагрузки?
Вариант № 20
1. Пешеход проходит расстояние АВ со средней скоростью 7 км/ч и средним квадратическим отклонением 0,3 км/ч. Оценить величину отклонения скорости прохождения пешеходом участка АВ от её средней скорости, по модулю, если вероятность этого отклонения не более 0,9.
2. Механический цех выпускает болты для сборки агрегата. Вероятность появления брака при изготовлении каждого болта равна p = 0,2. Сколько надо отобрать болтов, чтобы с вероятностью 0,994, отклонение доли бракованных болтов в отобранной партии от по модулю, было не более 0,04?
Вариант № 21
1. На товарный двор для отправки заказчику поступили доски длинной X, м, c дисперсией D[X] = 0,5 м2. Вероятность того, что случайная величина X отклонится от её математического ожидания по модулю не меньше чем на величину ε, равна 0,2. Найти величину этого отклонения (ε).
2. Лампа имеет срок службы от 200 до 220 часов. Какова вероятность того, что 50 ламп поочередно будут освещать помещение не менее 10 600 часов, если время горения каждой лампы в указанном интервале равновозможно?
Вариант № 22
1. Цех изготавливает клеммные болты для крепления рельсов к шпалам в количестве 10000 штук за время Т. Вероятность брака для одного болта равна 0,15. Найти вероятность того, что число бракованных болтов среди изготовленных будет заключено в интервале от 1000 до 2000 включительно.
2. В районе среди 1000 жителей, проживает 520 русских. Найти вероятность того, что среди 600 наудачу выбранных жителей, доля русских будет отличаться от вероятности жителю оказаться русским, по модулю, меньше, чем на 0,03?
Вариант № 23
1. Среднее квадратическое отклонение каждой из 2500 независимых случайных величин X не превосходит 3. Оценить вероятность того, что абсолютная величина отклонения средней арифметической случайной величины X от средней арифметической их математических ожиданий, не превзойдет 0,3.
2. Цех выпускает 75 % изделий высшего качества. Какова вероятность того, что из 100 партий таких изделий, от 20 до 30 изделий окажутся не высшего качества?
Вариант № 24
1. К потребителю поступает большой заказ с заготовками. Выборочным путем определяют их среднюю длину. Сколько надо обследовать заготовок, чтобы с вероятностью больше 0,9 можно было утверждать, что средняя длина отобранных изделий будет отличаться от среднего значения их математических ожиданий по модулю не больше, чем на 0,001 см. Установлено, что среднее квадратическое отклонение длины заготовки не превышает 0,04 см.
2. Нарушение связи диспетчера с машинистом локомотива, может произойти с вероятностью 0,2. Сколько раз будет нарушена связь при 100 коммуникациях, если нарушение связи может ожидаться с вероятностью 0,0508?
Вариант № 25
1. Последовательность независимых случайных величин X1, X2, ..., Xn задана законом распределения.
|
Xn |
a |
–a |
|
p |
|
|
Применима ли к данной последовательности теорема Чебышева?
2. 60 % контейнеров, прибывших на грузовую станцию, оказались поврежденными. Наудачу выбрали 200 контейнеров. Чему равна вероятность того, что среди них поврежденными окажутся:
а) от 120 до 150;
б) от 90 до 150?
Вариант № 26
1. Вероятность того, что при опускании одного жетона автомат сработает правильно, равна 0,95. Найти минимальное число жетонов при опускании которых в игральный автомат, частота правильной работы автомата была бы заключена в границах от 0,93 до 0,97 включительно, с вероятностью не меньше 0,93. (Применить неравенство Чебышева).
2. Работница обслуживает 800 веретён. Вероятность обрыва пряжи на каждом из них за время t, равна 0,005. Найти среднее число обрывов и его вероятность, применяя локальную теорему Муавра – Лапласса.