Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
§ 1.1. Переход от классической физики к квантовой
Современная физика началась с открытия М. Планком квантования излучения, с гипотезы Л. де-Бройля о наличии у электронов волновых свойств с длиной волны, равной λD = h/p, а так же с полуклассической теории атома водорода, предложенной Н. Бором.
Применяя эти результаты к атомной системе – атому водорода, как следствие, получим:
а) стационарное состояние атома характеризуется стационарным волновым процессом, определяющим движение электрона.
б) стационарный волновой процесс устойчив, если на определенной длине укладывается целое число длин волн – образуется «стоячая волна».
в) в атоме длина пути электрона по орбите равна Ln = 2πrn и при движении электрона на ней образуется стоячая волна де-Бройля. Тогда имеем: 2πrn = nλD. Откуда следует, что «орбиты квантуются».
Если траектория длиной Ln замкнута и не обязательно является окружностью, то можно записать:
.
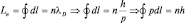Последнее равенство приводит к квантовому постулату Бора: «момент импульса квантован».
Оставался неясным вопрос о реальности волн де-Бройля. Действительно ли движению частиц вещества сопутствует волновой процесс? На этот вопрос отвечают эксперименты, проведенные вначале Дэвиссоном и Джермером (с электронами), а затем Томсоном (младшим) и Штерном (с молекулярными пучками). Электроны, ускоренные электрическим полем, получали энергию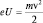 
и были направлены на поликристалл Ni (с периодом решетки d). На экране при этом, наблюдается картина дифракции, соответствующая длине волны λ (по Вульфу-Брэггу 2dsin θ = nλ). С другой стороны, эта длина волны может быть рассчитана по формуле де-Бройля
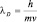или 
.
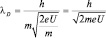Расчет полностью совпал с результатами эксперимента.
Таким образом, было доказано наличие у электронов (а затем у ионов, и молекул) волновых свойств.
Положительные результаты экспериментов по выявлению волновых свойств, сразу же поставили вопрос о природе волн де-Бройля.
Какие здесь были возможны ва рианты?
1. Если эти волны подобны электромагнитным, то им соответствует особая материальная субстанция (поле) как объективная реальность. Тогда эти «волны материи» (по де-Бройлю) способны переносить на себе частицу, аналогично тому, как обычные волны на поверхности воды «подталкивают» пробку, щепку и т.п., либо так, как воздушная среда «поддерживает» планер в полете. Отсюда возникла первая модель «волны-пилота», переносящей элементарную частицу. В этом случае волны можно «оторвать» от частицы и наблюдать их отдельно, но именно этого никак не удается сделать экспериментально.
2. Тогда возникла другая модель частицы как о «сгустке» волн или «волновом пакете». Как же образуется волновой пакет? Так как ниже будет часто употребляться термин «волна», в начале, следует подробнее представить ее математический образ.
Возьмем за основу электродинамику (в вакууме) и запишем исходные уравнения Максвелла, а затем применим операцию ротора к левой и правой части первого уравнения:
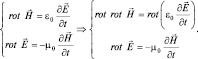(1.1.1)
Из векторного анализа (теории поля) известно, что
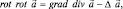
где Δ – оператор Лапласа (в декартовой системе координат он сумме операций: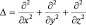 
). Поэтому в первом равенстве системы уравнения Максвелла имеем: 
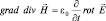(операции дифференцирования по времени и ротора можно менять местами, так как эти переменные – координаты и время – независимы). Но в вакууме 
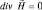, поэтому имеем:
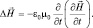
В скобке для замены электрического поля на магнитное использовано 2-е уравнение Максвелла из системы (1.1.1). После преобразований, в случае одномерного движения, окончательно имеем уравнение:
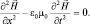(1.1.2)
Его решением является функция вида:
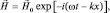(1.1.3)
которая, при t = 0, характеризует стационарную волну в пространстве: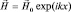 
, а в точке, при x = 0, колебательный процесс: 
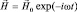. Таким образом, по смыслу, функция 
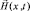в выражении (1.1.3) совпадает с определением волнового процесса в физике, а поэтому может быть названа волновой функцией. Уравнение (1.1.2) по той же причине называют уравнением волны. Если записать волновую функцию в тригонометрической форме (по Эйлеру): 
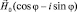, то, в простейшем варианте, можно ограничиться лишь действительной (наблюдаемой) частью. Окончательно, произвольную волновую функцию Ψ запишем в виде:
Ψ = Ψ0cos φ,
где Ψ0 – амплитуда, а φ – фаза волны.
Теперь, вновь возвращаясь к модели «волнового пакета», сложим две волны
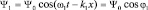и 
с близкими по величине частотами и длинами волн:
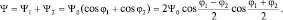
Отдельно рассмотрим сумму и разность фаз:
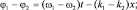
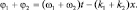
Так как частоты (и длины волн близки), то можно приближенно считать, что ω1 + ω2 ≈ 2ω1; k1 + k2 ≈ 2k1; ω1 – ω2 ≈ Δω; k1 – k2 ≈ Δk, где Δω и Δk малы по сравнению с ω1 и k1. После подстановки полученных выражений в сумму волн имеем:
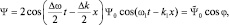(1.1.4)
что на графике может быть представлено как произведение (модуляция) двух волн, одна из которых характеризуется частотой ω = ω1 и волновым числом k = k1, а другая малой частотой Δω и волновым числом Δk (рис. 1, слева).
Рис. 1. Формирование волнового пакета
Образуются «биения», как говорят об этом в физике колебаний. Легко проверить математически (составив программу на компьютере), что при сложении большого числа волн с близкими по величине частотами, результирующая волна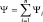 
будет выглядеть так, как это изображено на рис. 1 (справа). Образующийся «сгусток» из группы волн был назван «волновым пакетом». Таким образом, волновой пакет – это сложное образование, движение которого может быть охарактеризовано двумя скоростями:
а) скоростью движения отдельной волны в группе – vф (фазовая скорость);
б) скоростью движения максимума – амплитуда группы волн – vгр (групповая скорость).
Из этих определений видно, что математически фазовая скорость может быть вычислена, если зафиксировать фазу волны φ, а групповая, если считать фиксированной амплитуды 
. Другими словами:
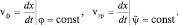(1.1.5)
Расчет этих величин приводит к следующим результатам:
а)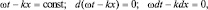 
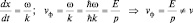(1.1.6)
b)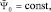 
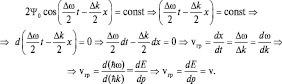(1.1.7)
Вывод: групповая скорость пакета, действительно, совпадает со скоростью движения самой частицы, но фазовая скорость зависит от длины волны, что приводит к «размыванию» пакета со временем, как если бы, в группе бегущих спортсменов одни стали «опережать» других. Поэтому «сгусток» волн не может заменить стабильную во времени частицу. В то же время, как нам известно, электроны, летящие от Солнца, достигают Земли, не размываясь. Время размывания волнового пакета для волн, с фазовой скоростью vф оценивается величиной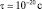 
, а время движения электронов от Солнца к Земле 
.