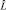Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
§ 1.3. Математический аппарат квантовой механики
Задача поиска уравнения движения микрообъекта, в сущности, представляла собой проблему разработки математического аппарата, адекватно отражающего все известные особенности поведения частиц в микромире («квантовые скачки», линейчатые спектры, дискретные уровни энергий и т.д.).
Вначале проведем анализ одного из первых предположений: свободному движению электрона сопутствует волновой процесс. В этом случае электроны в пучке могут быть ускорены стационарным электрическим полем и при этом – что сейчас для нас важно – ведут себя подобно классическим (заряженным) частицам, т.е. способны воспринять любую энергию без всяких квантовых скачков. Как это отражается в математической модели? Имеем волновое уравнение: 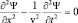 и его решение в виде волновой функции
и его решение в виде волновой функции 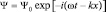 или
или 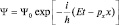 . Избавимся от второй производной по времени подстановкой
. Избавимся от второй производной по времени подстановкой 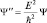 в волновое уравнение. Получим следующее уравнение (обозначим его буквой А):
в волновое уравнение. Получим следующее уравнение (обозначим его буквой А):
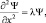
где 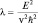 .
.
Решением этого уравнения является функция 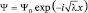 . При этом, λ обязана быть величиной положительной на интервале [0, ∞) и величина энергии E также может принимать все возможные значения в интервале [0, ∞). Никакой дискретности! Если же λ < 0, то мнимая величина
. При этом, λ обязана быть величиной положительной на интервале [0, ∞) и величина энергии E также может принимать все возможные значения в интервале [0, ∞). Никакой дискретности! Если же λ < 0, то мнимая величина 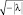 может быть представлена как
может быть представлена как 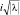 , а тогда при стремлении координат к бесконечности, (х → ∞), функция
, а тогда при стремлении координат к бесконечности, (х → ∞), функция 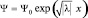 также стремится к бесконечности, что физически не определено.
также стремится к бесконечности, что физически не определено.
Движение электрона в атоме стало ограничено: если координаты r = const и θ = const, то φ – периодична. Если электрон попал через некоторое время в ту же точку, то его состояние должно остаться тем же (требование однозначности).
Это возможно в том случае, когда 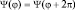 . Сохраняя вид правой части волнового уравнения и вид решения, имеем:
. Сохраняя вид правой части волнового уравнения и вид решения, имеем:
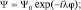
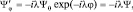
а тогда получим новое уравнение (обозначим его буквой В): 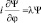 .
.
Решением уравнения (В) является, функция 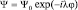 , при условии, что
, при условии, что 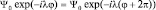 . Тогда
. Тогда  , откуда
, откуда  . Расписывая левую часть по формуле Эйлера, получаем:
. Расписывая левую часть по формуле Эйлера, получаем: 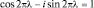 . Это возможно лишь тогда, когда в левой части отсутствует мнимое число, а поэтому
. Это возможно лишь тогда, когда в левой части отсутствует мнимое число, а поэтому  и
и  , поэтому λ = 0, ±1, ±2, ..., т.е. принимает дискретный ряд значений.
, поэтому λ = 0, ±1, ±2, ..., т.е. принимает дискретный ряд значений.
Если по-прежнему считать, что величина λ связана с энергией, то энергия становится «квантованной». Оба уравнения: (А) и (В) могут быть объединены единой формой записи: дифференцирование некоторой функции Ψ равно самой функции, умноженной на измеряемую физическую величину λ, что можно представить следующим образом:  . Такая форма записи позволяет перейти к введению понятия оператора.
. Такая форма записи позволяет перейти к введению понятия оператора.
Определим оператор как всякое действие (а также символ, обозначающий это действие), ставящее в соответствии одной величине другую (например: функциональная зависимость, ее конкретное выражение, взятие производной, умножение на число, умножение на матрицу и др.).
Возвращаясь к примерам (2.1.1) и (2.1.2) и используя понятие оператора, запишем два оператора в виде: 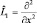 и
и 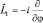 .
.
В обоих случаях в правой части уравнений (2.1.1) и (2.2.2) получается один и тот же результат: вид функции, умноженной на величину λ, сохраняется. Полученный оператор 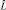 (читается «L со шляпой»), который действует на функцию с сохранением ее вида так, что
(читается «L со шляпой»), который действует на функцию с сохранением ее вида так, что  , является линейным оператором. При этом функция, для которой выполняется соотношение, взятое в рамку, называется собственной функцией оператора
, является линейным оператором. При этом функция, для которой выполняется соотношение, взятое в рамку, называется собственной функцией оператора 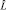 , а величина λ – собственным значением оператора, соответствующим собственной функции. Знание оператора, как мы уже видели, позволяет, решив соответствующее уравнение, найти собственную функцию и вычислить спектр собственных значений. Считаем, что вычислениям в математике соответствует измерения в физике; оператору, позволяющему вычислить собственное значение, соответствует операция измерения физической величины, а собственная функция – функция состояния системы. Уравнение, связывающее все определенные величины, функции и операторы, представляет собой уравнение движения (эволюции) системы. Представим окончательно полученную информацию в виде табл. 1.
, а величина λ – собственным значением оператора, соответствующим собственной функции. Знание оператора, как мы уже видели, позволяет, решив соответствующее уравнение, найти собственную функцию и вычислить спектр собственных значений. Считаем, что вычислениям в математике соответствует измерения в физике; оператору, позволяющему вычислить собственное значение, соответствует операция измерения физической величины, а собственная функция – функция состояния системы. Уравнение, связывающее все определенные величины, функции и операторы, представляет собой уравнение движения (эволюции) системы. Представим окончательно полученную информацию в виде табл. 1.
Таблица 1
Соотношение между физической математической моделями
|
Физическое описание микромира |
Математическая модель |
|
измеряемая величина (наблюдаемая) |
линейный оператор |
|
набор значений измеряемой величины |
собственные значения (спектр) |
|
состояние, определяемое волновой функцией Ψ |
собственная функция Ψ оператора |
|
эволюция системы (нерелятивистское приближение) |
уравнение движения (нестационарное уравнение Шредингера) |
|
эволюция системы (релятивистское движение) |
уравнение движения (уравнение Дирака) |
|
стационарное состояние |
стационарное уравнение Шредингера |
Рассмотрим, какие дополнительные требования к операторам, функциям состояния (собственными функциями) и величинами (собственными значениями) необходимо использовать исходя из «физических соображений».
1. Собственные значения величины λ должны быть вещественными, так как измеряемые на опыте физические величины всегда вещественны. Математически это требование можно записать следующим образом: λ = λ* где знак (*) обозначает комплексное сопряжение. Действительно, если λ = a + bi, а λ* = a – bi, то равенство λ = λ* или a + bi = a – bi возможно лишь при b = 0, а тогда λ = λ*, т.е. представляет собой действительное число.
2. Первое требование ограничивает класс линейных операторов, которые могут быть использованы в квантовой механике. Дело в том, что действительными собственными значениями обладают только самосопряженные операторы, удовлетворяющие следующему равенству:
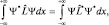 (1.3.1)
(1.3.1)
где x – произвольный параметр состояния, а Ψ* – функция состояния комплексно сопряженная исходной Ψ-функции. Действительно, если  , а
, а  , то условие самосопряженности приведет к следующему выводу:
, то условие самосопряженности приведет к следующему выводу:
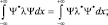
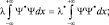
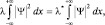
т.е. λ = λ* для каждого конкретного значения λ. Если λ = λ(x), то
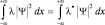
откуда, 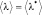 , что также возможно, только если λ – вещественная величина.
, что также возможно, только если λ – вещественная величина.
3. Собственная функция Ψ оператора 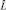 должна удовлетворять требованиям существования производных, должна быть непрерывна, однозначна и конечна (стандартные условия). Так как Ψ-функция определяет функцию плотности вероятности, то
должна удовлетворять требованиям существования производных, должна быть непрерывна, однозначна и конечна (стандартные условия). Так как Ψ-функция определяет функцию плотности вероятности, то 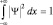 . (условия нормировки). Именно это требование использовано в предыдущем пункте. Если считать, что объект находится в реальном пространстве, то вероятность его обнаружения должна обращаться в нуль при координатах x → ±∞, т.е. Ψ(x) → 0 при
. (условия нормировки). Именно это требование использовано в предыдущем пункте. Если считать, что объект находится в реальном пространстве, то вероятность его обнаружения должна обращаться в нуль при координатах x → ±∞, т.е. Ψ(x) → 0 при 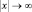 . Бесконечно удаленная от нас микрочастица как бы не существует.
. Бесконечно удаленная от нас микрочастица как бы не существует.
4. Операторы можно складывать, т.е. существует такой оператор 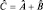 , который означает, что производится либо измерение собственной величины оператора
, который означает, что производится либо измерение собственной величины оператора  , либо собственной величины
, либо собственной величины 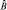 . В этом случае порядок измерений роли не играет. Операторы
. В этом случае порядок измерений роли не играет. Операторы  и
и 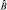 можно умножать, т.е. существует такой оператор
можно умножать, т.е. существует такой оператор 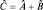 , который означает, что производится одновременное (совместное) измерение в одном и том же эксперименте
, который означает, что производится одновременное (совместное) измерение в одном и том же эксперименте  собственного значения операторов
собственного значения операторов  и
и 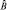 . При этом очевидно, что если измерения
. При этом очевидно, что если измерения  и
и 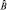 не являются независимыми, т.е. результат измерения
не являются независимыми, т.е. результат измерения 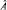 зависит от того произведено
зависит от того произведено 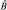 или нет, то порядок измерений как и порядок вычислений играет существенную роль. Если
или нет, то порядок измерений как и порядок вычислений играет существенную роль. Если  , то говорят, что операторы
, то говорят, что операторы  и
и 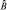 коммутативны, а если
коммутативны, а если 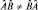 , то операторы некоммутативны (не перестановочны). Оператор (
, то операторы некоммутативны (не перестановочны). Оператор ( ) называется коммутатором:
) называется коммутатором:
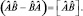 (1.3.2)
(1.3.2)
Проверить коммутативность или не коммутативность операторов  и
и 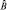 можно, если они имеют общую собственную функцию. Таким образом, если функция состояния найдена, то имеет смысл выяснить расчетным путем, какие переменные можно измерить одновременно, а какие нельзя.
можно, если они имеют общую собственную функцию. Таким образом, если функция состояния найдена, то имеет смысл выяснить расчетным путем, какие переменные можно измерить одновременно, а какие нельзя.

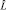 величины λ
величины λ