
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
§ 1.6. Квантовомеханические модели. Свободное движение микрообъекта и частица в потенциальном ящике
1. Рассмотрим первую задачу квантовой механики о свободном движении микрообъекта.
Условия задачи: U(x) = 0 (внешнее поле отсутствует), 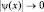 при x → 0. Запишем уравнение Шредингера:
при x → 0. Запишем уравнение Шредингера:
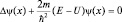 ,
,
но U(x) = 0 и 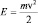 , а тогда в одномерном случае, имеем:
, а тогда в одномерном случае, имеем:
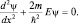
Решением уравнения является функция 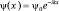 , где
, где 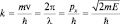 , что можно проверить простой подстановкой.
, что можно проверить простой подстановкой.
Вычислим теперь амплитуду ψ0, чтобы полностью определить функцию состояния, для чего воспользуемся условием нормировки:
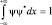 или
или 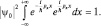
Видно, что интеграл расходится, а это значит, что нарушается условие нормировки. Необходимо вычислить нормирующий множитель:
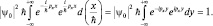
Если мы вычисляем 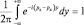 , то, как известно из курса анализа, этот интеграл принимает значение так называемой δ-функции:
, то, как известно из курса анализа, этот интеграл принимает значение так называемой δ-функции: 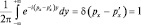 при
при  . В нашем примере, можно записать:
. В нашем примере, можно записать:
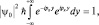
откуда 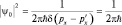 , а поэтому
, а поэтому 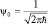 . Окончательный вид волновой ψ-функции (плоской волны) запишем следующим образом:
. Окончательный вид волновой ψ-функции (плоской волны) запишем следующим образом:
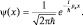 (1.6.1)
(1.6.1)
2. Задача о частице в бесконечно высоком потенциальном «ящике». Начертим график потенциального «ящика» (рис. 9). Механическим аналогом является движение частицы между двумя абсолютно упругими стенками: упругое взаимодействие «включается» только в точках x = 0 и x = l.
Условия:
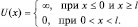
Рассмотрим стационарное движение частицы, т.е. когда E(t) = const. Запишем уравнение Шредингера для областей x ≤ 0 и x ≥ l, где U(x) =: 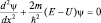 или
или 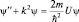 , или
, или 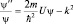 . Так как k ≠ ∞, то
. Так как k ≠ ∞, то 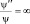 . Это возможно только тогда, когда ψ(x) = 0, а следовательно, величина
. Это возможно только тогда, когда ψ(x) = 0, а следовательно, величина 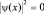 . Частицу нельзя обнаружить с координатой x ≤ 0 и x ≥ l. Аналогичные рассуждения приводят к тому, что ψ(0) = 0 и ψ(l) = 0. Таким образом мы определили граничные значения волновой ψ-функции.
. Частицу нельзя обнаружить с координатой x ≤ 0 и x ≥ l. Аналогичные рассуждения приводят к тому, что ψ(0) = 0 и ψ(l) = 0. Таким образом мы определили граничные значения волновой ψ-функции.
Пусть теперь 0 < x< l, где U(x) = 0. Тогда уравнение Шредингера примет вид:
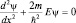 или
или 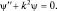
Решения такого уравнения нам уже известны: 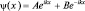 (общее решение, как суперпозиция частных). Применим граничные условия ψ(x) = 0 при x = 0. Тогда A + B = 0, то есть A = –B, а значит
(общее решение, как суперпозиция частных). Применим граничные условия ψ(x) = 0 при x = 0. Тогда A + B = 0, то есть A = –B, а значит 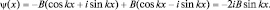 При x = l, ψ(l) = 0, т.е.
При x = l, ψ(l) = 0, т.е.  . Это возможно, если B = 0 (в этом случае при всех x ψ(x) = 0 и частица просто не существует в пространстве) или sin kl = 0, что возможно при kl = nπ, то есть
. Это возможно, если B = 0 (в этом случае при всех x ψ(x) = 0 и частица просто не существует в пространстве) или sin kl = 0, что возможно при kl = nπ, то есть 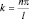 . Вычислим энергию:
. Вычислим энергию:
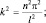
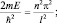
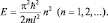 (1.6.2)
(1.6.2)
Величина энергии оказалась «квантованной». Теперь вернемся к ψ-функции и вычислим константу В из условия нормировки: 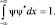 Тогда имеем:
Тогда имеем:
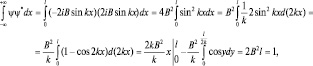
откуда 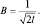
Окончательный вид решения можно записать следующим образом:
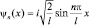 ,
,
а функция плотности вероятности равна 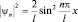 .
.
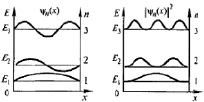
Рис. 10. Стационарные состояния микрообъекта в «потенциальном ящике»
Изобразим полученное решение графически (рис. 10). Большие квантовые числа приводят к тому, что функция плотности вероятности оказывается постоянной, что характерно для движения шарика между двумя упругими стенками (принцип соответствия).
