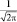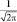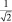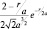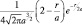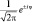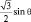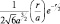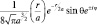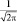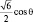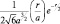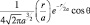Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

СТАТИСТИЧЕСКИЕ МОДЕЛИ В КВАНТОВОЙ ФИЗИКЕ ЭКОЛОГИИ И ЭКОНОМИКЕ

Рау В. Г., Рау Т. Ф., Малеев А. В.,

§ 1.8. Квантовомеханические модели. Атом водорода

Движение электрона в водородоподобном атоме происходит в центральном, сферически-симметричном поле кулоновских сил, поэтому для выяснения поведения электрона следует выбрать в центре ядра начало сферической системы координат. Тогда, исследуя стационарное движение микрообъекта, необходимо запивать и решить стационарное уравнение Шредингера:

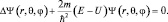(1.8.1)

Вид оператора Лапласа в этой системе координат записывается следующим образом:

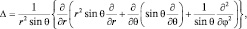
а потенциальная энергия: 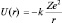. Уравнение Шредингера примет вид:

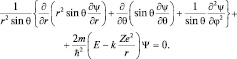(1.8.2)

Для решения уравнения воспользуемся методом разделения переменных, предложенным Ш. Фурье. Решение ищется в виде произведения трех функций, каждая из которых зависит лишь от одной переменной, т.е. 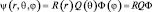. Тогда уравнение примет вид:

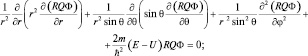
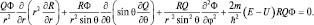
После умножения на 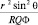, имеем:

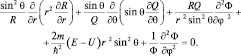
Перенося направо все члены, зависящие от переменной φ, получим: 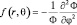, что возможно, если обе части уравнения равны одной и той же постоянной, которую обозначим 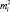. Тогда для левой части имеем:

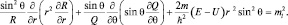
После деления на sin2θ и разделения переменных, получим: v(r) = w(θ), что возможно, если v(r) = w(θ) = const. Обозначая константу l(l + 1), окончательно имеем «триаду» уравнений:

1)

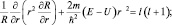
2)

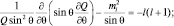
3) 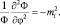(1.8.3)

Третье уравнение выглядит наиболее просто и имеет решение: 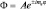, где φ – циклическая координата. Тогда однозначность решения требует, чтобы Φ(φ) = Φ(φ + 2π), а поэтому или 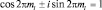, откуда следует, что cos 2πml = 1, что возможно, когда ml принимает целочисленные значения. Из условия нормировки легко вычислить величину A:

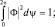
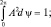
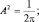
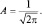
Это, в свою очередь, позволяет получить проекцию Lz вектора момента импульса. Действительно, для оператора 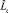справедливо выражение: 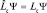, но 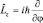а тогда 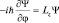. Если Ψ = RQΦ, то 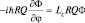, a 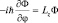. Зная вид функции, получим:

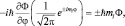
т.е. .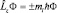

Собственные значения (измеряемая величина) проекции импульса равны Lz = mlħ, где ml может принимать как положительные, так и отрицательные значения. Таким образом, проекция момента импульса квантована и кратна постоянной Планка ħ.

Из второго уравнения «триады» удается рассчитать модуль вектора момента импульса: Если вместо 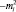записать 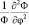. (из третьего уравнения) и умножить обе части на –ħ2RΦ, то получим следующее равенство:

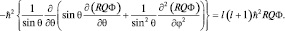(1.8.4)

Если обратится к «списку» операторов квантовой механики, то можно обнаружить, что слева стоит оператор момента импульса в квадрате, примененный к Ψ-функции, т.е. записано следующее равенство:

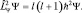
Это означает, что собственным значением квадрата модуля вектора момента является величина L2 = l(l + 1)ħ. Проекция момента, как мы уже знаем, квантована, что возможно только тогда, когда и сама величина вектора L квантована, откуда следует, что l принимает дискретный ряд значений. Так как проекция вектора не больше модуля самого вектора, тогда Lz ≤ L, 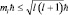, т.е. 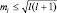, что при больших l (когда l >> 1) можно записать таким образом: ml ≤ l, то есть, ml изменяется пределах от –l до +l.

Теперь остановимся на решениях первого и второго уравнений. Сравним их вид с уравнением для квантовомеханического осциллятора.

Имея в виду, что оператор Лапласа равен Δ = Δx + Δy + Δz в декартовой, а Δ = Δr + Δθ + Δφ – в сферической системе координат, первое уравнение примет вид: ΔrR + f(r)R = 0, второе уравнение также запишется в виде: ΔθQ + f(sin θ)Q = 0, а для осциллятора ранее имели: ΔxΨ + f(x)Ψ = 0. Решение последнего уравнения определилось полиномом Эрмита, поэтому можно сразу сказать, что и первое, и второе уравнения имеют в качестве решений полиномы, и характеризуются квантованием. Для того, чтобы не повторять многократно один и тот же математический прием, не содержащий новых физических идей, выпишем лишь результаты решений. Для первого уравнения

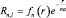
где 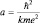(радиус первой «боровской» орбиты), а fn(r) – полиномы Лагерра; 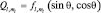характеризует полином Лежандра. Значение первых членов полиномов приводится в справочной литературе, поэтому нам остается лишь выписать хотя бы некоторые из них. Окончательно имеем: 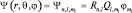, т.е. состояние определяется тремя квантовыми числами: n, ml, l или в порядке их важности n, l, ml. Аналогично тому, как l ограничивает значение ml, главное квантовое число n ограничивает l. Так как, то l изменяется в приделах от 0 до lmax = n – 1.

Для решения конкретных задач нам понадобится следующая табл. 3.

Таблица 3

Состояние электрона в атоме водорода

В первое уравнение входит величина полной энергии. Вычислим ее для первого состояния, т.е. при l = 0, n = nr = 1, 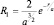, используя уравнение Шредингера:

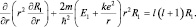
Найдем производную

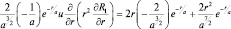
и подставим результат в первое уравнение:

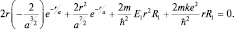
Если ввести радиус первой «боровской» орбиты а в атоме водорода, то получим следующее:

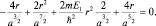
После преобразования имеем: 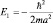или 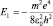, что совпадает со значением энергии в первом квантовом состоянии атома водорода в теории Бора. Аналогичное решение для состояния Ψn00 позволяет записать: 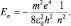Если l ≠ 0, то n = nr + l + 1 (без вывода). Итак, все основные физические величины, характеризующие атом водорода, найдены:

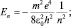
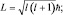Lz = mlħ. (1.8.5)

Выясним характер движения электрона в состояниях Ψ100, Ψ200 и Ψ210. При этом имеет смысл говорить лишь о плотности вероятности его появления в той или иной точке пространства. По определению функции плотности вероятности можно записать 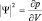, где ∂p – вероятность обнаружения электрона в малом объеме ∂V. В сферической системе координат, считая полный объем атома объемом шара, т.е. 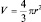, имеем: 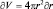, а тогда

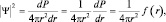
где f(r) характеризует вероятность появления электрона в единичном интервале r – координаты. Эту функцию уже можно «изобразить» в пространстве:

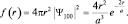
Экстремальные точки функции f(r) найдем из условия f′(r) = 0:

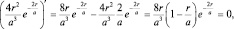
что возможно при r1 = O(min); r2 = a(max); r3 = ∞(min).

Для состояния Ψ100 график плотности вероятности f(r) имеет вид, изображенный на рис. 13. Но вот состояние Ψ211 уже не удается представить так просто, поскольку появляется зависимость этой функции от угла θ:

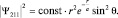
Сферически симметричный слой плотности вероятности f(r) «моделируется» функцией sin2θ, которая при θ = 0 обращается в 0, а при θ = 90° максимальна. То, что остается после умножения, имеет в сечении вид «гантели» (см. рис. 14). Конечно, плотность вероятности убывает до нуля лишь на бесконечности, но основная

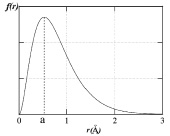
Рис. 13. График функции f100(r) «плотность» сосредоточена вблизи ядра

Для состояния 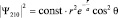имеем: («гантель» расположена вдоль оси Oz, где угол θ = 0 и cos2θ = 1.

Энергия электрона в рассмотренных состояниях атома водорода Н (в отсутствии внешних полей) одинакова. Говорят в этом случае о «вырождении» энергии. Сопоставляя полученные сведения с теорией атома водорода (по Бору), необходимо сделать вывод о том, что на самом деле в различных состояниях не следует говорить об орбитах в движении электрона – это было запрещено уже соотношением неопределенностей. Можно оставить это понятие только как приближение к истине: орбита – это геометрическое место точек, вблизи которых электрон бывает наиболее часто. Движение электрона «хаотично» и может быть описано только в терминах теории вероятностей. Различные состояния электронной плотности представлены на рисунке. Кроме этого, показано образование химической (ковалентной) связи, которая осуществляется при наложении электронных плотностей отдельных атомных орбиталей, которые могут характеризоваться различными квантовыми числами. С точки зрения теории, молекулярная орбиталь является линейной комбинацией атомных орбиталей.

Рис. 14. Распределение электронной плотности в атоме Н и молекуле Н2

Диаграмма энергетических уровней атома водорода с различными квантовыми числами, а так же спектральные серии в излучении представлены на следующем рисунке (рис. 15).

При главном квантовом числе n = 1, 2, 3, … вводится символьное обозначение для каждой «оболочки»: K, L, M, N,….Обозначения состояний с различными орбитальными квантовыми числами l (орбиталями) понятны из диаграммы.

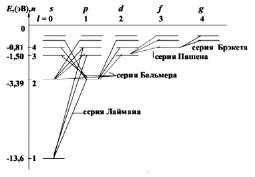
Рис. 15. Энергетические уровни в атоме водорода

Выводы:

1. Состояние электрона в атоме квантовано.

2. Энергия принимает дискретный ряд стационарных значений.

3. Движение электрона «хаотично», на наиболее часто он бывает на расстояниях, близких к «боровской орбите».

4. Введем плотность заряда ρ. Тогда

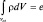и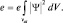

Плотность заряда и плотность вероятности связаны: 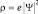(ρ – «электронная плотность»). Распределение электронной плотности в пространстве определяется состоянием атома или молекулы, то есть зависит от набора квантовых чисел.