Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

СТАТИСТИЧЕСКИЕ МОДЕЛИ В КВАНТОВОЙ ФИЗИКЕ ЭКОЛОГИИ И ЭКОНОМИКЕ

Рау В. Г., Рау Т. Ф., Малеев А. В.,

§ 1.9. Модель многоэлектронного атома. Эффект Зеемана. Спин электрона

Сложные атомы отличаются от атома водорода, прежде всего тем, что кроме взаимодействия электрона с ядром появляется межэлектронное взаимодействие, а тогда

,

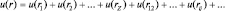где rij – расстояние между электронами в атоме. Если взаимодействие между электронами было бы сильнее, чем у электронов с ядром, то атомная система не смогла бы существовать из-за отталкивания электронов.

Поэтому, пренебрегая величинами u(rij), можно ввести задачу к анализу движения электрона в эффективном поле ядра (заряд которого уменьшен на величину заряда электронов, не включая исходного, как правило, внешнего, наиболее удаленного от ядра).

В этом случае удается решить уравнение Шредингера и получить приближенный ответ, аналогичный решению для одного электрона в водородоподобном атоме (ионе). Зная характер движения электрона в различных состояниях, можно рассчитать и то воздействие, которое окажет электрон на атомный «остов», т.е. узнать, как этот «остов» деформируется.

Повторяя решение многократно, в принципе, возможно проанализировать поведение электрона все с большей и большей точностью. Однако, начиная с какого-то момента эти поправки к энергии электрона станут соизмеримыми с энергией взаимодействия отдельных электронов и дальнейшая процедура расчета значительно усложняется, более сложными будут задачи о состоянии электронов в молекулах – многоядерных системах. Здесь мало помогает даже такое «одноэлектронное» приближение. Тем не менее, для качественного анализа можно считать электроны независимыми и сверять расчеты с экспериментальными исследованиями, открывая новые свойства атомов эмпирически.

Одной из важнейших проблем, не разрешенных классической физикой, оставалось объяснение магнитных свойств вещества, поэтому обсуждение поведения атомов в магнитном поле с соответствующей экспериментальной проверкой оказалось актуальным, полезным для различных технологий. Считая, что в некоторых состояниях электронная плотность атома имеет в среднем вид «кольца», можно анализировать взаимодействие атома c внешним полем, как взаимодействие кругового тока 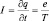(где Т – период «обращения» электрона) с магнитным полем, характеризующимся вектором магнитной индукции 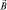(рис. 16).

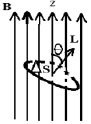
Рис. 16. Атом в магнитном поле

Из электродинамики известна величина энергии взаимодействия кругового тока с внешним магнитным полем, поток вектора которого через площадку ΔS равен ΔΦ: 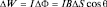, но IΔS есть величина магнитного момента кругового тока, а поэтому 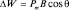. Гиромагнитное отношение для кругового тока нам известно:

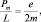
а .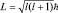

Тогда

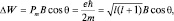
но 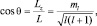поэтому 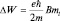, или, обозначая 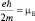(магнетон Бора), имеем: .

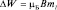Так как, например, при l = 1, ml = –1, 0, +1, к энергетическому уровню 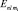добавляется (или вычитается) энергия ΔW и он «расщепится» на три подуровня (рис. 17). В соответствующем спектре атома, помещенного в магнитное поле, должны появиться дополнительные «спектральные» линии. Этот эффект впервые наблюдал Зееман и поэтому носит название «нормального эффекта Зеемана». Кстати, становится ясным наименование квантового числа ml, названного магнитным орбитальным квантовым числом, так как именно оно характеризует энергию взаимодействия «орбитального» движения электрона в атоме с внешним магнитным полем. Без внешнего поля этот уровень трижды «вырожден», так как ΔW = 0. Но в сложных атомах вырождение снимается и без внешнего поля, о причине которого легко догадаться, так как всегда имеются поля, создаваемы другими электронами.

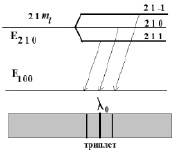
Рис. 17. «Расщепление» спектральных линий (эффект Зеемана)

Из факта взаимодействия атома с магнитным полем следует сразу несколько выводов. Если наблюдается взаимодействие электрона с внешними по отношению к нему полями, то энергетические уровни смещаются. Это приводит к тому, что в спектре сложного атома длины волн при переходах с уровней En10 и En00 оказываются различными. Дополнительное воздействие внутри атома на внешний (как правило) электрон оказывают остальные электроны. Справедливо и обратное утверждение: если в спектре наблюдается эффект «расщепления» линий («тонкая структура» спектральных линий»), то это означает, что у электрона появилось какое-то дополнительное взаимодействие с внешними полями и дополнительно «движение», кроме орбитального.

По своему строению ближе всего к водородоподобным атомам относятся щелочные металлы, у которых внешний электрон «легко» отщепляется с образованием иона. Это означает, что один электрон у металла находится далеко от ядра, а поэтому весь атом можно представить как электрон плюс положительный остаток – «остов», имеющий заряд q = e+. Этот внешний электрон занимает в атоме «энергетические ступеньки», расположенные аналогично уровням в водородоподобном атоме. При «переходах» между уровнями атомы излучают в видимом (оптическом) диапазоне длин волн» а поэтому такой внешний электрон часто называют «оптическим». Уравнение Шредингера в этом случае по форме не отличается от его записи для водородоподобных атомов, однако потенциальная энергия взаимодействия валентного оптического электрона с остовом атома щелочного металла должна быть представлена в виде разложения на составляющие его взаимодействия с точечным зарядом, диполем, квадруполем и т.д., как это делается в электродинамике при расчетах полей сложно распределенных зарядов. Математически такой подход соответствует разложению функции u(r) в ряд (1.9.1):

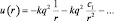(1.9.1)

На больших расстояниях взаимодействие ослабевает, поэтому можно ограничиться двумя первыми слагаемыми в (1.9.1). Тогда:

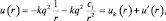
где величина uk(r) – аналогична записи потенциальной энергии взаимодействия, в атоме водорода, а U′(r) характеризует дополнительное взаимодействие электрона с атомным остовом щелочного металла.

При решении уравнения Шредингера методом Фурье изменится лишь запись «радиального» уравнения в системе (8.3), которое примет вид (1.9.2):

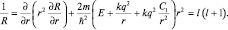(1.9.2)

Преобразуем это уравнение следующим образом:

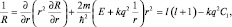
которое формально аналогично основному уравнению, если ввести обозначение 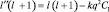. Считая величину, l′ как и l положительной и решая квадратное уравнение относительно, l′ имеем:

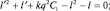
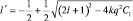
или

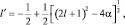
где α = kq2C1.

Из разложения (a + b)n в биномиальный ряд, полагая a = (2l + 1)2 и b = –4α, а также ограничиваясь первыми членами ряда, получим:

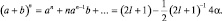
Тогда 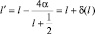. Энергия n-го состояния электрона щелочного металла запишется как 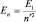, где n′ = nr + l′ + 1. Тогда

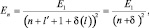(1.9.3)

если иметь в виду, что n = nr + l + 1.

Поправка δ объясняет смещение спектральных линий соответствующих уровней щелочного металла по сравнению с атомом водорода.

При помещении атома щелочного металла во внешнее магнитное поле каждый подуровень расщепляется на мультиплеты в соответствии с эффектом Зеемана. Но кроме этого, в спектре щелочных металлов было замечено такое двойное («дублетное») расщепление линий, которое не могло быть описано с помощью магнитного орбитального квантового числа, так как, во-первых, величина расщепления, т.е. расходимость линий в спектре была меньше, чем у триплетов и мультиплетов, а во-вторых, средней линии при этом не наблюдалось. Эти отличия позволяли предположить, что причина не кроется в «орбитальном» движении электрона, а может быть связана с дополнительным «собственным» движением, аналогичным (в планетарной модели) вращению планет вокруг собственной оси. Именно такую мысль впервые высказали Уленбек и Гаудсмит, назвав величину механического момента собственного движения спином («спин» – веретено»). Также как все характеристики движения в атоме кантованы, эта величина должна быть квантована и, чтобы достичь согласия с экспериментом, добавочная энергия взаимодействия с магнитным полем должна всегда принимать всего два значения. Соответствующее квантовое число также принимает два значения в отличие от ml, количество значений которых может быть только нечетным.

Сравним энергии: ΔW = μБBml и ΔWсоб = μБBms, где величина ms, принимающая эти 2 возможных значения по аналогии с ml, была названа магнитным спиновым квантовым числом. Вдвое меньшая расходимость линий в спектре «подсказывает», что 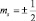. Если обозначить собственный механический момент электрона , а его проекцию на ось Oz как Sz, то по аналогии с орбитальным моментом 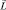, следует записать: если Lz = mlħ, то

Sz = msħ, (1.9.4)

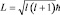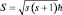если , то , где 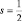есть спиновое квантовое число.

Таким образом, электрон обладает не только массой и зарядом, но и собственным механическим моментом. Законы электродинамики и механики требуют, чтобы у заряженной частицы, обладающей механическим моментом, был магнитный момент. Для «орбитального» движения гиромагнитное отношение 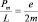позволяет записать что 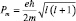, а в случае «собственного» движения 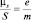, так как существует эксперименты (опыты Эйнштейна – де Гааэа и Барнета) с магнитными материалами, приводящие именно к данному результату. Тогда 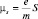или .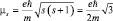

Проекция магнитного момент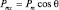а , а 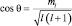и тогда 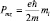. Аналогично рассуждая, имеем:

; .

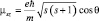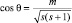Окончательно получим:

.

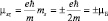Если у свободного электрона ось совместить со спином, то его магнитной характеристикой явится величина магнетона Бора, которая равна:

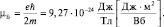
Эта величина, конечно, мала, но учитывая количество электронов в веществе и ограниченные возможности в ориентации («по полю или против поля») следует признать, что магнитные свойства многих веществ могут определяться в основном собственными магнитными моментами электронов.

Возникает необходимость прямой проверки наличия у электрона собственного магнитного и механического моментов. На том пути у экспериментатора возникает ряд трудностей. Первая трудность: как «приготовить» электроны; вторая – каким должно бить магнитное поле?; третья – как «отделить электроны с 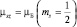от электронов 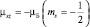, т.е. ориентированных по «полю» или «против поля»?

Допустим, что мы приготовили пучок электронов в электроннолучевой трубке и поместили этот пучок во внешнее магнитное поле. Тогда модельно, можно предсказать результат взаимодействия» рассматривая пучок электронов как направленно движущиеся «магнитные стрелки» (механическая аналогия). В поле с индукцией 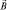эти стрелки ориентируются по двум направлениям.

Если поле 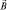однородно, то силы и 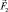, действующие на электроны, одинаковы по величине и направлены в различные стороны, компенсируя друг друга. На экране все электроны попадут в одну и ту же точку, т.е. разделения пучка не произойдет. Если же сделать поле неоднородным, то и 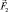станут различными и эта разница будет тем более значительной, чем крупнее размер «магнитной стрелки». Другими словами, размеры объекта должны быть соизмеримы с неоднородностям магнитного поля. Размеры электрона настолько малы, что практически не удается провести задуманный эксперимент и необходимо в качестве «магнитной стрелки» избрать более крупную систему – атом. При этом состояние атома должно быть таким, чтобы его магнитные свойства определялись магнитным моментом только одного электрона. Может ли это быть достигнуто в многоэлектрон- ной системе?

Чтобы ответить на этот вопрос, рассмотрим атомы с точки зрения совокупности векторов-моментов как орбитальных, так и собственных. Рассмотрим понятие о «векторной модели» атома.

Уже в механике системы точек формулировалась теорема о том, что момент импульса системы равен сумме моментов импульса составляющих его частей (точек) Обозначая полный механический момент атома 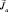, мы должны, следовательно, записать:

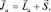(1.9.5)

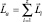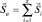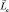где , , а – суммарный механический момент орбитального движения электронов (Z – порядковый номер элемента); а 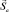– суммарный механический момент собственного движения тех же электронов. Отличие от механической системы заключится в том, что теперь каждая из стих величин квантована:

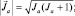
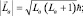
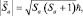(1.9.6)

где индекс «a» говорит о том, что мы имеем дело с атомом. Можно ввести и величину полного момента импульса по отношению к отдельному электрону. Тогда

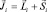
где 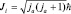; ; 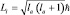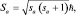(1.9.7)

где j – квантовое число полного момента электрона. В конечном счете, результат сложения зависит от положения всех 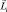и 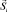в пространстве, что определяется квантованием проекций или квантовыми числами ml и ms. Понятно, что вектор 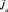имеет смысл ориентировать относительно поля 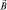, но как быть с остальными векторами? И здесь важным оказывается факт взаимодействия. Действительно, почему вектор момента 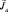ориентируется во внешнем поле? По-видимому, потому, что с ним связан магнитный момент 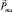, и это приводит к ориентации и механического момента вместе с магнитным, т.е. атом также следует изобразить в виде «магнитной стрелки», только более крупной, чем электрон. А вот спиновый момент 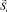может ориентироваться и относительно 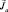и относительно 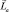и 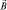в зависимости от того, какое поле сильнее. В этом случае можно говорить, например, «спин – орбитальном взаимодействии». В эту схему начинают «включаться» электростатические взаимодействия.

Для атомов легких элементов наибольшее взаимодействие – это спин – орбитальное, а для тяжелых – существенно взаимодействие спинового и орбитального с полным моментом атома. Таким образом «формируется» состояние атома. Так, например, если символ состояния обозначается 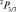, то это означает, что La = 1, 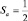(число 2 = Sa + 1 именуют кратностью состояния), 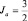, так как Ja = La + Sa. Исторически эти обозначения называют символами термов. Буквами S, P, D, F и т.д. обозначают состояния соответственно для 0, 1, 2, 3 и т.д. Такие же буквы характеризуют и отдельный электрон. Если орбитальное квантовое число l = 1, 2, 3, ..., то соответствующие буквы s, p, d, f обозначают эти состояния. Для электронов в состоянии с главным квантовым числом n = 1, 2, 3, 4, ... приняты обозначения латинскими заглавными буквами К, L, М, N, O, ... В этом случае говорят, что электроны находятся на К-слое, L-слое, М-слое и т.д., а затем на 1s-оболочке, 2р-оболочке и т.п.

Рассмотрим поведение веществ во внешнем магнитном поле и магнитные свойства вещества.

1. Если 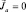, магнитный момент 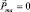, то вещество, состоящее из таких атомов «равнодушно» ко внешнему полю, т.е. оно является диамагнетиком. Правда, внешнее поле «деформируем» орбитальное движение электронов и «наводит», индуцирует в атоме дополнительные движения, на которые расходуется энергия внешнего поля. Поэтому диамагнитный эффект ослабления магнитного поля наблюдается для всех веществ. Если внешнее поле 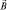переменное во времени 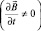, то диамагнетизм можно описать качественно в рамках явлений электромагнитной индукции классической электродинамики. Возникают эффекты «выталкивания» диамагнетика из поля в моменты «включения» поля и «втягивании» в момент «выключения».

2. Если 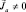, то во внешнем поле 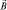происходит ориентация 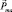, и поля атомов складываются с внешнем полем, усиливая его. Тепловое движение «мешает» такой ориентации, поэтому, во-первых, результирующее поле пропорционально внешнему полю, а во-вторых, при отключении внешнего поля вещество «само размагничивается».

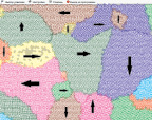
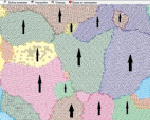
3. Наконец, для понимания «магнетизма» необходимо упомянуть о «спиновом» магнетизме или, точнее, о ферромагнетизме. Для ферромагнетиков 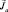, в основном обеспечивается спиновыми составляющими, которые в монокристаллических блоках («доменах») ориентированы параллельно. Вещество («магнитная руда»), составленное из доменов, может быть модельно представлено (рис. 18). На рис. 18а домены не ориентированы, а на рис. 18б – ориентированы по внешнему полю.

а б

Рис. 18. Доменная структура ферромагнетиков

В отсутствии внешнего поля отдельные домены могут иметь различные направления суммарного магнитного момента, входящих в него атомов. При наличии внешнего поля происходит резкий поворот магнитных моментов «по полю В0» («скачки Баркгаузена»), что приводит к значительному усилению поля за счет магнитного поля доменов. Трение между доменами мешает их разориентации (при выключении поля) тепловым движением, поэтому для ферромагнетиков наблюдается явление остаточного магнетизма, что может быть использовано для практически; (радиотехника, электротехника, приборостроение, автоматика и т.п.).

Доказательством существования спина явились опыты Штерна и Герлаха. Для выявления существования спинового момента атомы могут быть представлены магнитными стрелками. Расчет, проведенный для атомов серебра, показал, что суммарный момент при учете всех электронов равен нулю, кроме внешнего электрона, у которого спин не равен нулю (не скомпенсирован). Поэтому магнитные свойства атомов серебра полностью определяются только спином, (а значит собственным магнитным моментом внешнего электрона), если таковой действительно существует. При наличии спинового момента его вектор ориентирован либо по полю, либо против поля. Создав неоднородное магнитное поле, Штерн и Герлах обнаружили на экране две полоски осажденных атомов серебра, пропущенных через внешнее магнитное поле, доказав тем самым не только существование магнитного момента у электронов, но и его квантованность с квантовым числом, принимающим два и только два возможных значения. Попытка трактовать образование спина как результат собственного механического вращения электрона тем не менее окончилась неудачей: чтобы магнитный момент электрона был равен магнетону Бора необходимо, чтобы скорость движения отдельных частей самого электрона была больше с – скорости света в вакууме.