Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

СТАТИСТИЧЕСКИЕ МОДЕЛИ В КВАНТОВОЙ ФИЗИКЕ ЭКОЛОГИИ И ЭКОНОМИКЕ

Рау В. Г., Рау Т. Ф., Малеев А. В.,

§ 1.11. Квантовомеханические модели. Туннельный эффект

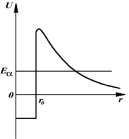
Потенциальную кривую α-частицы и ядра, изображенную раньше преобразуем так, чтобы было удобнее вычислять, не меняя существа задачи (Umax > Eα). Находясь в ядре, α-частица «зажата стенками «ящика» U(r).

а б

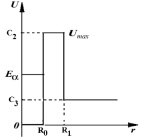
Рис. 22. Модель потенциальной ямы в ядре

Задачу на стационарное движение α-частицы разбиваем на три части по областям, так как это изображено на рис. 22. При решении этой задачи возможны два варианта: первый, когда полная энергия α-частицы E > Umax = C2, и второй, когда E < Umax. В уравнении Шредингера для первого случая (кинетическая энергия E – U =T > 0) имеем: 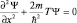или Ψ″ + k2Ψ = 0. Решением уравнения является функция Ψ = Ψ0e±ikx (стационарная «волна»), где величина k фиксирует длину волны де-Бройля для каждой области: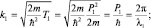 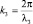и при этом λ3 > λ1. Всюду, во всем пространстве существует вероятность обнаружения α-частицы, отличная от нуля (кроме, разумеется, бесконечно удаленных точек). Ядро не в состоянии «удержать» α-частицу, но на границах областей, а значит и на отрезках (OR0) и (R0R1) оси возможно обратное движение («отраженные волны»).

Для области II (при E < Umax) уравнение Шредингера 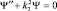, где 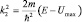, имеет решение в виде: 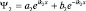. Так как теперь E < Umax, а значит 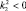, то подставив 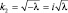в решение, получим: 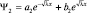. При x → ∞ второе слагаемое неограниченно возрастает и чтобы решение не было бесконечным, положим b2 = 0. Тогда 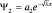, что графически изображено в области II экспоненциально убывающей кривой, «спад» которой зависит от разности (Umax – E). Очевидно, стабильные ядра характеризуются большим значением этой разности, что приводит к 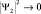при возрастающих величинах x уже внутри потенциального барьера. Для радиоактивных элементов величина Umax – E невелика, поэтому плотность вероятности медленно убывает при x → R1. Вероятность обнаружения α-частицы вне ядра (за пределами барьера) в этом случае существенно велика.

Решение уравнения Шредингера для третьей области аналогично решению для первой, но с другим значением 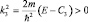. Теперь осталось только найти характеристику проницаемости барьера, его своеобразной «прозрачное и». Естественно предположить, что если входящая в область волна и выходящая из нее одинаковы, то прозрачность барьера стопроцентная, если же волна «затухает», то величина отношения волн, входящих к выходящим, и будет служить мерой проницаемости. Но, как мы уже говорили раньше, измеряемой характеристикой волны является квадрат ее модуля, а поэтому определим прозрачность барьера окончательно в виде отношения: 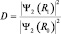. Вычисления (без учета отражений от стенок барьера) приводят к следующему результату:

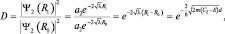(1.11.1)

где d = R1 – R0 ширина барьера.

Если форма барьера не прямоугольная, а характеризуется функцией U(x), то величина прозрачности D может быть рассчитана интегрированием по малым «сечениям» ширины барьера. Окончательно имеем:

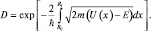
Туннельный эффект был изучен теоретически Г. Гамовым в 1928 году. В 1982 году Г. Биннигом и Х. Рёрером был создан сканирующий туннельный микроскоп (СТМ), который открыл очень большие возможности научных и прикладных исследований в области наноструктурного анализа и явился первым техническим устройством, с помощью которого была осуществлена наглядная визуализация атомов и молекул (выше (рис. 23) представлена принципиальная схема туннельного микроскопа).

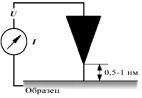
Рис. 23. Принцип работы туннельного микроскопа

Принцип работы СТМ заключается в следующем: к поверхности проводящего образца на характерное межатомное расстояние, составляющее доли нанометра, подводится очень тонкое металлическое острие (игла). При приложении между образцом и иглой разности потенциалов U ~ 0,1–1 В в цепи появляется ток, обусловленный туннелированием электронов через зазор между ними. Ток составляет величину около 10 нА.

В заключение раздела «Квантовая механика» рассмотрим задачу о происхождении спектральных линий, то есть выясним, каким образом квантовая механика позволяет получить результаты спектрального анализа.

Напомню, что линейчатые спектры атома водорода (по Бору) возникали при переходе атома из одного состояния в другое: получим этот же результат исходя только из основных положений квантовой механики.

Во-первых, существуют функции состояния электрона в атоме:

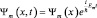и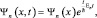

а во-вторых, существует состояние, определяемое как их суперпозиция:

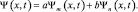
Если среднее значение координаты электрона в сложном состоянии окажется зависящим от времени периодически, то это будет означать, что электрон излучает. В противном случае электрон излучать электромагнитную волну не должен. Найдем .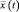

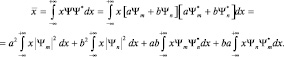
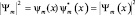
не зависит от времени (т.е., находясь в m-состоянии электрон не излучает. Это же относится к стационарному состоянию 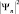, а величина 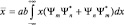от времени зависит. Действительно, считая, что произведения 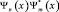и 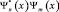одинаковы, т.к. функции Ψn(x) и 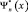равноправны, имеем:

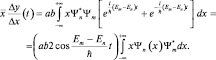
(В расчетах использована формула: 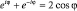). Значение самого интеграла от времени не зависит, поэтому окончательно можно написать: 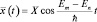или 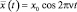. Частота изменения среднего значения координат (частота «осцилляции») отсюда равна:

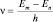или hν = Em – En, (1.11.2)

что совпадает с теорией Бора.