
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
§ 2.4. Распределение молекул идеального газа по величине скорости и по энергии
Как отмечалось выше, пространство скоростей изотропно, поэтому поиск распределения вероятностей по величине (модулю) скорости следует вести в сферически симметричном пространстве. Выберем в однородном пространстве проекций скоростей произвольную точку и выделим все радиус-векторы скорости 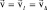 , идущие от выбранной точки по всем направлениям li. Концы векторов попадут вследствие изотропности на поверхность сферы. Изотропность пространства скоростей позволяет также записать, что плотность вероятности в точках пространства скоростей одинакова для всех точек, расположенных от выбранной точки на расстоянии v = vli: f(v) = f(vli) = f(vl).
, идущие от выбранной точки по всем направлениям li. Концы векторов попадут вследствие изотропности на поверхность сферы. Изотропность пространства скоростей позволяет также записать, что плотность вероятности в точках пространства скоростей одинакова для всех точек, расположенных от выбранной точки на расстоянии v = vli: f(v) = f(vli) = f(vl).
Тогда
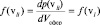 ,
,
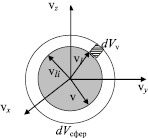
Рис. 30. Шаровой слой сферического пространства скоростей
где величина dVсфер определяет размер элементарного объема шарового сферического слоя в пространстве скоростей (рис. 30), который можно выразить через величину скорости:
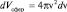 .
.
Определим плотность вероятности как вероятность обнаружения у произвольно выбранной молекулы величины скорости, попадающей в единичный интервал скоростей: 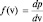 и вычислим эту плотность, используя два последних равенства:
и вычислим эту плотность, используя два последних равенства:
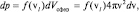
откуда имеем:
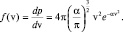 (2.4.1)
(2.4.1)
Функцию (1.4.1) называют распределением Максвелла по величине скорости. На рис. 31 показан график функции распределения по скоростям. Параметрами этого распределения, кроме константы α, являются скорости: наиболее вероятная – vi, средняя –  и среднеквадратичная –
и среднеквадратичная – 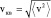 .
.
Получить величину наиболее вероятной скорости несложно, взяв производную от функции распределения и приравняв ее к нулю (условие максимума). Для вычисления двух других скоростей нужно воспользоваться расчетом среднего и среднеквадратичного значения случайной величины x из теории вероятностей:
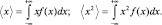 (2.4.2)
(2.4.2)
При расчете определенных интегралов вида (1.4.2) и решения задач используем справочные данные:
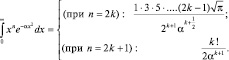 (2.4.3)
(2.4.3)
Расчет наиболее вероятной и средних скоростей молекул газа дает следующие величины:
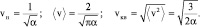 (2.4.4)
(2.4.4)
Из определения температуры, как меры средней кинетической энергии молекул газа, легко выяснить физический смысл параметра α, используя последнее равенство в (2.4.4) и следствие основного уравнения МКТ:
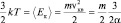 .
.
Отсюда следует: 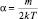 . Вид распределения Максвелла по скоростям будет выглядеть следующим образом:
. Вид распределения Максвелла по скоростям будет выглядеть следующим образом:
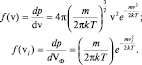 (2.4.5)
(2.4.5)
По отношению к газу «в целом» эта функция показывает, какова доля всех молекул газа обладает скоростями, попадающими в единичный интервал скоростей, то есть 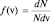 .
.
Для того чтобы убедиться в правильности использования в статистике следствия из основного уравнения МКТ, получим вначале распределение по энергии молекул идеального газа 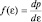 , где
, где 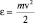 – энергия отдельной молекулы газа. Затем стандартной формулой (2.4.2) поиска среднего значения случайной величины, вычислим
– энергия отдельной молекулы газа. Затем стандартной формулой (2.4.2) поиска среднего значения случайной величины, вычислим 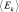 . Из распределения (2.4.5) и формулы для кинетической энергии отдельной молекулы следует:
. Из распределения (2.4.5) и формулы для кинетической энергии отдельной молекулы следует:
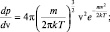
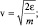
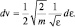
После подстановки величин v и dv в распределение по скоростям и простых преобразований получим распределение по энергиям:
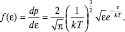 (2.4.5)
(2.4.5)
Графики распределения по энергиям при различных температурах представлены на рис. 32. Зная вид функции распределения можно вычислить среднюю энергию молекул идеального газа.
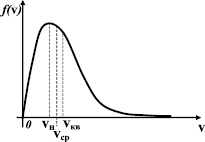
Рис. 31. Графики распределения по энергиям при различных температурах
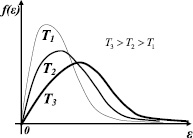
Рис. 32. Графики распределения по энергиям при различных температурах
Используя формулу расчета среднего значения (2.4.2), будем иметь:
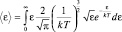 .
.
После замены переменных 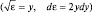 получим
получим
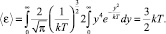
В идеальном газе, находящемся в сосуде, каждая молекула имеет три поступательных степени свободы, т.е. i = 3, поэтому полученный результат можно записать следующим образом: 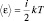 , где i – число степеней свободы одной молекулы. Этот факт является следствием теоремы о распределении энергии по степеням свободы: В состоянии термодинамического равновесия на одну степень свободы системы приходится энергия kT/2.
, где i – число степеней свободы одной молекулы. Этот факт является следствием теоремы о распределении энергии по степеням свободы: В состоянии термодинамического равновесия на одну степень свободы системы приходится энергия kT/2.
