Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
§ 3.2. Модель колебательных процессов в экономике
Оценка соотношения между количеством товара определенного вида и его ценой на рынке товаров во времени довольно часто оказываются коррелированными таким образом, что дефицит товара приводит к росту цены, а его излишек к падению цены. При этом, высокие цены влияют на производителя таким образом, что ему выгодно поставлять на рынок больше товаров для увеличения доходов, но это может привести к излишку товаров и новому падению цен. Таким образом, саморегуляция работы рынка, в определенном комплексе условий, происходит как бы автоматически (рис. 44).
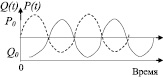
Рис. 44. Экспериментальные кривые изменения цены P и количества товара Q на рынке от времени
Рядовой покупатель обнаруживает при этом, что цены на товары имеют характер изменений во времени, но в то же время, приходя на рынок в «случайные моменты времени», он не может анализировать эти изменения детально. В лучшем случае, покупатель имеет набор случайных величин и даже может построить частотное распределение. Изобразим один из возможных вариантов гистограммы изменения цены, как случайной величины, равной отклонению от ее среднего значения.
Обозначим эту случайную величину отклонения цены на товар переменной, так же как и саму цену P. Тогда отклонение принимает как отрицательные, так и положительные значения.
Эта гистограмма (рис. 45.) легко аппроксимируется графиком функции Коши:
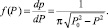
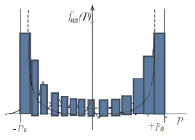
Рис. 45. Гистограмма распределения вероятностей для отклонения P
Вероятность наблюдения отклонения цены P за фиксируемый малый интервал времени dt приусловии, что существует полный интервал наблюдения T0, может быть записана по определению вероятности как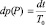 
. С другой стороны, исходя из определения функции плотности вероятности, имеем: dp(P) = f(P)dP. Поэтому справедливо следующее равенство:
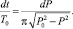
Так как переменные в этом уравнении уже разделены, то легко получить результат P(t) интегрированием левой и правой части. Правая часть содержит функцию, интеграл от которой дан в справочнике по математике. Тогда имеем:
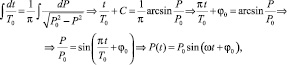
где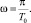 
Очевидно, что рассматриваемая модель процесса изменения цены на товар, функция плотности вероятности которой подчиняется распределению Коши, является динамической моделью периодического процесса. В экспериментах, связанных с построением гистограммы, самым важным для прогнозирования цены во времени, необходимо найти две характеристики процесса: период Т0 и начальную фазу φ0.
Если основными параметрами системы рынка считать цену товара P и скорость ее изменения, то в фазовом пространстве состояний системы для каждого момента времени можно ввести вектор состояния 
. Так как связь переменных со временем выражается через тригонометрические функции, то можно записать:
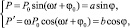
откуда следует (при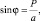 
):
.
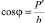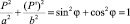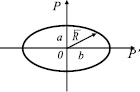
Рис. 46. Фазовая траектория процесса изменения случайной величины P и скорости ее изменения P′
На диаграмме состояний рынка, построенной в переменных P и P′, полученное уравнение будет представлять собой эллипс (рис. 46). Эта кривая второго порядка в данном случае называется фазовой траекторией и представляет собой еще одну модель рассматриваемого процесса. Так как основные переменные на фазовой траектории согласованы во времени, то процесс называется стационарным. Не изменяющимися характеристиками процесса являются полуоси эллипса, то есть величины P0 и P0ω, а также величина площади эллипса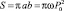 
. При нестационарном процессе (например, инфляционном росте цен) фазовая траектория будет представлять собой спираль.