
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
§ 3.3. Модель распределения вероятностей для посетителей рынка
Пусть большое количество посетителей рынка N, в момент его открытия хаотично двигаются по рыночной площади (рис. 47). Если известны размеры всей площади S, можно определить вероятность попадания ровно n-числа посетителей из N в произвольно выбранную торговую s-палатку (площадью s), находящуюся на территории рынка. Будем решать задачу при условии, что среди палаток нет предпочтительных по своим товарам и ценам. В этом случае все торговые точки являются равноправными. Так как движение людей хаотично, то их количество – n, посетившее выбранную палатку является случайной величиной, для которой можно найти распределение P(n).
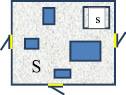
Рис. 47. Рыночная площадь
Мысленно пронумеруем всех посетителей и тогда вероятность попадания одного из них, выбранного под номером № 1 в палатку s будет равна 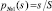 ; вероятность попадания двух первых по номеру людей в торговую точку (по теореме умножения вероятностей) будет равна
; вероятность попадания двух первых по номеру людей в торговую точку (по теореме умножения вероятностей) будет равна 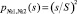 . Наконец, вероятность попадания от первого по номеру посетителя до n-го в выбранной палатке окажется равной
. Наконец, вероятность попадания от первого по номеру посетителя до n-го в выбранной палатке окажется равной 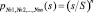 .
.
Остальные посетители не должны попасть в выбранную точку. Вероятность этого события по аналогии с предыдущими вариантами будет равна 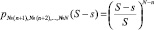 . Для того, чтобы только n первых по номеру посетителей попали в выбранную палатку, должны выполняться два последних события совместно с вероятностью, равной произведению вероятностей этих событий:
. Для того, чтобы только n первых по номеру посетителей попали в выбранную палатку, должны выполняться два последних события совместно с вероятностью, равной произведению вероятностей этих событий: 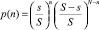 . Для расчета вероятности попадания любых n посетителей, а не только первых по номеру, в выбранную торговую точку, необходимо сложить вероятности p(n) столько раз, сколько существует вариантов выбора числа n – посетителей с неповторяющимися номерами из общего их количества N.
. Для расчета вероятности попадания любых n посетителей, а не только первых по номеру, в выбранную торговую точку, необходимо сложить вероятности p(n) столько раз, сколько существует вариантов выбора числа n – посетителей с неповторяющимися номерами из общего их количества N.
Из комбинаторики известно, что это число определяется сочетаниями из N по n. Тогда окончательно, так же, как это было сделано при выводе распределения молекул идеального газа по сосуду будем иметь:
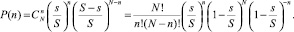
Для того, чтобы вести расчет только через количество посетителей рынка, введем параметр распределения m – как такое количество людей, которое пропорционально размеру выбранной палатки. Тогда всей площади рынка будет соответствовать полное число людей N и можно от отношения площадей перейти к отношению чисел посетителей: s/S = m/N. Полученное выше распределение можно упростить, считая, что, во-первых, N велико и, во-вторых, справедлива формула приближенного вычисления Стирлинга для N! ≈ (N/e)N (см. справочники по математике). Тогда получим для P(n) следующее выражение: 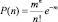 .
.
Полученная формула распределения, такая же как и для распределения молекул по сосуду, является математической моделью одной из систем рынка, и ее можно применять для решения задач.
