
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
1.2. Практическая реализация в среде имитационного моделирования
Исследуем пример моделирования СМО с отказами [2].
Требуется определить минимально необходимое число аварийно-спасательных судов на водохранилище. Критерием является обеспечение вероятности отказа не более 10 %.
Известно, что в сутки в среднем поступает ? = 2 вызова на оказание помощи. Поток заявок носит случайный характер и может быть описан законом Пуассона, а длительность обслуживания аппроксимируется показательным распределением. Таким образом коэффициенты вариации интервалов входящего потока заявок и интервалов обслуживания, соответственно, равны единице: ?? = ?m = 1.
Из статистических данных известно, что одно аварийно-спасательное судно может за сутки обслужить m = 4 заявки.
Решение.
Очевидно
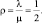
Если поставить на выполнение работ одно (n = 1) судно, то вероятность отказа в обслуживании:
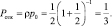
Очевидно, что 33 % отказов в обслуживании – слишком большая величина, поэтому проведем расчет для двух (n = 2) судов:
Вероятность простоя:
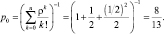
Вероятность отказа:
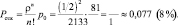
Относительная пропускная способность:
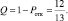
Абсолютная пропускная способность:
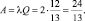
Среднее число занятых судов определяем по формуле:
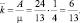
Среднее время пребывания заявки в СМО:
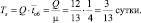
На рис. 1.2 приведена принципиальная схема рассматриваемой системы в среде имитационного моделирования AnyLogic [2].
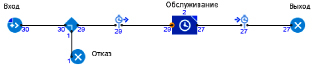
Рис. 1.2. Схема имитационной модели
Представленный фрагмент решения задачи свидетельствует о том, за определенный промежуток времени всего поступило 30 заявок на обслуживание, из которых одна получила отказ в те периоды, когда аварийно-спасательные суда были заняты.
На рис. 1.3 представлен временной график изменения количества аварийно-спасательных судов, задействованных в проведении спасательных мероприятий и гистограмма плотности вероятности распределения (с функцией распределения и средним значением) времени, затраченного на обслуживание.
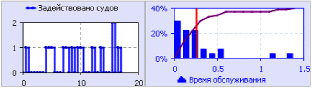
Рис. 1.3. Показатели функционирования СМО
