Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
2.2. Многоканальные СМО с ожиданием
Рассмотрим n-канальную (многоканальную) систему с неограниченной очередью. Поток заявок, поступающих в СМО, имеет интенсивность λ, а поток обслуживаний – интенсивность μ. На рис. 2.7 представлен граф состояний системы.

Рис. 2.7. Граф состояний для многоканальной СМО с неограниченной очередью
Система может находиться в одном из состояний:
S0 – в СМО заявок нет (все каналы свободны);
S1 – один канал занят, остальные свободны;
S2 – заняты два канала, остальные свободны;
…
Sk – занято k каналов, остальные свободны;
…
Sn – заняты все n каналов, (очереди нет);
Sn+1 – заняты все n каналов, одна заявка стоит в очереди;
…
Sn+r – заняты все n каналов, r заявок стоит в очереди;
…
Можно показать, что при 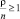 очередь будет расти до бесконечности, иначе справедливы формулы (например, [1]), представленные в табл. 3.
очередь будет расти до бесконечности, иначе справедливы формулы (например, [1]), представленные в табл. 3.
Таблица 3
Показатели работы СМО с неограниченной очередью
|
№ п/п |
Наименование |
Формула |
|
|
1 |
p0 |
Вероятность того, что система находится в состоянии S0 |
|
|
2 |
Pq |
Вероятность того, что заявка окажется в очереди |
|
|
3 |
Lq |
Среднее число заявок в очереди (длина очереди) |
|
|
4 |
Ls |
Среднее число заявок в системе |
Ls = Lq + ρ |
|
5 |
Tq |
Среднее время пребывания заявки в очереди |
|
|
6 |
Ts |
Среднее время пребывания заявки в системе |
|
|
7 |
γ |
Отношение времени ожидания в очереди к времени обслуживания |
|
|
8 |
Q |
Относительная пропускная способность – вероятность того, что заявка будет обслужена |
Q = 1 |
|
9 |
A |
Абсолютная пропускная способность системы (среднее число заявок, обслуживаемых в единицу времени) |
A = λ Q = λ |
|
10 |
|
Среднее число занятых каналов |
|

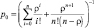
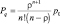
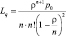
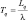 >
>