Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
3.2.1. Необходимые сведения и аналитические выражения
Основными характеристиками многоканальных систем массового обслуживания (СМО) с ожиданием [1] является вероятность p0 простоя системы и средняя длина Lq очереди:
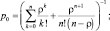(3)
|
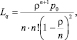
где n – |
число каналов обслуживания; |
|
|
коэффициент загрузки системы – отношение интенсивности входящего потока заявок к интенсивности их обслуживания в СМО. |
–Для формализации описания функционирования систем с ограниченным временем ожидания их удобно представлять в виде графа состояний, который в простейшем варианте является схемой гибели и размножения (см. рис. 3.3).
Рис. 3.3. Граф состояний СМО с ограниченным временем ожидания
В этом случае предельные вероятности определяются по следующим формулам:
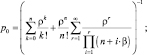(4)
|
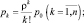
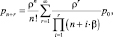
где β = |
|
|
ν – |
интенсивность уходящего (из очереди, не дождавшись обслуживания) потока заявок; |
|
r – |
число заявок, находящихся в очереди; |
|
k – |
число занятых каналов. |
;
Исследуем формулу (4) вероятности того, что система находится в состоянии S0 (все каналы свободны) [6]. Здесь в отличие от формулы (3) второе слагаемое в скобках есть бесконечный ряд, который не является прогрессией, но его элементы быстро убывают с ростом их номера.
Представим бесконечную сумму в виде двух слагаемых, в первом учитывается конечное число (q – 1) ее элементов, а второе (бесконечная сумма) – остаток.
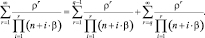(5)
Оценим остаток R, очевидно
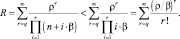
Можно показать, что
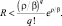(6)
Действительно
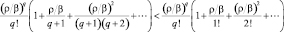
и, соответственно
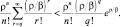
Длину очереди можно найти по формуле:
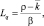
где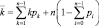 
– среднее число занятых каналов
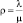