Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ ТРЕХМЕРНЫХ НЕСТАЦИОНАРНЫХ КОНВЕКТИВНЫХ ТЕЧЕНИЙ СЖИМАЕМОГО ВЯЗКОГО ТЕПЛОПРОВОДНОГО ГАЗА

Обухов А. Г., Сорокина Е. М.,

§1. Основные понятия и термины конвективного движения сплошной среды

В данном параграфе даются понятия, характеризующие движущуюся сплошную среду, формулируются уравнения движения жидкости под действием внешних и внутренних сил, а также тепловых источников. Этот классический раздел механики сплошной среды подробно излагается, например, в работах [1–6]. Следуя [7], приведем основные термины и гипотезы механики сплошной среды.

Основные гипотезы сплошной среды. Механика сплошных сред основана на справедливости:

1) классической механики Ньютона;

2) классической термодинамики;

3) гипотезы сплошности.

Классическая механика Ньютона предполагает, что изучаются движения со скоростями, малыми по сравнению со скоростью света, и рассматриваются макроскопические объекты, размеры которых существенно превосходят размеры микромира.

Классическая термодинамика предполагает, что в окрестности каждой точки среда находится в состоянии термодинамического равновесия или близкой к нему, вследствие чего можно пользоваться законами классической термодинамики.

Гипотеза сплошности предполагает замену реальной среды с ее дискретным молекулярным строением моделью сплошного распределения вещества по рассматриваемому объему.

Элементарная частица. Элементарной называется частица, размеры которой должны быть пренебрежимо малы по сравнению с характерными размерами изучаемого явления, но достаточно велики, чтобы не учитывать молекулярную структуру движущейся среды. В этом случае говорят о бесконечно малом объеме среды, эффективно равном нулю. При этом следует различать понятия точки пространства и элементарной частицы. Точка есть место в пространстве, а частица – малая часть материального объема. Совокупность элементарных частиц, во все время движения остающихся на одном контуре, поверхности или в объеме, называется, движущимся контуром, движущейся поверхностью или движущимся объемом соответственно.

Следует заметить, что принятие гипотезы сплошности как основы математического описания поведения движущихся сред означает, что функции, характеризующие их состояние, должны быть гладкими, то есть непрерывными и дифференцируемыми и по времени и по пространственным переменным.

Перейдем к определению некоторых фундаментальных величин механики сплошной среды.

Плотность. Плотность среды в данной точке находится как предел отношения массы, заключенной в некотором объеме среды, к величине этого объема, при условии стремления этого объема к нулю. Ее размерность в СИ [ρ] = кг/м3.

Объемные и поверхностные силы. Силы, действующие на сплошную среду, подразделяются на объемные и поверхностные. К объемным (массовым) силам принадлежат, например, силы тяжести, силы инерции, центробежная сила. Объемные силы действуют в каждой точке элементарного объема сплошной среды.

К поверхностным силам относятся силы, которые действуют на элемент поверхности, или часть граничной или любой внутренней поверхности. Поверхностные силы задаются тензором второго ранга (тензором напряжений). Это означает, что напряженное состояние в произвольной точке сплошной среды характеризуется девятью компонентами тензора напряжений Pij (i, j = 1, 2, 3).

Два способа описания движения сплошной среды. Переменные
(ξ1, ξ2, ξ3, t) называются переменными Лагранжа, а (x1, x2, x3, t) носят название переменных Эйлера. Основное отличие в описании движения в координатах Лагранжа и Эйлера заключается в том, что в первом случае величины (x1, x2, x3) – это переменные координаты движущихся частиц сплошной среды, во втором случае – это координаты фиксированных точек пространства, мимо которых в данный момент времени проходят различные частицы сплошной среды.

Интегральные законы сохранения. Важнейшими характеристиками материального объема являются его масса, импульс (количество движения), момент количества движения и полная энергия.

Из системы законов сохранения соответствующей механической величины вытекает система дифференциальных уравнений.

Уравнение неразрывности – дифференциальная форма закона сохранения массы

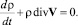(1.1)

Уравнение импульса – дифференциальная форма закона сохранения импульса

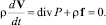(1.2)

Уравнение притока тепла – дифференциальная форма закона сохранения энергии

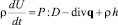. (1.3)

В уравнениях (1.1)–(1.3) t – время; V = (v1, v2,v3) – вектор скорости движения частиц среды; P – тензор напряжений; divP – есть вектор с компонентами

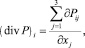(1.4)

где f – плотность массовых внешних сил; U – удельная внутренняя энергия; D – тензор скоростей деформаций с элементами

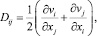i, j = 1, 2, 3; (1.5)

P:D – свертка тензоров P и D имеет вид

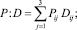(1.6)

q – вектор потока тепла; h – объемная плотность внутренних источников тепла. Первый дифференциальный оператор в уравнениях (1.1)–(1.3) – оператор 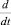 – носит название оператора полного дифференцирования по времени и состоит из суммы двух операторов – оператора локального частного дифференцирования по времени и оператора конвективного дифференцирования по времени. Например, полная производная по времени некоторой величины F может быть представлена в виде

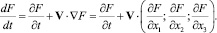(1.7)

Совокупность уравнений (1.1), (1.2), (1.3) образует математическую модель непрерывных движений сплошной среды. Эта модель не является замкнутой, так как содержит пять скалярных уравнений и четырнадцать (с учетом симметрии тензора напряжений P) искомых функций: ρ, v1, v2, v3, P11, P12, P13, P22, P23, P33, U, q1, q2, q3. Плотность массовых внешних сил f и объемная плотность внутренних источников тепла h считаются известными. Поэтому возникает проблема замыкания модели, которая должна решаться при анализе дополнительной информации.

Элементы термодинамики. Учет тепловой энергии в модели (1.1)–(1.3) требует привлечения законов термодинамики. Термодинамика изучает связи между тепловой энергией и другими видами энергии, в первую очередь механической энергией, и устанавливает закономерности взаимного превращения одного вида энергии в другой.

Основное понятие термодинамики – понятие состояния среды. Феноменологическое описание состояния идеальной сплошной среды осуществляется с помощью следующих пяти параметров состояния:

– удельная внутренняя энергия U [Дж];

– плотность ρ [кг/м3] или удельная плотность 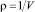, где V называется удельным объемом;

– абсолютная температура T [К];

– удельная энтропия s [Дж/(кг∙К)];

– давление p [Н/м2].

Если для сплошной среды такой набор параметров состояния установлен, то следующей задачей будет нахождение всех возможных соотношений между этими параметрами. Такие соотношения вытекают из общих физических законов и опытных закономерностей, описывающих поведение рассматриваемой сплошной среды. В первую очередь необходимо учесть законы термодинамики.

Первый закон термодинамики утверждает, что если в некотором элементарном физическом процессе сплошной среде сообщено количество тепла δQ, то она совершит механическую работу δA, а внутренняя энергия среды получит приращение dU, то есть всегда справедливо равенство

δQ = dU + δA. (1.8)

Этот физический закон, устанавливающий эквивалентность тепловой и механической энергии, является термодинамическим выражением закона сохранения энергии. Использование разных обозначений означает, что dU есть дифференциал U, а δQ и δA обозначают бесконечно малые количества теплоты и работы.

Второй закон термодинамики утверждает, что при любом процессе, идущем в теплоизолированной сплошной среде (без внешнего подвода или отвода тепла), энтропия этой среды не убывает, то есть для элементарных процессов

Tds ≥ δQ, (1.9)

где ds – дифференциал функции s. При этом процесс обратим, когда справедливо равенство Tds = δQ. Для таких процессов справедливо основное термодинамическое тождество

Tds = dU + pdV. (1.10)

В предположении, что идеальная сплошная среда двухпараметрическая и в последнем равенстве (1.10) стоят полные дифференциалы, то можно найти два соотношения между этими пятью параметрами состояния. Поэтому для полного описания термодинамического состояния такой двухпараметрической среды достаточно задать еще одно соотношение, которое называется уравнением состояния. В приложениях чаще всего используются уравнения состояния следующего вида:

– внутренняя энергия задается как функция объема V и энтропии s:

U = U(V, s); (1.11)

– теплосодержание (энтальпия) как функция от давления p и энтропии s:

I = I(p, s) = U + pV; (1.12)

– свободная энергия как функция от объема V и температуры T:

F = F(V, T) = U – Ts; (1.13)

– термодинамический потенциал как функция от давления p и температуры T:

Ψ = Ψ(p, T) = U – Ts + pV. (1.14)

Поскольку основной мерой количества тепла является температура, то потоки тепла и вызываются ее разностью. В термодинамике этот факт формулируется как закон Фурье:

q = –κ∇T, (1.14)

где κ – новый параметр состояния – коэффициент теплопроводности. Теперь уравнение притока тепла приводится к виду

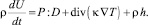(1.15)

Для полного замыкания системы дифференциальных уравнений механики сплошных сред требуется еще шесть уравнений. Эти уравнения, называемые также уравнениями состояния, связывают тензор напряжений с движением (или перемещением). Эти связи имеют различный вид для жидкостей и твердых тел и лежат в основе классических моделей сплошных сред – жидкостей и газов.

Классические модели жидкости и газа

Аксиомы Стокса. Газы и жидкости представляют собой легко подвижные сплошные среды, которые не остаются в равновесии, даже если на них действуют как угодно малые силы. Как показывает опыт, внутренние напряжения в жидкостях и газах существенно зависят от того, насколько быстро происходит деформация, то есть от скорости деформации. В феноменологической теории обычно дается следующее определение: жидкость или газ – это такая сплошная среда, в которой тензор напряжений P является функцией тензора скоростей деформации D. Тензор напряжений также может зависеть от совокупности термодинамических параметров состояния, от местоположения точки пространства x = (x1, x2, x3) и времени t, то есть

P = f(D, ρ, U, T, s, p, x, t). (1.16)

Для жидкостей и газов предполагается выполнение аксиом Стокса, которые конкретизируют зависимость (1.16):

– среда однородна, то есть f не зависит явно от величин x, t;

– среда изотропна, то есть f является изотропной тензорной функцией тензора скоростей деформации D;

– покоящаяся среда идеальна, то есть

P = f(0, ρ, U, T, s, p) = –pI, (1.17)

где p – давление; I – единичный тензор.

Изотропность тензорной функции f приводит к зависимости

P = αI + βD + ζD2, (1.18)

где α, β, ζ являются функциями инвариантов тензора скоростей деформации D и термодинамических параметров состояния.

Термодинамическое состояние жидкостей и газов достаточно хорошо описывается равенством (1.10), которое справедливо лишь для обратимых процессов. Классическая термодинамика рассматривает состояния среды, близкие к равновесным, и взаимные превращения одного вида энергии в другой в этих состояниях. Жидкости и газы обычно считаются двухпараметрическими средами, что выполняется при рассмотрении однофазных однокомпонентных движений.

Если независимыми параметрами считать плотность ρ и удельную энтропию s, тогда задается удельная внутренняя энергия U = U(ρ, s) и из (1.10) следуют формулы

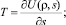
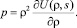(1.19)

Коэффициент теплопроводности κ, входящий в уравнение притока тепла (1.15), также считается известной функцией параметров состояния κ = κ(ρ, s).

Иногда считают независимыми параметрами состояния абсолютную температуру и плотность, то есть задается U = U(ρ, T). Тогда из (1.10) следует

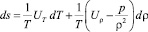(1.20)

и выражение в правой части этого тождества будет полным дифференциалом, если существует функция f(T, ρ) (свободная энергия) такая, что

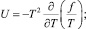p = ρ2fρ, (1.21)

а κ = κ(ρ, T).

Практический интерес представляет теплоемкость, то есть, количество тепла, которое необходимо сообщить единице массы, чтобы увеличить ее температуру на один градус при обратимом изменении состояния 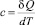. Различают удельные теплоемкости при постоянном давлении cp и при постоянном объеме cV:

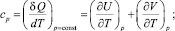(1.22)

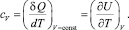(1.23)

Здесь учтен закон сохранения (1.10). Введение энтропии дает возможность получить и другие выражения для удельных теплоемкостей. Действительно, поскольку для обратимых процессов Tds = δQ, то

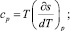
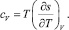(1.24)

Замкнутая модель, основанная на аксиомах Стокса, состоит из уравнений (1.1), (1.2), (1.15), (1.18) содержит пять уравнений относительно пяти неизвестных функций – трех компонент вектора скорости и двух независимых параметров состояния. Тем не менее, эта модель очень редко рассматривается в качестве рабочей, поскольку требует очень большой объем дополнительной информации для определения коэффициентов α, β, ζ в (1.18).

Ньютоновские сплошные среды. Более употребительной и достаточно общей является классическая модель сплошной среды. Она основана на том, что зависимость тензора напряжений (1.18) линейна

P = αI + βD. (1.25)

Такие сплошные среды называют ньютоновскими. При этом

ζ = 0; α = –p + λdiv V; (1.26)

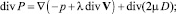(1.27)

P:D = –pdiv V + Φ, (1.28)

где диссипативная функция

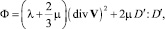(1.29)

а

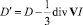(1.30)

девиатор тензора D. Кроме того, введено обозначение 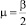. Учитывая, что

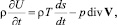(1.31)

получим классическую модель движения ньютоновской сплошной среды

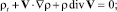(1.32)

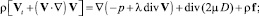(1.33)

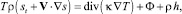(1.34)

в которой λ, μ, κ считаются известными функциями двух независимых параметров состояния, а p, ρ, s, T связаны двумя соотношениями (1.19) или (1.21). Данная модель замкнута, а коэффициенты λ и μ называются коэффициентами динамической вязкости и отражают свойства сплошной среды сопротивляться сдвиговым усилиям.

Из модели (1.32)–(1.34) получаются хорошо известные и достаточно простые частные модели сплошной среды.

Модель идеальной несжимаемой жидкости. В этом случае μ = 0, а условие несжимаемости ρ = const эквивалентно

div V = 0; D′ = D, (1.35)

а модель (1.32)–(1.34) значительно упрощается и приводится к виду:

div V = 0; (1.36)

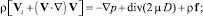(1.37)

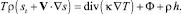(1.38)

Модель вязкой несжимаемой жидкости. В этой модели в термодинамическом отношении среда становится однопараметрической, поскольку давление p исчезает из термодинамических соотношений (так как pdV = 0) и не может рассматриваться как параметр состояния. Остается только один параметр состояния – температура T. Введя кинематическую вязкость 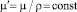и преобразовав слагаемое в уравнении импульса (1.37) так:

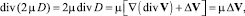(1.39)

где 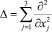 – оператор Лапласа, приходим к модели вязкой несжимаемой жидкости

div V = 0; (1.40)

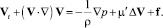(1.41)

Систему уравнений (1.40), (1.41) называют также системой Навье – Стокса, в которой термодинамика вообще не представлена. Температуру T можно определить из уравнения притока тепла (1.38), которое можно переписать в виде

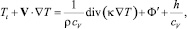(1.42)

где

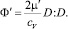(1.43)

В этой модели сплошная среда описывается двумя величинами – вязкостью μ′ и плотностью ρ, которые определяются из эксперимента.

Модель идеальной жидкости. Если вязкость сплошной среды несущественна, то μ′ = 0 и система уравнений в данной модели будет иметь вид:

div V = 0; (1.44)

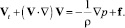(1.45)

Эта система называется системой уравнений Эйлера. Уравнение для температуры упрощается, если предположить, что коэффициент теплопроводности κ и удельная теплоемкость при постоянном объеме cV постоянные. В этом случае уравнение притока тепла приобретает вид:

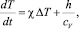(1.46)

где 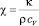 – коэффициент температуропроводности.

Система уравнений газовой динамики. В отличие от жидкостей, газы являются сильно сжимаемыми средами, и вязкость газа часто бывает несущественна. Для быстропротекающих процессов в газе можно пренебречь и теплопроводностью. Принимая в (1.29), (1.32)–(1.34) λ = μ = κ = 0, получаем систему уравнений газовой динамики:

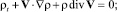(1.47)

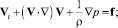(1.48)

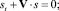(1.49)

p = f(ρ, s), (1.50)

где последнее соотношение называется уравнение состояния газа.

Диссипация энергии. Свойства вязкости и теплопроводности жидкостей и газов проявляются в том, что сообщенная среде механическая энергия может необратимым образом перейти в тепловую, рассеяться в хаотическом тепловом движении молекул. Это рассеяние механической энергии называется диссипацией, а процессы, сопровождаемые диссипацией энергии – диссипативными процессами.

С точки зрения термодинамики, диссипативный процесс необратим и должен сопровождаться возрастанием энтропии. Обратно, рост энтропии какой-либо части сплошной среды, происходящий без «подкачки» тепловой энергии извне, служит признаком того, что в этой части среды идет диссипативный процесс.

В общем случае кинетическая энергия движущегося объема убывает. Это и есть проявление диссипативного процесса в вязкой несжимаемой жидкости, за который отвечает коэффициент вязкости μ.

Диссипативная функция Φ равна плотности скорости диссипации кинетической энергии. Этим, в частности, оправдано название «диссипативная функция» для величины Φ.