Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Прикладные методы оптимизации

Шукаев Д. Н.,

5.2.2. Метод штрафных функций

Метод штрафных функций является одним из наиболее простых и широко применяемых методов решения нелинейных задач оптимизации. Идея метода основана на преобразовании исходной задачи с ограничениями в одну или последовательность задач безусловной оптимизации. Суть такого преобразования заключается в следующем. С помощью функций, задающих ограничения, строится так называемый штраф, который добавляется к целевой функции исходной задачи так, чтобы нарушение какого-нибудь ограничений становилось невыгодным с точки зрения полученной задачи безусловной оптимизации.

Рассмотрим задачу определения максимального значения вогнутой функции

f(x) → max

при ограничениях

g(x) ≤ b, x ≥ 0,

где g(x) – выпуклая функция.

В соответствии с идеей метода штрафных функции исходную задачу условной оптимизации преобразуем в задачу безусловной оптимизации

F(x) = f(x) + H(x).

Штрафная функция H(x) определяется ограничениями исходной задачи и имеет вид

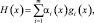
где параметры α_i(x) играют роль весовых коэффициентов. Излишне говорить, что штраф желателен только в недопустимых точках, поэтому

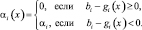
Процесс нахождения оптимального решения исходной задачи состоит в использовании штрафной функции для последовательного перехода из одной точки к другой, пока не получат приемлемое решение. Координаты последующей точки находят по формуле

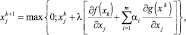(5.18)

где λ ∈ [0; 1]. Из этого выражения следует, что если предыдущая точка находится в области допустимых решений исходной задачи, то второе слагаемое в квадратной скобке равна нулю и переход к последующей точке определяется только градиентом целевой функции. Если же эта точка не принадлежит области допустимых решений, то за счет этого слагаемого на последующих итерациях достигается возвращение в область допустимых решений. При этом чем меньше α_i, тем быстрее находится приемлемое решение, однако точность его определения снижается. Поэтому итерационный процесс обычно начинают при малых α_i и продолжая его α_i постепенно увеличивают.

Укрупненный алгоритм метода штрафных функций состоит из следующих шагов.

Шаг 0. Определение исходного допустимого решения.

Шаг 1. Выбирают шаг вычислений.

Шаг 2. Находят частные производные от целевой функции f(x) и функции g(x).

Шаг 3. По формуле (5.18) находят координаты точки, определяющей возможное новое решение задачи.

Шаг 4. Новую точку проверяют на допустимость по ограничениям исходной задачи. Если нет, то переход на шаг 5. При допустимости найденного решения исследуется необходимость перехода к следующему допустимому решению. При необходимости такого перехода возврат на шаг 1. В противном случае найдено приемлемое допустимое решение исходной задачи.

Шаг 5. Устанавливают значения α_i и переходят на шаг 3.

Пример 5.3. Необходимо максимизировать целевую функцию

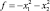(5.19)

при ограничениях

(x1 – 7)² + x2 – 7)² ≤ 18, x1, x2 ≥ 0. (5.20)

Решение. Целевая функция данной задачи – отрицательно-определенная квадратичная функция и, следовательно, вогнута, а область допустимых решений – выпукла. Следовательно, эта задача является задачей выпуклого программирования для уяснения процесса поиска оптимального решения дадим геометрическую интерпретацию этой задачи. Построим область допустимых решений (рис. 5.1), определяемой ограничениями (5.20) и линии уровня, определяемые целевой функцией (5.19). Этими линиями служат окружности с центром в точке (0; 0). Точка касания одной из этих окружностей с областью допустимых решений в виде круга с центром в точке Е и является искомой точкой максимального значения целевой функции.

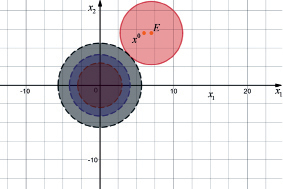
Рис. 5.1. Геометрическая интерпретация задачи

Для решения этой задачи воспользуемся методом штрафных функций.

Шаг 0. За исходное допустимое решение примем x⁰ = (6; 7).

Шаг 1. Шаг вычислений выберем равным λ = 0,1.

Шаг 2. Представив функцию ограничения в виде

g(x) = 18 – (x₁ – 7)2 + (x₂ – 7)²

и определим частные производные от f(x) и g(x)

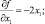
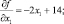
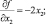
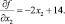
Теперь используя формулу (5.18) приступим к построению последовательности точек.

Итерация 1.

Шаг 3. Так как x0 = (6; 7) принадлежит области допустимых решений, то второе слагаемое в квадратной скобке формулы (5.18) равен нулю. Тогда координаты следующей точки x1 вычисляем по усеченной формуле (5.18)

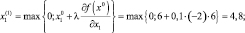
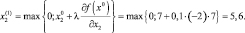
Шаг 4. Полученное решение проверяем на допустимость по ограничениям исходной задачи

g(x¹) = (4,8 – 7)² + (5,6 – 7)² = (–2,2)² + (–1,4)² = 6,8 < 18.

Полученное решение является допустимым, а значение целевой функции.

Итерация 2.

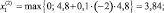
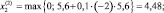
g(x²) = (3,84 – 7)² + (4,48 – 7)² < 18; f = –34,816.

Итерация 3.

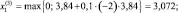
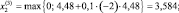
g(x3) = (3,072 – 7)2 + (3,584 – 7)2 > 18.

Итерация 4. Полученное на итерации 3 решение не является допустимой, поэтому для определения нового решения используем формулу (5.18) с учетом второго слагаемого квадратной скобки

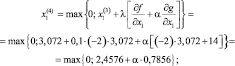
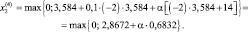
Здесь возникает вопрос о выборе числа α. Существует два подхода такого выбора. В первом случае надо взять значение α таким, чтобы точка x⁽⁴⁾ не слишком далеко удалилась от границы области допустимых решений и вместе с тем принадлежала этой области. Такой достаточно произвольный выбор α зачастую увеличивает число итераций. Во втором случае используется формула Эрроу – Гурвица

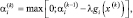i = 1, …, m,

где в качестве начального значения α берут любое неотрицательное число.

Воспользуемся вторым подходом, тогда

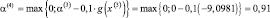
и по формуле (5.18) получим

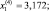
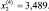
При этом g(x⁽⁴⁾) ≈ –8,181.

Продолжая таким образом находим приемлемое решение, когда, либо ограничение будет выполняться почти как равенство, либо, когда значения целевой функции для соседних итераций будут отличаться между собой на незначительную величину.

Эту задачу можно остановить на 13-й итерации когда

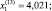
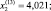
g(x⁽¹³⁾) ≈ 0,251; f(x⁽¹³⁾) = –32,337.