Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Определение оптимального парка воздушных судов.

Припадчев А. Д.,

3.4 Формирование параметров эффекта системы

Математическая модель параметрического синтеза устанавливает взаимосвязи множеств режимных параметров (РП), конструктивно-геометрических (КГП), инерционно-массовых (ИМП), физико-механических (ФМП), технологических (ТП) с множеством параметров эффекта выделенных для данного процесса через внутреннюю характеристику системы Э - экономическую эффективность [121, 138], в соответствии с рисунком 3.1:

1) приведенные затраты - а_ПР;

2) расход топлива - С_РКРЕЙС;

3) производительность воздушного судна - А;

4) интенсивность движения на линии - N.

Приведенные затраты, в рублях на тонно-километр, выраженные относительно одного самолета вычисляем по формуле

,                                      (3.48)

где    а - себестоимость перевозок, р./(т км);

а_КАП.ВЛ - приведенные капиталовложения, р./(т км).

Удельный расход топлива, килограмм топлива на один ньютон тяги в час, вычисляем по формуле

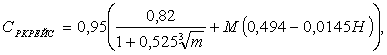               (3.49)

где    т - степень двухконтурности двигателя;

М - число М полета;

Н - высота полета, км.

Производительность воздушного судна, в килограммах на час, вычисляем по формуле

,                                          (3.50)

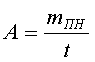
где    m_ПН - масса полезной нагрузки перевозимой воздушным судном, кг;

t - время полета, ч.

Интенсивность движения на линии, в процентах, вычисляем по формуле

,                       (3.51)

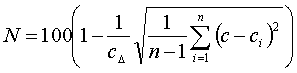
где    п - количество отобранных воздушных судов;

c_i - количество контрольных воздушных судов в i-серии, %;

- среднеарифметическое значение контрольного компонента (воздушного судна), %.

Используя зависимость (3.48)-(3.51) и решенное уравнение Колмогорова-Фоккера-Планка (3.46), возможно определить экономическую эффективность процесса пассажирских перевозок гражданской авиации.

Математическая модель, сформированная из предлагаемых независимых множеств параметров (РП, КГП, ИМП, ФМП, ТП) на базе внутренней характеристике системы, позволяет разработать оптимальные критерии процесса пассажирских перевозок гражданской авиации.