Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Определение оптимального парка воздушных судов.

Припадчев А. Д.,

3.5 Обработка данных процесса пассажирских перевозок гражданской авиации

Проверка достоверности математической модели является необходимым условием правомерности его использования в научных и технических исследованиях. Особое значение имеет проверка для априорной информации. Возможны следующие методы проверки априорной информации:

• 1) сравнение результатов с точными решениями. Это позволяет определить истинную ошибку вычислительного метода. Недостаток этого метода заключается в ограниченном количестве геометрических параметров;
• 2) анализ выполнения точных теоретических соотношений;
• 3) графическое сопоставление расчетных данных с экспериментальными. Критерием достоверности служит качественная «близость» результатов эксперимента и расчета;
• 4) статистический анализ на основе регрессионных методов;
• 5) статистический анализ по методу наименьших квадратов;
• 6) обобщенная статистическая проверка математической модели воздушного судна.

Перечисленные методы позволяют проверить достоверность, как отдельных элементов математической модели воздушного судна, так и математической модели процесса воздушной перевозки в целом.

 Из вышесказанного следует что, экономическая эффективность системы зависит от множества параметров и решение уравнения это сложная задача, поэтому целесообразнее было бы заменить его более простыми приближенными уравнениями, т.е. аппроксимировать уравнениями регрессии. Уравнения регрессии - это зависимость какого-либо значения случайной величины от некоторой детерминированной величины или нескольких величин. Основа регрессионного анализа лежит на аппроксимации статистических данных и финансовых отчетов авиакомпаний алгебраическими полиномами.

Для нахождения коэффициентов уравнения регрессии необходимо составить матрицу значений [9, 40, 64, 48], характеризующих процесс пассажирских перевозок, и воспользоваться методом наименьших квадратов. Необходимые параметры, влияющие на экономическую эффективность, представлены в соответствии с таблицей 3.1.

Исходя из вышесказанного, следует, что экономическая эффективность системы Э, обозначенная как Y1 зависит от

,                           (3.52)

Таблица 3.1 - Параметры, влияющие на экономическую эффективность

Параметры процесса	Обозначение	Единицы измерения	Символы обозначения
1	2	3	4
Масса воздушного судна	mО	кг	Х1
Скорость полета	VКРЕЙС	км/ч	Х2
Удельный расход топлива	СРКРЕЙС	кг/Н ч	Х3
Параметр оценки пассажирского воздушного судна	Y	р.	Х4
Высота полета	НЭ	М	Х5
Аэродинамическое качество воздушного судна	К	-	Х6

Для решения подобных задач используются полиномы п-ой степени. Ограничимся полиномом 3-ей степени, коэффициенты которого определяются решением матричного уравнения

,                                    (3.53)

где    В - вектор коэффициентов уравнения;

Х - матрица «плана экспериментов»;

Y^/ - вектор значения параметра.

Адекватность модели проверяется по критерию Фишера [21] определяемому для экономической эффективности системы.

Получено уравнение регрессии для экономической эффективности системы, которую вычисляем в соответствии с уравнением

  ,            (3.53)

Табличное значение критерия экономической эффективности Э=0,0017, при принятом уровне значимости , критерий Фишера Ф=1,96, уравнение адекватно [17].

Из полученного уравнения регрессии видно, что модель в полном объеме описывает процесс пассажирских перевозок, а также показано влияние и связь экономической эффективности с режимными, конструктивно-геометрическими, инерционно-массовыми, физико-механическими и технологическими параметрами.

Помимо метода наименьших квадратов для определения линейных связей между параметрами наблюдений возможно применение факторного анализа. Одним из методов факторного анализа является метод главных компонентов. Данный метод основан на расчленении корреляционной матрицы на совокупность компонентов.

Для построения нелинейных моделей прогноза одних показателей по другим используют уравнения ступенчатого регрессионного метода. При определении таких зависимостей возможно два направления:

1) чтобы уравнение было полезным для практического использования, необходимо стремиться включить в него как можно больше переменных, чтобы определение одних показателей по другим стало более достоверным;

2) поскольку затраты на получение информации и контроль при большем числе переменных велики, необходимо стремиться к тому, чтобы модель включала как можно меньше величин.

Первым этапом исследования многопараметрических процессов является отбор параметров. Из всех возможных параметров ранговыми методами производят ранжирование и априорное отсеивание. Обработку целесообразно вести, производя предварительно центрирование и нормирование результатов наблюдения. Для отыскания оптимальных условий протекания сложных многопараметрических процессов применяем полиноминальные математические модели процесса, в соответствии с формулой

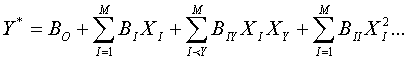,             (3.54)

где    Y^* - параметр оптимизации;

B_O, B_I, , B_II - выборочные коэффициенты регрессии, полученные по результатам эксперимента;

X_I, - параметры и их взаимодействия.

Теоретически коэффициенты уравнения регрессии можно определить из системы нормальных линейных уравнений.

Для упрощения определения коэффициентов уравнения регрессии используем формулу

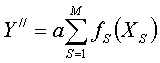,                                     (3.55)

где    - любая функция величины .

Из расчетов следует, что коэффициент детерминации близок к единице. Это говорит об адекватности модели истинной зависимости и подтверждается невысокими значениями средних ошибок.

Для проведения предварительной обработки необходимо иметь матрицу наблюдений, состоящую из строчек - соответствующих наблюдений, и столбика - исследуемый показатель. В матрице наблюдений определяют следующие основные характеристики параметров - столбиков:

1) статистическое распределение - это частота встречаемости каждого значения выборки. Каждое значение выборки и соответствующие им частоты заносят в таблицу. В таблице X_i - значение выборки, в математической статистике называется вариантами;

2) выборочное среднее, вычисляем в соответствии с формулой

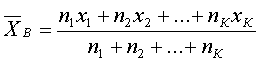,                              (3.56)

Выборочное среднее есть значение оценки математического ожидания нормально распределенной случайной величины, вычисляем по формуле

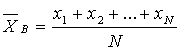,                                   (3.57)

• 1) выборочная дисперсия, вычисляем по формуле

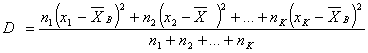,                 (3.58)

4) выборочное среднее квадратичное отклонение, вычисляем по формуле

,                                         (3.59)

5) доверительный интервал для оценки математического ожидания, вычисляем по формуле

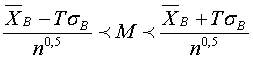,                         (3.60)

При известном значении σ величину Т находим из равенства

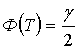,                                          (3.61)

где    Ф - функция Лапласа;

γ - доверительная вероятность, ;

п - число наблюдений;

Т - значение случайной величины, имеющей распределение Стьюдента;

6) мода М_О - это варианта, которая имеет наибольшую частоту, т.е. для определения моды необходимо в массиве частот п₁, п₂, ...п_К найти максимальную. Соответствующая этой частоте варианта и будет модой;

7) медианой т_Е называют варианту, которая делит вариационный ряд на две части, равные по числу вариант, ее вычисляем по формуле

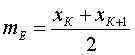,                                      (3.62)

8) размахом варьирования R называют разность между наибольшей и наименьшей вариантами, вычисляем по формуле

,                                  (3.63)

9) средним абсолютным отклонением  называют среднее арифметическое абсолютных отклонений, вычисляем по формуле

,                   (3.64)

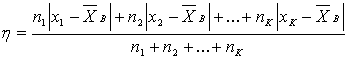
10) коэффициентом вариации V называют выраженное в процентах отношение выборочного среднего квадратичного отклонения к выборочной средней, вычисляем по формуле

,                                       (3.65)

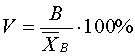
11) асимметрию эмпирического распределения вычисляем в соответствии с равенством

,                                              (3.66)

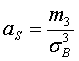
где т₃ - центральный эмпирический момент третьего порядка, вычисляем в соответствии с формулой

,              (3.67)

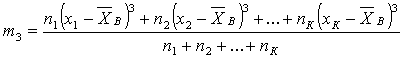
Если абсолютная величина асимметрии близка к нулю, то можно считать статистическое распределение нормальным. Для более точной проверки гипотезы о нормальности статистического распределения следует воспользоваться критерием «Х_i квадрат»;

12) эксцесс эмпирического распределения вычисляем по формуле

,                                         (3.68)

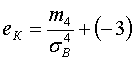
где т₄ - центральный эмпирический момент четвертого порядка, вычисляем по формуле

,           (3.69)

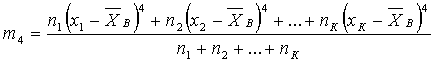
Если модуль эксцесса близок к нулю, то можно считать статистическое распределение нормальным. Для более точной проверки гипотезы о нормальности статистического распределения следует воспользоваться критерием «Х_I квадрат»;

13) гистограмма плотности абсолютных и относительных частот. Для построения гистограммы плотности абсолютных и относительных частот весь интервал, в котором заключены все варианты, разбиваем на несколько частичных интервалов длиною «h» и находим для каждого интервала c_I - сумму частот, попавших в I-ый интервал.

Гистограммой плотности абсолютных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною «h», а высоты равны с_I / h. Площадь гистограммы абсолютных частот равна сумме всех частот, т.е. объему выборки;

14) принадлежность к нормальному распределению. Проверка гипотезы о предполагаемом законе неизвестного распределения производится при помощи специально подобранной случайной величины - критерия согласия. Для проверки гипотезы о нормальном распределении выборки применяют критерий Пирсона «Х_I квадрат». С этой целью сравниваем эмпирические (наблюдаемые) и теоретические (вычисленные в предположении нормальности) частоты. При п - выборке объема, стремящаяся к бесконечности, закон распределения случайной величины вычисляем по формуле

,                                            (3.70)

где P_I - интеграл вероятности попадания.

Независимо от того, к какому закону распределения подчинена генеральная совокупность, при п - выборке объема, случайная величина стремиться к закону распределения «Х_I квадрат» с «k» степенями свободы.