
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
4.4 Оптимальный парк воздушных судов гражданской авиации на основе параметрического ряда
Воздушное судно характеризуется большим количеством параметров - весовых, геометрических, аэродинамических, о чем уже упоминалось в третьей главе. При оптимизации парка ВС необходимо провести увязку параметров ВС с процессом пассажирских перевозок, чем эффективнее будет произведена увязка, тем экономически выгоднее окажется процесс.
Из вышесказанного следует, что для осуществления процесса пассажирских перевозок с минимальными затратами необходимо иметь ВС, которые возможно оценить, построив параметрический ряд, основанный на прогнозе развития отечественного и мирового самолетостроении.
Исходные данные для расчета параметрических рядов могут быть заданы на определенный, довольно длительный перспективный период, обусловленный планированием исходных показателей. Следовательно, для каждого следующего периода должны быть разработаны новые параметрические ряды применительно к условиям нового периода.
Решение задачи оптимизации перспективных параметрических рядов связано с рассмотрением сложной динамической стохастической системы. Сложность системы определяется большим количеством взаимосвязанных факторов в системе. Динамический характер данной системы заключается в том, что в течение перспективного периода, на который определяется параметрический ряд, происходит изменение объема пассажирских перевозок, условий их выполнения и следовательно, количества ВС в парке.
Однако возникают сложности учесть факторы, связанные с ВС, трудность получения необходимой информации, количественно характеризующей те или иные факторы. Все это говорит о необходимости на данном этапе рассматривать статическую задачу для определенного отрезка времени.
Составление параметрического ряда заключается в определении основных характеристик ВС, и с помощью математических методов определяется оптимальное ВС на каждом конкретном маршруте.
В работе был рассмотрен параметрический ряд двух авиакомпаний, с имеющимся парком ВС.
Выбор оптимального парка ВС с учетом тактико-технических характеристик, воздушного сообщения, количества пассажиров в ВС, количества рейсов в месяц и затраченных расходов на I-ом маршруте в месяц производим комплексно с помощью симплекс-метода. Информация, которую можно получить с помощью симплекс-метода, не ограничивается лишь оптимальными значениями переменных [20, 24, 45, 46, 130]. Симплекс-метод позволяет дать экономическую интерпретацию полученного решения и провести анализ модели на чувствительность. Анализ модели на чувствительность это процесс, реализуемый после того, как оптимальное решение получено. В рамках такого анализа выявляется чувствительность оптимального решения к определенным изменениям исходной модели.
Процесс решения задачи линейного программирования симплекс-методом носит итерационный характер, т.е. однотипные вычислительные процедуры в определенной последовательности повторяются до тех пор, пока не будет получено оптимальное решение. Процедуры, реализуемые в рамках симплекс-метода, естественно требуют применения персональных ЭВМ. В вычислительной схеме симплекс-метода реализуется упорядоченный процесс, при которой, начиная с некоторой исходной допустимой точки осуществляются последовательные переходы от одной допустимой экстремальной точки к другой до тех пор, пока не будет найдена точка (тип ВС на маршруте), соответствующая оптимальному решению.
Исходной точкой при определении оптимального парка ВС является начальное решение. От исходной точки осуществляется переход к следующей смежной точки. Выбор точки зависит от коэффициентов целевой функции, где коэффициент больше функция подлежит максимизации, что приводит к экстремальной точке. После чего указанный процесс повторяется, для выяснения существует ли другая экстремальная точка, соответствующая лучшему допустимому решению. В результате такой итеративный процесс позволяет найти оптимальное ВС для соответствующего маршрута.
Выбор каждой последующей экстремальной точки при использовании симплекс метода определяется следующими правилами:
1) каждая последующая точка должна быть смежной с предыдущей;
2) обратный переход к предшествующей экстремальной точке не может производиться.
Блок-схема симплекс-метода в первой канонической форме представлена в соответствии с рисунком 4.3.
Симплекс-алгоритм состоит из следующих этапов:
1) используя линейную модель стандартной формы, определяем начальное допустимое базисное решение путем приравнивания к нулю небазисных переменных;
2) из числа текущих небазисных (равных нулю) переменных выбирается включаемая в новый базис переменная, увеличение которой обеспечивает улучшение значения целевой функции. Если такой переменной нет, вычисления прекращаются, т.к. текущее базисное решение оптимально. В противном случае осуществляется переход к следующему этапу;
3) из числа переменных текущего базиса выбирается исключаемая переменная, которая должна принять нулевое значение (стать небазисной) при введении в состав базисных новой переменной;
4) находится новое базисное решение, соответствующее новым составам небазисных и базисных переменных. Осуществляется переход к этапу «2».
Схема алгоритма выбора оптимального парка ВС с помощью симплекс-метода представлена в соответствии с рисунком 4.4.
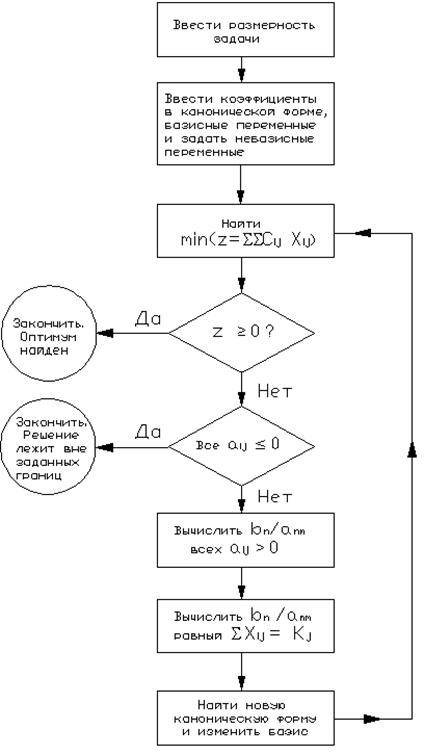
Рисунок 4.3 - Блок схема симплекс-метода
Из теоретических положений, лежащих в основе построения симплекс-метода, следует, что угловая точка полностью определяется базисным решением задачи линейного программирования. Условия оптимальности и допустимости симплекс-алгоритма обеспечивает переход от начальной допустимой точки (начального базисного решения) к смежной точке, соответствующей улучшенному значению целевой функции. Максимальное количество итераций, необходимых для получения оптимума (т.е. количество базисных решений), не превосходит ![]() , где N - число переменных, а M - число уравнений модели линейного программирования, представленной в стандартной форме.
, где N - число переменных, а M - число уравнений модели линейного программирования, представленной в стандартной форме.
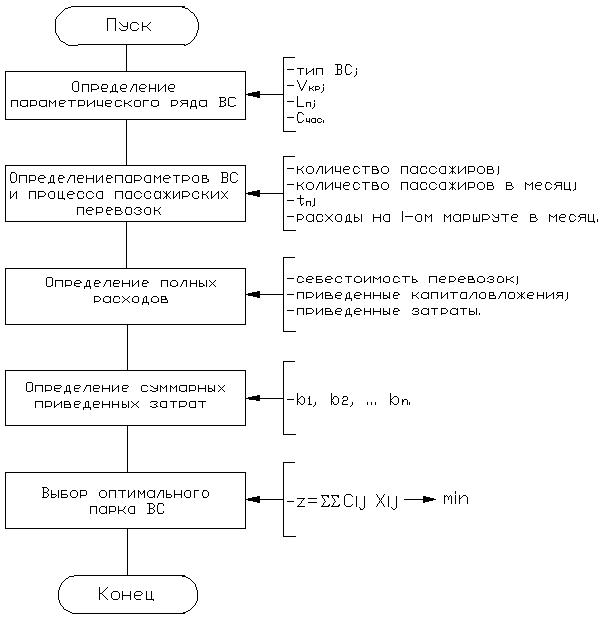
Рисунок 4.4 - Схема алгоритма выбора оптимального парка ВС
