Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

ПОСТРОЕНИЕ ИНФОРМАЦИОННЫХ СИСТЕМ НЕПРЕРЫВНОГО ОБРАЗОВАНИЯ НА ОСНОВЕ ИНТЕРНЕТ-ТЕХНОЛОГИЙ

Дьяченко А. В., Манжула В. Г., Попов А. Э., Семенихин И. Н., Толстобров А. П.,

2.3 Возможности анализа и повышения качества тестовых заданий при использовании сетевой системы управления обучением Moodle

Широкое использование электронных систем управления обучением не в последнюю очередь обусловлено наличием в них средств, позволяющих сделать более технологичной важнейшую составляющую процесса обучения, связанную с оценкой уровня освоения учащимися изучаемого учебного ма­териала. Речь идет об использовании автоматизированных тестовых систем в качестве средства измерения уровня подготовки учащихся.

Для этих целей в системе Moodle, как и в других современных системах аналогичного назначения, имеется подсистема, позволяющая формировать банки тестовых заданий всех основных форм - «в закрытой форме», «вычис­ляемые», «короткий ответ», «числовые», «на соответствие», «вложенные от­веты», и строить из них тесты, предназначенные для самоконтроля и тренинга, тематические тесты, тесты для текущей и итоговой оценок уровня обу­чаемых и др.

Для преподавателя, использующего такого рода средства при препода­вании своих учебных курсов, большая доля его труда состоит в создании банка тестовых заданий, обеспечивающего решение задачи оценки успешно­сти освоения обучаемыми представляемого им учебного материала. При этом неизбежно возникает вопрос о качестве разработанных и используемых тес­товых заданий с точки зрения их способности адекватно решать задачу изме­рения уровня подготовки испытуемых, правильно дифференцировать их в соответствии с действительным уровнем их подготовки. Дело в том, что тес­товые задания, удовлетворяющие формальным требованиям, например, пра­вильность формы, логическая точность и непротиворечивость высказываний и др., на практике могут не обладать качествами, позволяющими рассматри­вать их как полноценное средство измерения уровня подготовки испытуемых.

Вообще говоря, вопрос о способности конкретных контрольно-измерительных материалов в действительности служить средством измере­ния уровня подготовки обучаемых, имеет место при использовании любой системы оценивания, в том числе и при использовании традиционных экза­менационных испытаний в устной или письменной форме. Но именно при использовании автоматизированных тестовых систем возникает возможность реального применения для оценки качества используемых контрольно-измерительных материалов формализованных подходов, основанных на ме­тодологии теории педагогических измерений. Становятся возможными нако­пление и статистическая обработка результатов испытаний и получение ко­личественных характеристик, позволяющих оценивать качество тестовых контрольно-измерительных материалов.

Один из известных подходов для такого анализа базируется на извест­ной в теории педагогических измерений однопараметрической модели Раша.

Практическое использование предлагаемых этой теорией подходов об­легчается тем, что в системе управления обучением Moodle имеются развитые встроенные средства для автоматизации вычисления по результатам вы­полнения тестовых заданий статистических показателей, позволяющих осу­ществлять объективную оценку качества тестовых заданий с точки зрения их способности служить средством измерения уровня подготовки испытуемых.

Для осуществления Moodle такой обработки результатов тестирования необходимо на вкладке просмотра результатов тестирования (рис. 44) перей­ти к пункту Анализ вопросов.

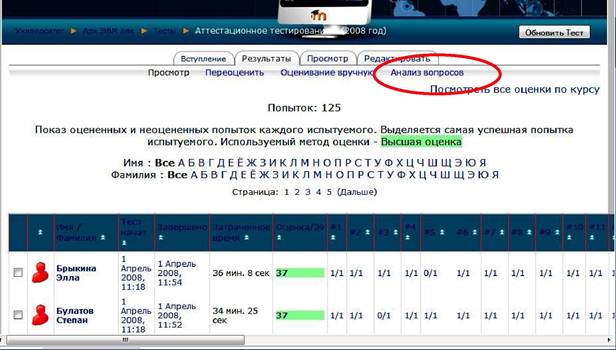
Рис. 44. Скриншот системы Moodle со списком испытуемых, прошедших тестирование, и полученных ими результатов

Обработка результатов испытаний, необходимая для получения харак­теристик качества тестовых заданий состоит в следующем.

В соответствии с педагогической теорией измерений полученные ис­пытуемыми результаты испытаний представляются в виде матрицы следую­щего вида (рис. 45).

Рис. 45. Матрица результатов тестовых заданий

В столбцах этой матрицы находятся результаты, полученные конкрет­ными испытуемыми по каждому тестовому заданию, а по строкам размеща­ются результаты каждого испытуемого по соответствующему тестовому за­данию. В нижней строке представлены суммарные значения баллов, набран­ных каждым испытуемым за тест в целом (S_i = ∑x_{i j}). Эти значения исполь­зуются для формирования оценки уровня подготовки испытуемых по прове­ряемому данным тестом учебному материалу. В правом столбце приведены суммы баллов, полученных всеми испытуемыми для каждого тестового зада­ния (для j-го задания - P_j = ∑x_{i j}). По величине значений P_j уже можно су­дить о степени реальной легкости (трудности) конкретных тестовых заданий для испытуемых в данной группе - чем больше испытуемых правильно от­ветило на конкретное задание, тем это задание в среднем легче для выполне­ния. Для практического использования, однако, в качестве меры легкости (трудности) заданий более пригодны относительные значения такого рода показателей. Это - индекс легкости задания (ИЛ) и индекс трудности зада­ния (ИТ):

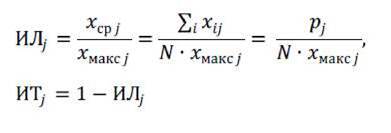
где x_{ср j} - среднее значение баллов, набранных всеми испытуемыми за вы­полнение j-го задания, x_{макс j} - максимально возможное количество баллов за выполнение j-го задания.

Эта характеристики (ИЛ и ИТ) тестовых заданий являются мерой лег­кости (трудности) заданий для конкретной группы испытуемых. Значения этих параметров зависят от уровня подготовки испытуемых и не зависят от их числа. Одно из положений педагогической теории измерений состоит в том, что в тесте не должно быть заданий неизвестной трудности. Важ­ность получения количественных характеристик легкости (трудности) пред­лагаемых испытуемым заданий состоит в том, что для того, чтобы эти зада­ния обладали способностью дифференцировать испытуемых по уровню их подготовки, т.е. служить средством измерения этого уровня, их сложность должна соответствовать среднему уровню подготовки испытуемых в группе. Тест в целом должен включать в себя комплекс заданий различной сложно­сти - от достаточно простых до трудных, однако очевидно, что слишком простые задания, на которые правильно отвечают все до одного испытуемых, и слишком сложные задания, на которые не может ответить никто из испы­туемых, не обладают способностью дифференцировать их по уровню подго­товки и в этом смысле они не являются настоящими тестовыми заданиями. Такие задания должны «отбраковываться» и исключаться из теста.

Располагая упорядоченные значения индекса легкости (трудности) за­даний теста, как это представлено на рис. 46, можно оценить степень соот­ветствия составляющих тест заданий среднему уровню подготовки испыты­ваемой группы.

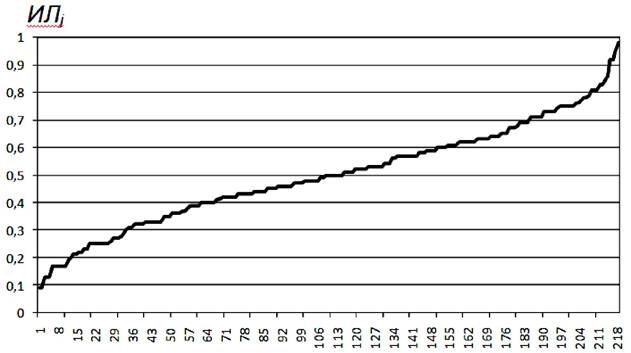
Рис. 46. Значения индекса лекости заданий для тестируемой группы

Представленные данные свидетельствует о том, что используемая в примере база тестовых заданий достаточно равномерно представляет вопро­сы различного уровня сложности, при этом очень легких - «очевидных для всех» и очень сложных - «никем не решаемых» (т.е. не тестовых заданий) практически нет, что говорит о соответствии комплекса заданий этого теста среднему уровню подготовки испытуемой группы.

Другой характеристикой, которую позволяют вычислять встроенные в систему Moodle средства анализа результатов тестовых заданий, является дисперсия of этих результатов (или их среднеквадратичное отклонение о). Дисперсия результатов выполнения тестовых заданий вычисляется по фор­муле:

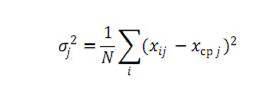
Дисперсия результатов of (или среднеквадратичное отклонение о) ха­рактеризует разброс баллов полученных всеми N испытуемыми при ответе на конкретное (/-е) задание теста. Если все испытуемые отвечают на задание одинаково, то характеризуемый этим параметром разброс полученных испы­туемыми баллов будет равен нулю. Нулевое или низкое значение разброса получаемых при выполнении конкретных тестовых заданий результатов в группе испытуемых свидетельствует о низкой дифференцирующей способ­ности этих заданий, т. е. их слабой способности разделять испытуемых в группе по степени их подготовки. Такие задания подлежат исключению из теста. Чем выше дифференцирующая способность тестовых заданий (больше величина разброса результатов), входящих в тест, тем выше качество теста.

На рисунке 47 приведен пример графика упорядоченных значений среднеквадратичного отклонения oj результатов тестирования, нормирован­ное на максимально возможное количество баллов х_{макс 7}, т. е. oJx_MaKCj, кото­рое можно получить за выполнением-го задания.

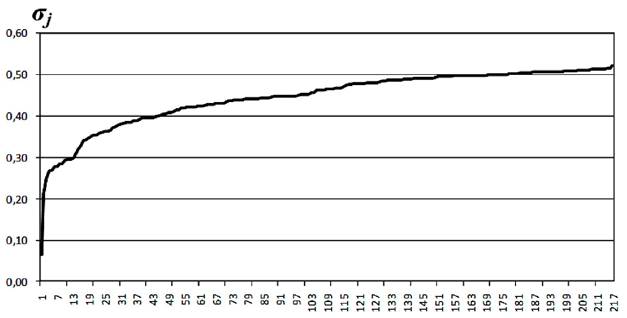
Рис. 47. Среднеквадратичное отклонение результатов выполнения заданий

Как видно из рис. 46, для большинства использованных в примере тес­товых заданий значение среднеквадратичное отклонение имеет значение больше 0,3, что в соответствии с требованиями педагогической теории изме­рений является хорошим показателем дифференцирующей способности тестовых заданий. Задания же, для которых это значение меньше 0,3, такой спо­собностью не обладают, и, поэтому, они должны исключаться из теста.

Еще одной важной статистической характеристикой качества тестовых заданий, которую позволяют вычислять средства Moodle, является коэффи­циент корреляции множества значений ответов, полученных испытуемыми при выполнении конкретного задания, с результатами выполнения этими же испытуемыми теста в целом, который рассчитывается по следующей формуле:

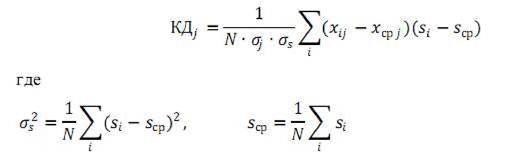
Os - дисперсия суммарных результатов испытуемых за выполнение всех заданий теста,

5_ср - среднее значение баллов, полученных всеми N испытуемыми за тест в целом,

Si - сумма баллов i-го испытуемого за выполнение всех заданий теста.

Этот показатель может принимать значения между -1 и +1 и в системе Moodle называется Коэффициентом Дифференциации (КД). Его использова­ние в качестве характеристики способности конкретного тестового задания правильно дифференцировать испытуемых по степени их подготовки, осно­вано на том, что в качественном тесте в среднем более высокие баллы при ответе на каждое конкретное задание теста должны получать испытуемые, набирающие более высокую сумму баллов за выполнение теста в целом. То есть, между этими значениями должна быть положительная корреляция. От­рицательные же значения этого коэффициента свидетельствует о том, что при ответе на данное задание более «слабые» испытуемые в среднем полу­чают более высокие баллы, чем более «сильные» испытуемые. Очевидно, что такие задания, возможно в силу допущенных ошибок в их формулировке или каких-либо иных причин, не являются настоящими тестовыми заданиями, и их также следует удалять из теста.

На рис. 47 приведен пример упорядоченных по величине значений ко­эффициента дифференциации, полученные для тех же тестовых заданий, что и в примерах на рис. 48 и 49.

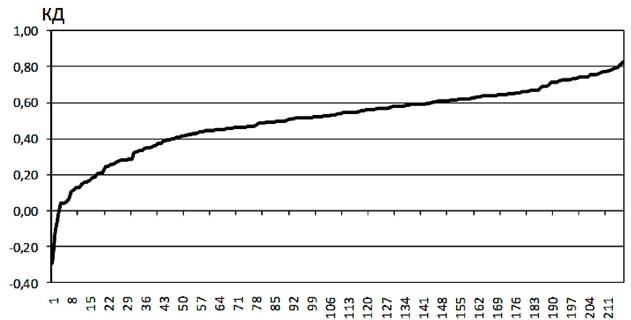
Рис. 48. Коэффициент дифференциации тестовых заданий

Cчитается приемлемым, если значение этого коэффициента превышает +0,3. Из приведенных в примере на рисунке 48 данных видно, что около 30-ти использованных в эксперименте тестовых заданий не удовлетворяют этим требованиям (КД < 0,3), более того, у нескольких заданий значения этого ко­эффициента имеют отрицательные значения, что свидетельствует об их яв­ных дефектах.

Встроенные в Moodle средства анализа позволяют также получать важ­ную статистическую информацию, позволяющую улучшать внутреннюю структуру тестового задания. В частности, для одного из часто используемо­го типа тестовых заданий, так называемых заданий в закрытой форме (выбор одного или нескольких правильных ответов из множества предлагаемых), можно получить данные, характеризующие эффективность работы каждого дистрактора такого тестового задания. Дистракторы (от англ. to distract - от влекать) это неправильные, но правдоподобные ответы, предлагаемые в за­даниях такого типа наряду с правильными ответами. Moodle позволяет опре­делять относительную частоту выбора испытуемыми тех или иных дистрак-торов при выполнении конкретного тестового задания. Очевидно, что дист-ракторы, которые выбираются редко или совсем не выбираются испытуемы­ми, являются неэффективными и, следовательно, должны быть изменены или удалены из списка дистракторов задания.

На рис. 48 представлен пример скриншота Moodle со статистическими характеристиками одного из тестовых заданий.

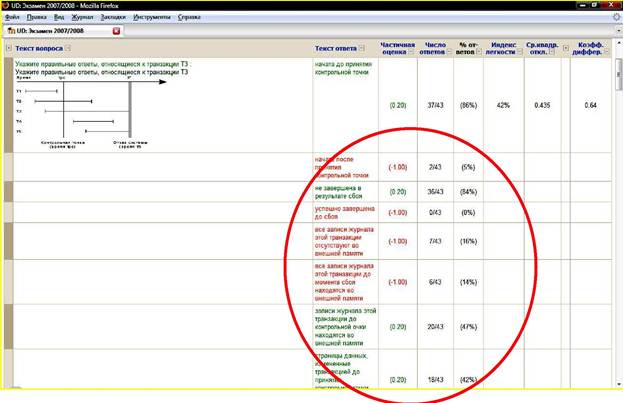
Рис. 49. Скриншот Moodle со статистическими характеристиками дистракторов тестового задания

Приведенные выше примеры показывают, что имеющиеся в системе Moodle средства не только дают возможность практической реализации ав­томатизированного контроля уровня подготовки обучаемых, но и предостав­ляют преподавателю эффективный механизм улучшения качества тестовых заданий и повышения точности и объективности оценки уровня испытуемых.

Возможность выявления не отвечающих необходимым требованиям заданий теста, а именно:

- слишком легких и слишком трудных заданий,

- заданий с малой дисперсией результатов,

- заданий с низким или отрицательным значением коэффициента диф­ференциации, не только позволяет улучшать качество теста за счет исключения из не­го таких проблемных заданий. Сам по себе анализ таких заданий, выяснение причин из-за которых они попали в «проблемную» группу, также обладает для разрабатывающего тест преподавателя большим методическим потен­циалом. Например, обнаружение того, что некоторое задание оказалось слишком трудным для группы испытуемых, может говорить не о дефекте са­мого задания, а о недостатках в проработке преподавателем на занятиях или в предлагаемых студентам учебно-методических методических материалах соответствующего раздела учебного курса. Анализ самих «проблемных» тес­товых заданий или их не эффективных дистракторов может побуждать к пере­работке формы и содержания таких заданий с целью устранения их дефектов.

Факторы, влияющие на погрешности измерения уровня подготовки обучаемых при использовании тестовых технологий

Говоря о влиянии качества тестовых заданий на способность теста служить средством для измерения уровня подготовки учащихся, следует иметь в виду, что на погрешности теста, как средства измерения, на практике могут значительно влиять внешние факторы, связанные с самой процедурой тестирования. Это, в первую очередь, факторы, связанные с нарушением принципа равенства требований и условий проведения тестирования для всех испытуемых.

Одним из таких факторов является угадывание испытуемыми результа­тов тестовых заданий. Для тестовых заданий, в особенности для заданий за­крытого вида (выбор одного или нескольких правильных ответов из конечно­го числа предлагаемых вариантов) существует ненулевая вероятность угадывания испытуемым правильных ответов при их случайном выборе. Очевидно, что чем больше такая вероятность, тем выше погрешность измерения при ис­пользовании теста, приводящая к дискриминации добросовестных испытуе­мых, то есть испытуемых, не прибегающих к угадыванию. В высказывается гипотеза о том, что чем ниже уровень знаний испытуемого, тем сильнее он мотивирован на угадывание, и для компенсации этого эффекта предлагается введение поправок на угадывание в исходный тестовый балл испытуемого.

В связи с этим, одной из важных задач, решаемых при составлении тес­тового задания, должно быть максимальное снижение вероятности угадыва­ния правильного ответа на него. Этим целям служит, в частности увеличение числа дистракторов в тестовых заданиях закрытого типа, так как, очевидно, что наибольшей уязвимостью в этом плане обладают тестовые задания с ма­лым числом дистракторов, в особенности задания с выбором одного пра­вильного ответа из двух предлагаемых, для которых вероятность угадывания составляет ½. Это является серьезным недостатком такого типа тестовых за­даний, вследствие которого их использование в тесте является крайне неже­лательным. Проблема, однако, состоит в том, что в целом ряде случаев спе­цифика предметной области конкретного тестового задания не позволяет выйти за рамки выбора одного из двух состояний. Например, в случае про­верки знания испытуемым функционирования цифровых логических схем, сигналы на входах и выходах которых принципиально могут находиться в одном из двух состояний - 0 или 1 (true или false). В таких случаях, можно рекомендовать объединение в одном тестовом задании нескольких вопросов с выбором одного из двух состояний. Система Moodle позволяет строить та­кого рода усложненные задания, пример которого приводится на рис. 50.

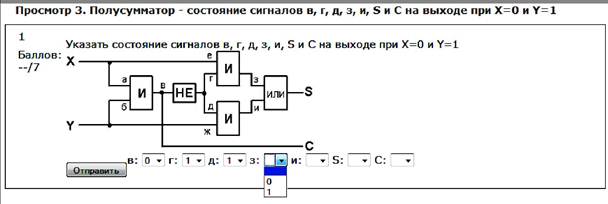
Рис. 50. Пример объединения в одном тестовом задании нескольких вопросов с выбором одного из двух состояний

Большие возможности с точки зрения составления тестовых заданий с низкой возможностью угадывания правильных ответов в системе Moodle предоставляет тип задания, называемый Вложенные ответы, позволяющий объединять в одном задании вопросы с ответами разных типов. Задания типа Вложенные ответы состоят из текста, непосредственно в который вставля­ются ответы на вложенные в этот текст вопросы типов - Множественный выбор, Короткие ответы и Числовые (рис. 51).

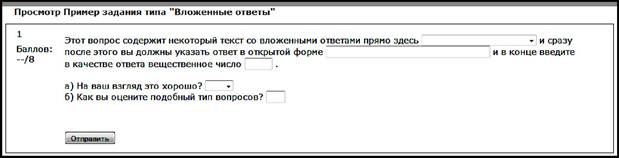
Рис. 51. Пример тестового задания типа Вложенные ответы

Другим практически значимым фактором, нарушающим принцип ра­венства требований и условий проведения тестирования для всех испытуе­мых, является возможность получения испытуемыми во время прохождения тестирования доступа к правильным ответам на задания теста. Каналами та­кого доступа могут быть подсказки других испытуемых, подсматривание от­ветов у соседа, использование шпаргалок, а сейчас и использование сторонней дистанционной помощи с применением современных технических средств компьютерной и мобильной связи.

Для противодействия возможностям такой компрометации процедуры тестирования используется целый ряд известных средств.

Во-первых, это использование в тестовых заданиях типа Множествен­ный выбор опции случайного перемешивания ответов при каждом предъяв­лении задания испытуемым. Это устраняет связывание правильных ответов с порядковым номером предъявляемых ответов, исключая использование по­рядкового номера правильных ответов при составлении шпаргалок и списы­вании.

Опыт использования тестовых технологий показывает, что при форми­ровании набора тестовых заданий составляющих тест, предназначенный для многократного использования для разных тестируемых, является совершенно не оправданным предположение о том, что используемый в тесте фиксиро­ванный набор заданий может оставаться неизвестным и неожиданным для испытуемых сколько-нибудь продолжительное время. Для обеспечения дей­ствительно надежного фактора новизны предлагаемого конкретному испы­туемому набора тестовых заданий наиболее эффективным является форми­рование сценария теста путем случайного выбора каждого конкретного тес­тового задания из множества однотипных заданий однородных по уровню сложности. Такое формирование тестов может быть обеспечено только при наличии достаточно большого исходного банка тестовых заданий по каждо­му разделу учебной дисциплины, по которой осуществляется контроль зна­ний испытуемых.

При этом следует, однако, учитывать следующее обстоятельство. Выше были рассмотрены показатели тестовых заданий - мера трудности задания, вариация результатов его выполнения в группе испытуемых, его дифферен­цирующая способность, характеризующие качество тестового задания, как средства измерения уровня подготовки испытуемого. Важно иметь в виду, что эти показатели являются статистическими величинами, получаемыми путем усреднения по выборке выполняющих их испытуемых, и, следовательно, обеспечение точности их экспериментального определения принципиально требует их апробации на возможно большем количестве испытуемых. При этом, однако, оказывается, что это требование вступает в противоречие с не­обходимостью практического формирования сценария тестирования путем случайного выбора предъявляемых конкретному испытуемому тестовых за­даний из более или менее обширного банка заданий, целью которого являет­ся снижение вероятности включения одних и тех же тестовых заданий в раз­ных сеансах тестирования по одному и тому же тесту. Очевидно, что в этом случае, даже при большом общем количестве реально участвующих в тести­ровании испытуемых, количество испытуемых, которым реально достанутся одинаковые тестовые задания, будет существенно ниже, что неизбежно сни­жает надежность вычисляемых показателей качества тестовых заданий при их анализе. Это противоречие обязательно следует учитывать как при фор­мировании сценариев тестирования, так и при интерпретации автоматически рассчитываемых системой статистических показателей качества тестовых за­даний для поиска необходимого компромисса.