
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания

Прикладные задачи динамики ледяного покрова
Козин В. М., Жесткая В. Д., Погорелова А. В., Чижиумов С. Д., Джабраилов М. Р., Морозов В. С., Кустов А. Н.,
5.2. Определение коэффициента погонной жесткости упругого шарнира при моделировании трещины
Величина коэффициента пропорциональности kможет быть определена экспериментально из натурных экспериментов по изгибу ледяной балки прямоугольного поперечного сечения с разрезом по середине, опертой по краям и нагруженной внешней нагрузкой, вызывающей поворот смежных частей балки относительно друг друга. Выполнение таких экспериментов - крайне сложная задача, сопряженная с целым рядом трудно разрешимых проблем. Они связаны со спецификой льда, как природного материала, а также с необходимостью соблюдения температурного режима в лабораторных условиях, либо с необходимостью проведения экспериментов в тяжелых полевых условиях. Поэтому, с помощью средств математического моделирования натурный эксперимент был заменен “виртуальным”.
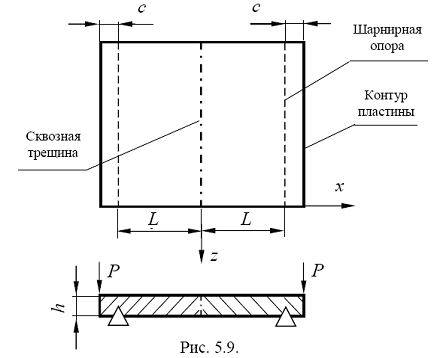
Для определения коэффициента kрассмотрим прямоугольную в плане пластину толщиной h произвольной ширины, длина которой равна ![]() (рис. 5.9). Введем систему координат, совместив оси xи zсо срединной плоскостью пластины так, что осьxнаправлена вдоль одной из свободных сторон пластины, ось y- перпендикулярно плоскости пластины вертикально вверх, а ось z- вдоль линии трещины.
(рис. 5.9). Введем систему координат, совместив оси xи zсо срединной плоскостью пластины так, что осьxнаправлена вдоль одной из свободных сторон пластины, ось y- перпендикулярно плоскости пластины вертикально вверх, а ось z- вдоль линии трещины.
Пластина делится прямой сквозной трещиной, параллельной шарнирно опертым сторонам, на две половины длиной ![]() каждая (см. рис. 5.9). Две стороны пластины, параллельные оси z, шарнирно оперты, причем опоры расположены на прямых x = ± L, а две другие, параллельные оси x, свободны. Изгиб пластины вызывается моментом, создаваемым нагрузкой P, равномерно распределенной по краям пластины, параллельным оси z. Ввиду плоской симметрии задачи относительно осиz достаточно рассмотреть сечение пластины в виде двухпролетной балки-стенки (рис. 5.10, а) толщиной
каждая (см. рис. 5.9). Две стороны пластины, параллельные оси z, шарнирно оперты, причем опоры расположены на прямых x = ± L, а две другие, параллельные оси x, свободны. Изгиб пластины вызывается моментом, создаваемым нагрузкой P, равномерно распределенной по краям пластины, параллельным оси z. Ввиду плоской симметрии задачи относительно осиz достаточно рассмотреть сечение пластины в виде двухпролетной балки-стенки (рис. 5.10, а) толщиной ![]() (
(![]() - размер балки-стенки в направлении, перпендикулярном плоскости сечения).
- размер балки-стенки в направлении, перпендикулярном плоскости сечения).
 .
.
 .
.
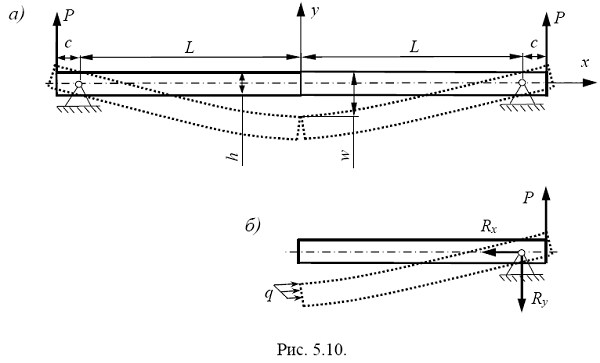
При данном закреплении и нагрузке, для такой балки-стенки имеет место симметрия относительно плоскости сечения с трещиной, поэтому достаточно рассчитывать только один пролет балки-стенки, например, справа от трещины, наложив соответствующие ограничения на перемещения для точек балки-стенки, лежащих в плоскости симметрии (рис. 5.10, б). Таким ограничением является запрет на перемещения точек контактного сечения правой части балки-стенки левее плоскости симметрии.
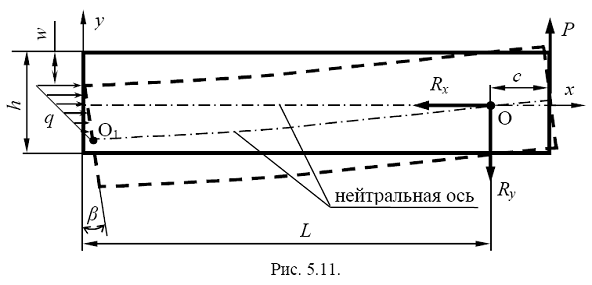
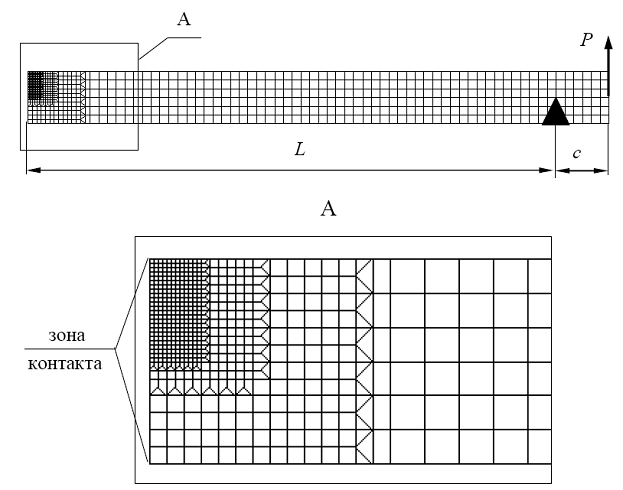
В программном комплексе конечноэлементного анализа MSC/Nastran был выполнен расчет одного пролета балки-стенки в нелинейной постановке с моделированием контакта. Балка-стенка моделировалась плоскими мембранными элементами единичной толщины, допускающими перемещения только в своей плоскости (плоская деформация). Расчетная схема приведена на рис. 5.11. Схема разбивки балки-стенки на конечные элементы приведена на рис. 5.12. В зоне контакта использовались квадратные конечные элементы с длиной стороны равной 2 см, что составляет 2 % от высоты балки-стенки (толщины льда). Использование конечных элементов в зоне контакта с длиной стороны равной 1 см (1 % от высоты балки-стенки) дало практически идентичный результат, поэтому в расчетах использовалась сетка с более крупным размером элементов. В регулярной зоне использовались квадратные конечные элементы, длина сторон которых определялась из условия, чтобы по высоте балки-стенки размещалось шесть элементов. Конечным элементам дискретной модели был выбран материал пластины, который считался изотропным и имел следующие параметры: модуль Юнга E = 0,73?1010 Па; коэффициент Пуассона ν = 0,3.
 .
.
Нагружение осуществлялось сосредоточенной силой P, прикладываемой на некотором расстоянии c от опоры. Для определённости расстояние c можно принять равным высоте балки-стенки. Сила P и реакция опоры ![]() вызывают действие момента пары сил, который стремится повернуть балку-стенку вокруг шарнирной опоры. В расчетной схеме приведены обозначения: h– ширина балки-стенки (толщина пластины); w– перемещения (прогиб) в месте трещины;
вызывают действие момента пары сил, который стремится повернуть балку-стенку вокруг шарнирной опоры. В расчетной схеме приведены обозначения: h– ширина балки-стенки (толщина пластины); w– перемещения (прогиб) в месте трещины;![]() ,
, ![]() – реакции в шарнирной опоре; q - распределенное контактное усилие.
– реакции в шарнирной опоре; q - распределенное контактное усилие.
 .
.
Рис. 5.12. Схема конечноэлементной модели балки-стенки
Внешняя нагрузка P и реакции шарнирной опоры O (рис. 5.11) создают в точке контактного сечения O1, лежащей на нейтральной линии балки-стенки, изгибающий момент M, который уравновешивается моментом, создаваемым распределённым контактным усилием q относительно этой же точки. Величина действующего в контактном сечении погонного момента M, определяется по формуле:
![]() , (5.10)
, (5.10)
где δ - толщина балки-стенки.
При приложении нагрузки контактное сечение балки-полоски поворачивается на угол ![]() . Симметричная часть балки-стенки поворачивается в противоположную сторону на такой же угол, поэтому угол раскрытия берегов трещины составлял
. Симметричная часть балки-стенки поворачивается в противоположную сторону на такой же угол, поэтому угол раскрытия берегов трещины составлял ![]() .
.
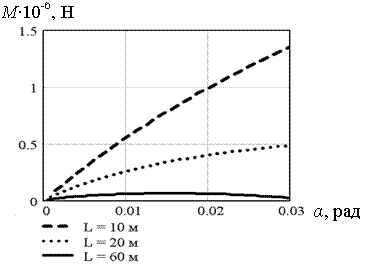
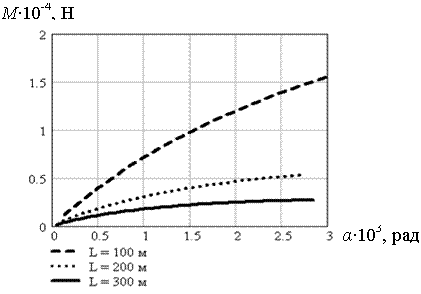
По вышеизложенной схеме были проведены серии расчетов для льда толщиной 0,2; 0,5; 0,7; 1,0 м. При h = 0,2 м рассчитывались балки-стенки с длиной пролета L = 10, 20, 30, 40, 50 м. При h = 0,5 м - с длиной пролета L = 10, 20, 30, 40, 50, 60 м. При h = 0,7 м - с длиной пролета L = 10, 20, 30, 40, 50, 60, 70 м. При h = 1,0 м - с длиной пролета L = 10, 20, 60, 100, 200, 300 м. Дискретные модели балок-стенок для каждой из рассматриваемых толщин льда составлялись из квадратных конечных элементов (за исключением переходных зон) согласно правилу: в регулярных областях размер конечных элементов равнялся 1/6, а в зоне контакта – 1/48 высоты балки-стенки. В результате расчетов получены графики зависимости величины погонного изгибающего момента , действующего в контактном сечении, от угла раскрытия сквозной трещины. При h = 1,0 м данные зависимости для длины пролета L = 10, 20, 60 м представлены на рис. 5.13, а для L = 100, 200, 300 м - на рис. 5.14. Аналогичные зависимости получены и для остальных рассмотренных толщин льда. Как видно из графиков, зависимость изгибающего момента от угла раскрытия нелинейная. Однако при малых прогибах и, следовательно, малых углах раскрытия сквозной трещины эту зависимость приближенно можно считать линейной с допустимой долей погрешности. В этом случае коэффициент пропорциональности между погонным изгибающим моментом и углом раскрытия сквозной трещины равен тангенсу угла наклона касательной к графику с осью абсцисс и его можно рассчитать по формуле:
![]() . (5.11)
. (5.11)
Допустимые значения углов раскрытия берегов трещины, при которых погрешность линеаризации зависимости изгибающего момента M от угла α не превышает 5-6 %, приведены в таблице 5.1.
 .
.
Рис. 5.13. Зависимость погонного изгибающего момента M от угла раскрытия берегов трещины α при толщине льда h = 1 м (L = 10, 20, 60 м)
Характер напряженного состояния балки-стенки в зоне контакта проиллюстрирован рисунками 5.15-5.18, на которых представлено распределение нормальных σx , σy , касательных τxy и эквивалентных σэкв напряжений в данной зоне для случая h = 1,0 м, L = 20 в момент нагружения, когда величина прогиба в контактном сечении составила 0,243 м. Эквивалентные напряжения рассчитывались по формуле:
![]() . (5.12)
. (5.12)
 .
.
Рис. 5.14. Зависимость погонного изгибающего момента M от угла раскрытия берегов трещины α при толщине льда h = 1 м (L = 100, 200, 300 м)
Таблица 5.1.
Максимальные углы раскрытия трещины, при которых погрешность линеаризации момента M не превышает 5-6 %
| α·103, рад | ||||
| h, м L, м | 0,2 | 0,5 | 0,7 | 1,0 |
| 10 | 1,167 | 3,368 | 4,710 | 7,493 |
| 20 | 0,539 | 1,505 | 2,084 | 3,668 |
| 30 | 0,336 | 1,022 | 1,244 | - |
| 40 | 0,236 | 0,754 | 0,900 | - |
| 50 | 0,175 | 0,512 | 0,680 | - |
| 60 | - | 0,436 | 0,578 | 1,179 |
| 70 | - | - | 0,525 | - |
| 100 | - | - | - | 0,513 |
| 200 | - | - | - | 0,223 |
| 300 | - | - | - | 0,165 |
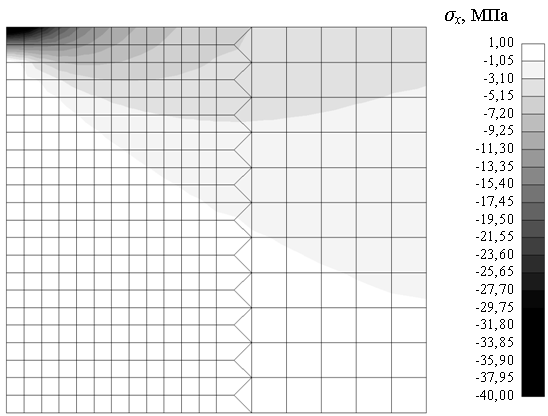
Рис. 5.15. Распределение нормальных напряжений σx в зоне контакта

Рис. 5.16. Распределение нормальных напряжений σy в зоне контакта

Рис. 5.17. Распределение касательных напряжений τxy в зоне контакта

Рис. 5.18. Эквивалентные напряжения σэкв в зоне контакта
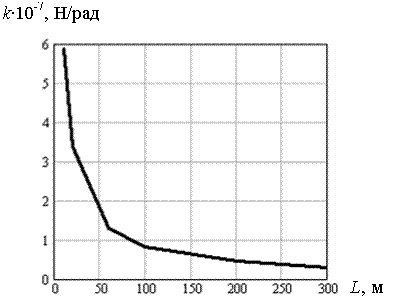
Рис. 5.19. Зависимость коэффициента погонной жесткости k от длины пролета L балки-стенки при толщине льда h = 1 м
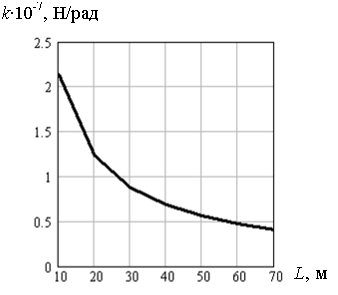
Рис. 5.20. Зависимость коэффициента погонной жесткости k от длины пролета L балки-стенки при толщине льда h = 0,7 м
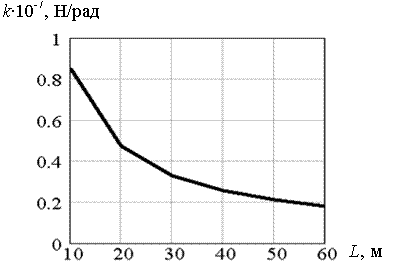
Рис. 5.21. Зависимость коэффициента погонной жесткости k от длины пролета L балки-стенки при толщине льда h = 0,5 м
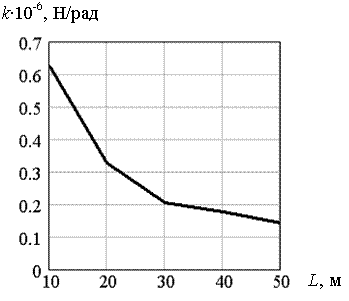
Рис. 5.22. Зависимость коэффициента погонной жесткости k от длины пролета L балки-стенки при толщине льда h = 0,2 м
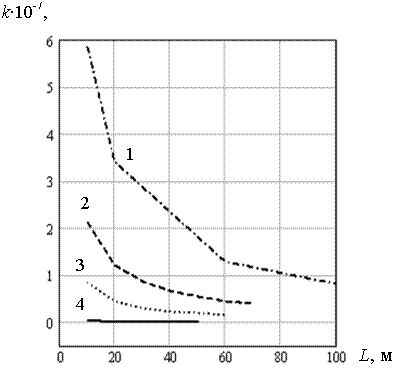
Рис. 5.23. Зависимость коэффициента погонной жесткости k от длины пролета L балки-стенки при толщинах льда h равных 1,0; 0,7; 0,5; 0,2 м. (кривые 1, 2, 3, 4 - соответственно)
На рисунках 5.19-5.22 представлены графики зависимости коэффициента погонной жесткости k от длины пролета L балки-стенки шириной h = 1; 0,7; 0,5; 0,2 м. Данные графики объединены на рис. 5.23, который дает наглядное представление о влиянии толщины льда на величину коэффициента погонной жесткости k. Видно, что с увеличением толщины льда значения коэффициента k довольно быстро возрастают.