
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
Монографии, изданные в издательстве Российской Академии Естествознания
1.1. Основные зависимости задачи
В качестве основных зависимостей, моделирующих задачу, примем дифференциальное уравнение вязкоупругих колебаний ледяного покрова [1]
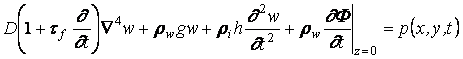 , (1.1)
, (1.1)
уравнение Лапласа для потенциала скорости движения жидкости
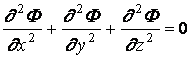 , (1.2)
, (1.2)
граничные условия на дне водоема и на границе льда и воды
 , (1.3)
, (1.3)
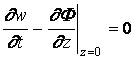 , (1.4)
, (1.4)
где w - прогиб льда, t – время, rw - плотность воды, ri - плотность льда, g - ускорение свободного падения, h - толщина льда, F - потенциал скорости движения жидкости, p - интенсивность внешней нагрузки, H - глубина водоема, tf - время релаксации деформаций, D - цилиндрическая жесткость пластины.
Оси x и y лежат в плоскости ледяной пластины, ось z направлена вверх (рис.1.1).
