
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
1.3. Система матричных дифференциальных уравнений задачи
Используя алгоритм метода конечных элементов, построим дискретную модель ледяной пластины и положим, что
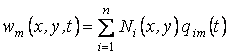 , (1.11)
, (1.11)
где Ni(x,y) - функции формы, qim(t) - компоненты вектора узловых перемещений [q]m(t):
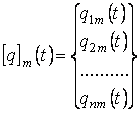 , (1.12)
, (1.12)
n - число узловых перемещений, оно же – число степеней свободы дискретной модели, поскольку перемещения в любой точке дискретной модели полностью определяются набором узловых перемещений. Тот же смысл эта величина имеет и в формулах (1.5), (1.6). Значение n связано с типом и количеством конечных элементов, образующих дискретную модель ледяной пластины. Необходимое для достижения достаточной точности число конечных элементов оценивается отдельно для каждой конкретной задачи.
Прогиб пластины
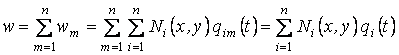 ,
,
где
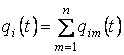 .
.
Величины qi(t) являются компонентами полного вектора узловых перемещений [q](t):
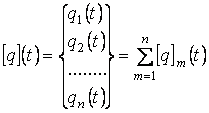 . (1.13)
. (1.13)
Для получения разрешающей системы уравнений задачи применим обобщенный метод Бубнова-Галеркина.
Из первого уравнения системы (1.10), интегрируя по площади пластины S, получим
 .
.
и затем
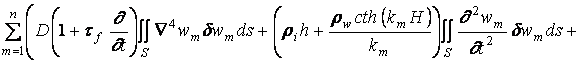 .
.
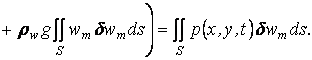 (1.14)
(1.14)
Интеграл ![]() входящий в (1.14), можно привести к виду
входящий в (1.14), можно привести к виду
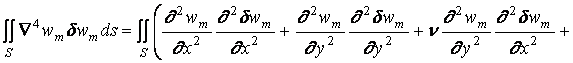 .
.
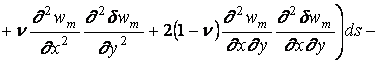 .
.
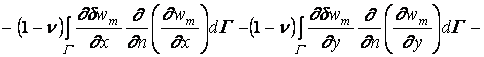 .
.
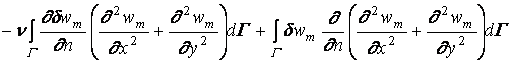 ,(1.15)
,(1.15)
где Г - граница области S, ![]() - производная по нормали к Г.
- производная по нормали к Г.
В ряде случаев вместо (1.15) можно использовать аналогичную, но более простую зависимость:
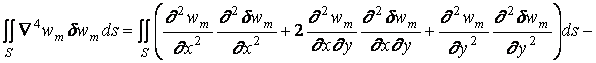 .
.
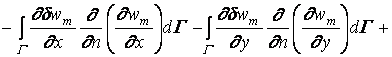 .
.
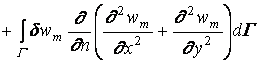 . (1.16)
. (1.16)
Укажем некоторые типы граничных условий, приводящих к нулевому значению интегралов по контуру в (1.15), (1.16) [2]. Во всех случаях рассматривается прямоугольная пластина; оси x и y совмещены с ее продольной и поперечной кромками.
1. Пластина жестко заделана по контуру.
2. Одна из продольных кромок (y = b) пластины совершенно свободна, остальные кромки жестко заделаны.
3. Одна из поперечных кромок (x = a) совершенно свободна, остальные - жестко заделаны.
Если интегралы по контуру Г в (1.16) равны нулю, то (1.14) принимает вид
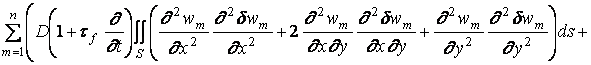 .
.
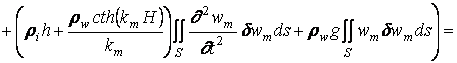 .
.
![]() . (1.17)
. (1.17)
На основании (1.11) вариация перемещения wm
![]() .
.
Внося wm в форме (1.11) и dwm в (1.17) и сокращая на dqjm , получим:
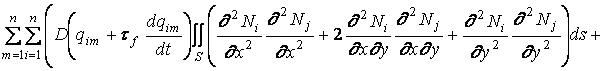 .
.
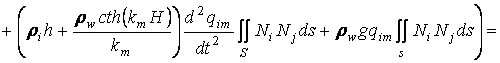 .
.
![]() , j=1,2,....,n . (1.18)
, j=1,2,....,n . (1.18)
Обозначим
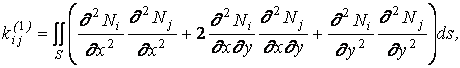 (1.19)
(1.19)
![]() (1.20)
(1.20)
В случае использования формулы (1.15) получим вместо (1.19)
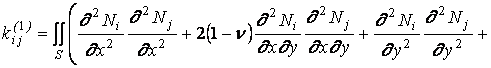 .
.
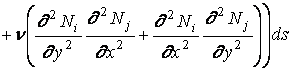 . (1.21)
. (1.21)
С учетом обозначений (1.19), (1.20), (1.21) формула (1.18) примет вид
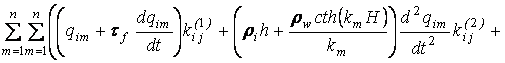 .
.
![]() (1.22)
(1.22)
Полученную систему уравнений (1.22) можно записать в виде матричного уравнения
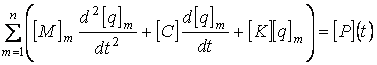 , (1.23)
, (1.23)
где элементы mi j матрицы [M]m находятся по формуле
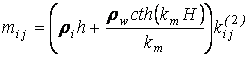 ,
,
элементы ci j матрицы [C] - по формуле
![]() ,
,
элементы ki j матрицы [K] - по формуле
![]() ,
,
а [P](t) - вектор внешних узловых нагрузок, компоненты которого определяются следующим образом:
![]() .
.
Рассмотрим теперь второе уравнение системы (1.10). Принимая в качестве весовой функции величину 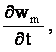 пропорциональную jm (см. уравнение (1.9)), согласно методу Бубнова-Галеркина можем написать, что
пропорциональную jm (см. уравнение (1.9)), согласно методу Бубнова-Галеркина можем написать, что
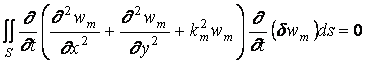 . (1.24)
. (1.24)
Это выражение, интегрируя по частям и учитывая граничное условие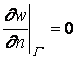 , можно привести к виду
, можно привести к виду
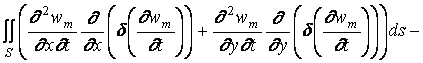 .
.
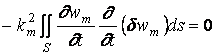 . (1.25)
. (1.25)
Подставив в (1.25) wm в форме (1.11) и dwm = Nj(x,y)dqjm(t), после сокращения на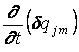 получим
получим
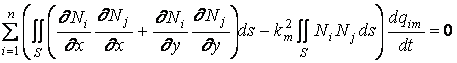 . (1.26)
. (1.26)
Вводя обозначение
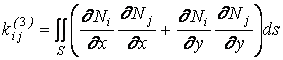 , (1.27)
, (1.27)
перепишем (1.26) в виде
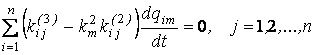 .
.
Полученную систему уравнений представим в матричной форме:
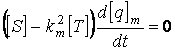 , (1.28)
, (1.28)
где ![]() .
.
Таким образом, исходные зависимости задачи с помощью МКЭ сведены к системе двух матричных уравнений (1.23) и (1.28):
 (1.29)
(1.29)
