Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Численный расчет напряженно-деформированного состояния ледяного покрова, находящегося под действием нестационарной нагрузки

Жесткая В. Д., Чижиумов С. Д.,

3.3. Расчет напряженно-деформированного состояния ледяного покрова при действии на него движущейся распределенной нагрузки

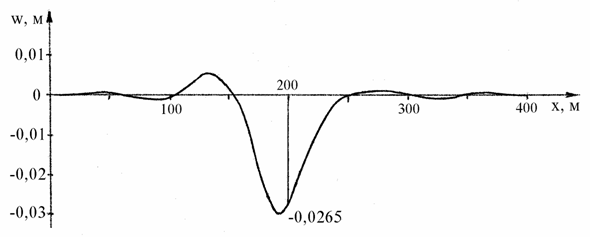
Рассматривается движение по ледяной пластине прямоугольной в плане равномерно распределенной нагрузки. Точка приложения еe равнодействующей перемещается по такому же закону, как сила Р в задаче 1 (п. 3.1.1), параметры задачи имеют те же значения. Нагрузка считается распределенной по прямоугольной области, стороны которой d_x и d_y параллельны осям координат. Дискретизация пластины, область приложения нагрузки и нумерация узлов показаны на рис. 3.16. Расчет был выполнен при d_x = 15 м, d_y = 7 м  с учетом симметрии ледяной пластины и нагрузки. На рис. 3.17 дан построенный по результатам счета график прогибов в точках, лежащих на оси x, в момент прохождения центра распределенной нагрузки через узел 7.

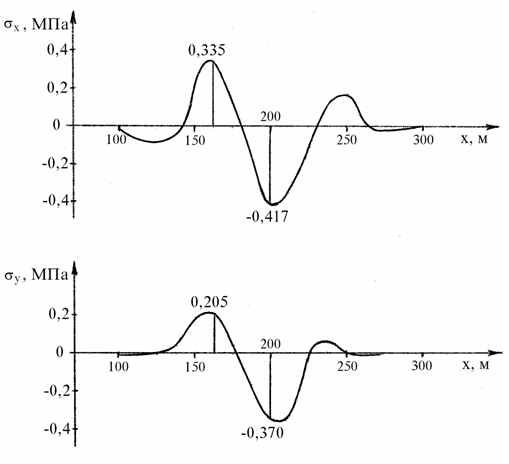
Для того же момента времени на рис. 3.18 показаны эпюры напряжений  в точках заштрихованной на рис. 3.16 области ледяной пластины, лежащих на оси x.

Сравнивая результаты решения этой задачи и задачи 1 (п. 3.1), можно заметить, что они практически повторяют друг друга. Картина прогибов ледяной пластины в обоих случаях одна и та же, значения прогибов и напряжений очень близки, что видно, например, из сравнения рис. 3.17 и соответствующего графика на рис.3.3, а также из сравнения эпюр напряжений на рис. 3.4, 3.5, 3.18. Таким образом, замена распределенной нагрузки ее равнодействующей в данном случае почти не сказывается на полученных расчетом параметрах напряженно-деформированного состояния.

 .

 .

Рис. 3.17. Прогибы в точках пластины, лежащих на оси x, при прохождении центра распределенной нагрузки через узел 7.

Отметим, что в исходных данных задачи о движении по льду распределенной нагрузки, рассмотренной в настоящей главе, площадь 15´7 м², занятая нагрузкой, примерно соответствует размерениям СВП, имеющего вес, приблизительно равный 0,4×10⁶ H, то есть значению силы Р (задача 1, п. 3.1) или равнодействующей распределенной нагрузки. Таким образом, при решении задачи о движении по льду СВП, имеющего такой вес и размерения, вполне допустимо представлять его как сосредоточенную силу, равную его весу.

 .

Рис. 3.18. Эпюры напряжений в точках пластины, лежащих на оси x, при прохождении центра распределенной нагрузки через узел 7.