
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
3.1.3. Задача 3. Внезапное приложение силы
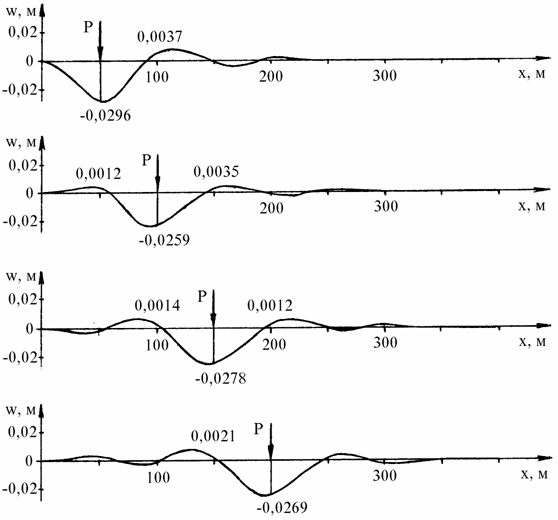
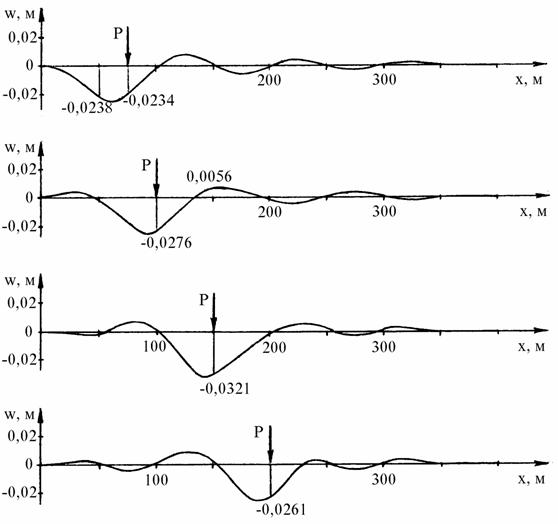
Сила Р внезапно приложена в точке А (см.рис. 3.1) и имеет при этом горизонтальную скорость v (ситуация напоминает посадку самолета на лед). В этом случае входящий в исходные данные параметр met1 был принят равным 1, то есть при t = 0 узловые перемещения и скорости движения точек пластины считались равными нулю. Остальные параметры задачи были такими же, как в задаче 2. Построенные по рассчитанным значениям узловых перемещений графики прогибов точек оси x для четырех моментов времени даны на рис. 3.10 (соответствующие положения силы Р обозначены стрелкой).
 .
.
Рис. 3.9. Графики прогибов ледяной пластины (задача 2).
Приведенные задачи показывают, что алгоритм, изложенный в гл. 1, правильно отражает физическую сущность явлений, возникающих при движении нагрузки по ледяному покрову, и позволяет получить достаточно верную картину процесса. В частности, на примерах задач 1 и 2 видно, что при прямолинейном движении силы с постоянной скоростью состояние ледяного покрова выглядит так, как будто установившаяся картина прогибов скользит вместе с силой Р в направлении движения последней. Такой эффект был отмечен на практике, при наблюдении за движением реального СВП. Рассматривая результаты решения задачи 3, можно заметить, что в начальной стадии движения нагрузки существенно влияние реакции упругого основания (прогибы в данном случае меньше, чем при статическом нагружении). Более высокие значения прогибов, чем в задачах 1 и 2, объясняются интерференцией волн (внезапно приложенная нагрузка возбуждает кольцевые расходящиеся волны, которые накладываются на волны, образующиеся при последующем поступательном движении силы). Затем процесс стабилизируется и картина прогибов льда становится такой же, как и тогда, когда нагрузка начинает движение из состояния покоя.
 .
.
Рис. 3.10. Графики прогибов ледяной пластины (задача 3).
