Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Численный расчет напряженно-деформированного состояния ледяного покрова, находящегося под действием нестационарной нагрузки

Жесткая В. Д., Чижиумов С. Д.,

4.1. Расчет резонансных значений скорости, максимальных прогибов и напряжений в ледяном покрове при решении задачи в динамической постановке

Наблюдалось на практике и упомянуто во многих научных публикациях ([1] и др.) появление пика прогибов ледяного поля при достижении перемещающейся нагрузкой некоторой скорости v_p. За этим  явлением в специальной литературе, посвященной этому вопросу, закрепилось название “резонанс”, а скорость v_р обычно называют резонансной, или критической.

Явление резонанса можно объяснить следующим образом. При скорости v, меньшей v_р, интенсивность реакции воды по знаку такая же, как в случае статического действия нагрузки. По мере приближения v к v_р взаимодействие изгибной волны в ледяной пластине и гравитационной волны в воде становится таким, что реакция воды уменьшается; она может не только обратиться в нуль, но и изменить знак [6]. Таким образом, вода перестает поддерживать ледяной покров; внутренние силы упругости в ледяной пластине должны уравновесить не только внешнюю нагрузку, но и добавочное давление, создаваемое инерцией воды, что и приводит к появлению пика прогибов ледяного покрова при v = v_р.

 Исследовать зависимость максимальных значений прогиба и напряжений в ледяном поле от скорости движения нагрузки можно, используя численный метод расчета, изложенный в гл. 2.  В качестве примера такого исследования рассмотрим следующую задачу.

Пусть из ледяного покрова выделена прямоугольная в плане пластина длиной L = 1200 м и шириной B = 200 м (рис.4.1). Такие размеры достаточны для того, чтобы принять на кромках пластины условия жесткой заделки.

По оси симметрии пластины x движется сосредоточенная сила P. До начала движения она находилась в покое в точке x = 50 м, y = 0; при этом ледяная пластина имела соответствующий статический прогиб. Начав двигаться по прямой y = 0 и набрав скорость v, сила продолжает дальнейшее  движение в том же направлении, т.е. по оси x, с постоянной скоростью.

 .

Примем следующие значения параметров задачи: P = 0,4×10⁶ Н; E = 0,73×10¹⁰ Пa, что примерно соответствует середине известного диапазона значений модуля Юнга льда; коэффициент Пуассона n = 0,3;  плотность льда r_i = 900 кг/м³; плотность воды r_w = 1000 кг/м³; глубина водоема H = 5 м; время релаксации деформаций t_f  = 10 с. При расчетах варьировались скорость движения нагрузки v и толщина ледяного покрова h. Дискретная модель пластины образована квадратными конечными элементами со стороной а = 50 м.

Напряжения и прогибы определялись при установившемся напряженно-деформированном состоянии, т.е. для того периода времени, когда установившаяся картина деформаций ледяного поля как бы скользит вместе с силой Р в направлении движения последней, оставаясь неизменной для наблюдателя, перемещающегося вместе с Р. На этой стадии движения особенности периода разгона нагрузки от нулевой скорости до ее конечного значения уже перестают сказываться на характере напряженно-деформированного состояния, поэтому время разгона t₀ было принято равным нулю. Шаг сетки времени Dt был принят равным 0,3125 с. Статический прогиб ледяной пластины в момент начала движения нагрузки, который также входит в число исходных данных при решении задачи, определялся автоматически в начале  работы программы расчета. При расчете учтена симметрия пластины относительно оси x.

При решении задачи было рассмотрено пять значений h:  0,3; 0,4; 0,5; 0,75; 1,0 м. Границы диапазона толщин были приняты из следующих соображений. Практика показала, что разрушение льда толщиной более 1 м резонансным методом с помощью СВП становится уже проблематичным, так что с этой точки зрения здесь целесообразно ограничиться именно этим значением h. С другой стороны, при расчете НДС ледяной пластины сравнительно малой толщины (менее 0,3 м) может оказаться существенным влияние цепных напряжений, которые в данной методике не учитываются.

Что касается принятого значения глубины водоема H, то исследование НДС ледяного покрова при действии на последний движущейся нагрузки в условиях мелководья представляет большой интерес, так как именно на мелкой воде наиболее эффективно, а иногда и единственно возможно, использование для разрушения льда СВП.

Расчет выполнялся в следующем порядке. При некоторых выбранных значениях скорости производилось вычисление прогибов для ряда достаточно близких друг к другу моментов времени на протяжении всего периода перемещения нагрузки от начала движения до достижения ею конца пластины. На основании этого расчета определялось, в какой период времени или, другими словами, начиная и кончая какими значениями абсциссы точки приложения силы Р при перемещении ее в пределах принятой длины ледяного поля, процесс можно считать установившимся. После этого выполнялся расчет напряжений и прогибов при выбранной скорости и при нескольких меньших значениях v. Например, найдя, что при скорости v = 6,4 м/с процесс уже является установившимся в момент, когда Р проходит точку x = 650 м, можно тем более утверждать, что он в этой точке будет таковым и при v = 6 м/с, и при v = 5 м/с, и произвести расчет прогибов и напряжений при этих скоростях без какой-либо дополнительной проверки этого обстоятельства.

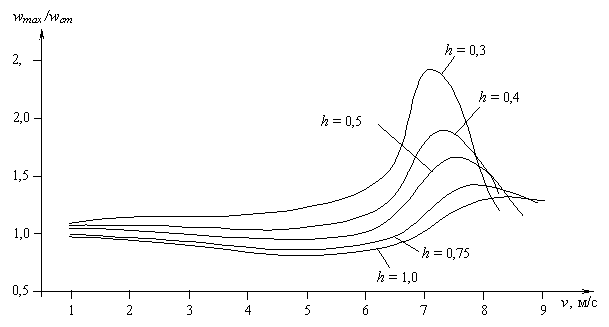
На рис. 4.2 - 4.4 представлены в графической форме результаты расчетов прогибов и напряжений. На графиках даны относительные максимальные прогибы и относительные нормальные напряжения. Под относительным прогибом понимается отношение w_max / w_ст , где w_max - максимальный динамический прогиб, а w_ст - максимальный прогиб, возникающий при данной толщине ледяного покрова в случае статического приложения силы Р в центре рассматриваемой ледяной пластины. Аналогично, полученные расчетом максимальные значения нормальных напряжений s_{x max} и s_{y max} отнесены к максимальным напряжениям s_{x ст} , s_{y ст} , определенным  при указанном выше статическом приложении силы. В качестве приближенных значений максимальных напряжений  принимались полученные при расчете наибольшие значения s_x  , s_y  в пределах того конечного элемента, где возникают наибольшие деформации.

 .

 Рис. 4.2. График зависимости w_max / w_ст от скорости v при глубине водоема H =5 м.

 .

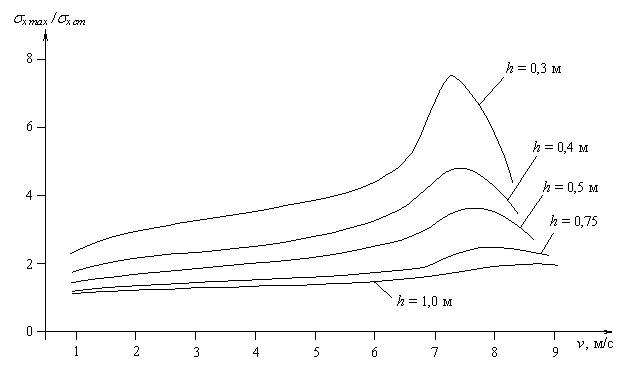
Рис. 4.3. График зависимости  s_{x max} / s_{x ст}  от скорости v при глубине водоема H = 5 м.

По результатам расчетов можно сделать следующие выводы.

1. Значение резонансной скорости зависит, во-первых, от глубины водоема H и, во-вторых, также и от толщины ледяного покрова. На графике зависимости w_max / w_ст от скорости v при H = 5 м (рис. 4.2) хорошо видно, как максимум относительного прогиба смещается в сторону бóльших значений v при увеличении толщины льда h. В рассмотренном диапазоне h при малых толщинах скорость v_р, соответствующая максимуму прогиба (резонансная скорость), близка к фазовой скорости гравитационной волны в воде, немного превосходя последнюю.

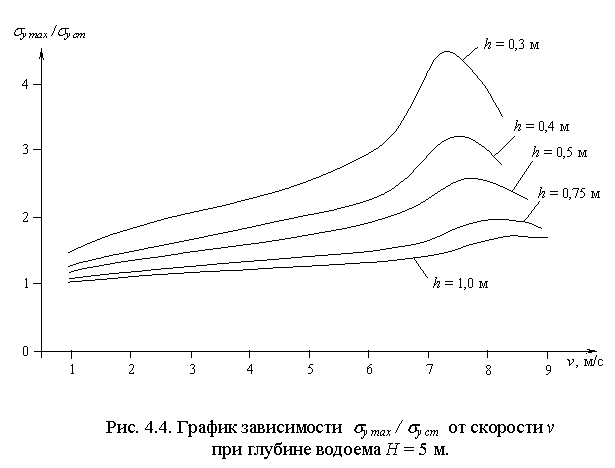
2. Максимумы кривых относительных напряжений, показанных на графиках зависимости  s_{x max} / s_{x ст} ,  s_{y max} / s_{y ст}  от v (рис. 4.3, 4.4), при малых глубинах водоема несколько смещены относительно максимумов прогибов в сторону бóльших значений v, однако смещение это незначительно и составляет величину порядка 2 % от v_р.

Результаты расчета напряженно-деформированного состояния ледяного покрова, полученные изложенным выше численным методом для ряда задач, имеющих известные аналитические решения, сравнивались с этими решениями [2]. Теоретические значения прогибов, рассчитанные численно, сравнивались также с экспериментальными данными, полученными как в лабораторных, так и в натурных условиях [2]. И в том, и в другом случае сравнение позволяет сделать вывод о достаточной точности численных решений.

 .