Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

СОЦИАЛИЗАЦИЯ СТУДЕНТОВ В ПРОФЕССИОНАЛЬНОМ ОБРАЗОВАНИИ

Савва Л. И., Солдатченко А. Л., Плотникова Е. Б., Рабина Е. И., Рязанова Л. С.,

5.2. Моделирование процесса повышения качества математического образования студентов университетов с применением модульно-рейтинговой оценки как средства

Прежде, чем перейти к моделированию процесса повышения качества математического образования студентов университетов, охарактеризуем МРО как педагогическое средство.

Учёные выделяют следующие компоненты МРО: модульную организацию образовательного процесса и рейтинговую оценку знаний [34, 37 и др.]. Рассмотрим сущность данных компонент.

Рейтинговая оценка является одной из современных форм систематического контроля качества образования и используется во многих вузах в сочетание с модульной организацией учебного процесса. Принцип контроля результатов обучения тесно связан с выбором шкалы оценки знаний. Определим место, занимаемое рейтинговой оценкой в классификации оценочных шкал. В разные периоды истории России для оценки знаний обучаемых использовались различные оценочные шкалы, в том числе и рассматриваемая в данном исследовании рейтинговая шкала оценок.

Наиболее известна классификация оценочных шкал, предложенная В.В. Гузеевым [9], рис. 5.1.

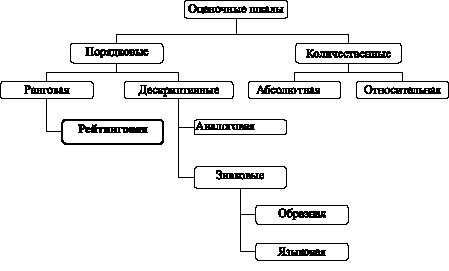
Рис. 5.1. Классификация оценочных шкал (по В.В. Гузееву)

Как видно из схемы, рейтинговая оценка является частным случаем ранговой шкалы оценок, имеющей целью построение иерархического списка обучаемых. Рейтинг – это число, которое выводится в результате опроса субъективного мнения экспертов либо путем набора очков (пунктов, баллов). В конце учебного периода все очки, набранные учеником, суммируются, выводится его рейтинг. После этого множество учеников можно ранжировать по возрастанию рейтингов. Среди очевидных достоинств рейтинговой системы оценки В.В. Гузеев отмечает стимуляцию учебной активности, среди недостатков – субъективизм экспертного способа оценки [9].

В рассмотренной литературе приведены различные классификации рейтинговой оценки. Большинство авторов [18, с. 34] выделяют предварительную, текущую и итоговую рейтинговую оценки. В основе такой классификации лежит этап применения рейтингового контроля: является рейтинговая оценка кумулятивной (накопленной за определённый промежуток времени) или разовой (полученной на аттестационном мероприятии).

Другой подход основан на масштабе (уровне) применения рейтингового контроля: дисциплина, кафедра, факультет, вуз [13, с. 67]. В этом случае выделяют предметный, кафедральный и общий рейтинги.

Цель рейтинговой оценки мы видим в объективной оценке качества математического образования путём установления соотношения между запланированным и полученным качеством образования, а также в стимуляции учебно-познавательной активности студентов. Конкретизируем цель, выделив задачи рейтинговой системы.

К задачам рейтинговой оценки качества образования мы относим:

– повышение уровня организации образовательного процесса, стимулирование ритмичной семестровой работы студентов;

– повышение уровня мотивации студентов к освоению образовательных программ;

– своевременную коррекцию образовательного процесса.

Уточним понятие «рейтинг». Анализ показал, что различные авторы выделяют следующие качественные характеристики понятия «рейтинг»:

– рейтинг это количественная оценка знаний;

– рейтинг может иметь как накопительный (кумулятивный), так и разовый характер;

– рейтинг подразумевает планирование качества обучения;

– показывает соотношение запланированных и полученных знаний;

– рейтинговый контроль использует порядково-ранговую оценочную шкалу [13, 144].

Основной характеристикой рейтинга, по нашему мнению, является количественное представление результатов обучения, поэтому в нашем исследовании мы придерживаемся определения, данного А. Чучалиным, О. Боевым: рейтинг это количественный показатель качества образования студентов. Рейтинговая система оценки качества освоения образовательной программы предполагает текущий контроль успешности познавательной деятельности студента в течение семестра и итоговый контроль в период сессии. Основной принцип данной системы заключается в определении соответствия фактических результатов образования (знаний, компетенций) запланированным [34]. Вычисляется рейтинг как процентное соотношение запланированных и полученных баллов по формуле (5.1):

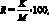(5.1)

где R – итоговый рейтинг студента; K – кумулятивный рейтинг студента (набранные баллы); M – запланированное качество образования, выраженное в баллах.

Учёные выделяют следующие этапы применения рейтинговой оценки:

1. Количественное (балльное) выражение запланированного качества образования, то есть установка максимально возможного балла M.

2. Набор студентами кумулятивного рейтинга K посредству текущего контроля результатов их образовательной деятельности и коррекция учебного процесса.

3. Вычисление по формуле (1) итогового рейтинга R и перевод рейтинговой оценки в традиционную, пятибалльную.

Все этапы рейтинговой оценки обладают достаточной гибкостью, взаимосвязаны и на практике представляют собой логически завершённый, цельный процесс.

Как отмечено выше, основной принцип рейтинговой оценки заключается в определении соответствия фактических результатов образования (знаний, компетенций) запланированным.

Особенности рейтинговой оценки, по нашему мнению проявляются в следующем:

1) данная оценка активизирует ритмичную, самостоятельную работу студентов;

2) вносит дух соревнования в студенческую среду;

3) обеспечивает дифференцированный подход к студентам;

4) снижает риск субъективного подхода преподавателя к студенту при оценке знаний.

При расчете рейтинга удобно опираться на структурные элементы учебного материала, а их, в свою очередь, оптимально можно построить, используя модульную организацию учебного процесса.

Рассмотрим сущность модульного обучения. Центральным понятием которого является «модуль». Ряд зарубежных авторов (В. Гольдшмидт, М. Гольдшидт и др.) понимают под модулем формирование самостоятельной единицы учебной деятельности, помогающей достичь строго определённых целей. Несколько иначе определяет суть модуля Дж. Рассел, а именно, как построение автономных порций учебного материала [40]. Автор технологии контекстного обучения А.А. Вербицкий рассматривает совокупность деятельностных модулей как модель работы специалиста [6, с. 24].

В литературе встречаются различные определения понятия «учебный модуль». Шхацевой К.Л. выделены следующие определения учебного модуля [37, с. 51]:

1. Модуль это единица государственного учебного плана по специальности, представляющая набор учебных дисциплин, отвечающий требованиям квалификационной характеристики.

2. Модулем называется организационно-методическая междисциплинарная структура, представляющая собой набор тем (разделов) из разных учебных дисциплин, необходимых для освоения одной специальности, обеспечивающая междисциплинарные связи учебного процесса.

3. Под модулем понимают способ интегрированности определённого кванта знаний.

4. Модуль это средство междисциплинарных связей.

5. Модуль это форма ориентации на профессионально-видовую созидательную деятельность – конечный результат обучения.

6. Модуль это организационно-методическая структурная единица в рамках одной учебной дисциплины.

Проанализировав данные определения, заключаем, что учебный модуль рассматривают как средство междисциплинарных связей, форму ориентации на конечный результат – созидательную профессиональную деятельность, а также как способ интеграции определённой порции знаний. В нашем исследовании мы проектируем модульную программу для отдельной учебной дисциплины, поэтому выделяем следующие требования к определению учебного модуля:

1) модуль мы рассматриваем как организационно-методическую структурную единицу отдельной учебной дисциплины;

2) определение модуля должно отражать его структуру.

Основываясь на определении Х.М. Инусовой [12] учебный модуль мы понимаем как организационно-методическую структурную единицу учебной дисциплины, которая, отвечая поставленным целям, включает в себя логически завершённую единицу учебного материала, учебно-методический комплекс и систему контроля-коррекции.

Таким образом, модульная организация образовательного процесса предполагает разбиение учебной программы на отдельные модули, каждый из которых, отвечая поставленным целям, включает в себя логически завершённую единицу учебного материала, учебно-методический комплекс и систему контроля-коррекции. Образовательную программу модульной организации, в литературе (Д.Е. Назаров, К.Л. Шхацева и др.) называют модульной программой. Обучение по модульной программе принято называть модульным обучением [37, и др.]. Цель модульного обучения определяется как создание наиболее благоприятных условий развития личности посредством обеспечения гибкости содержания учебного процесса, приспособление дидактических целей к индивидуальным потребностям личности и уровню её базовой подготовки [2, с. 59].

Сущность модульного обучения, по мнению П.А. Юцявичине, «…состоит в том, что обучающийся может более самостоятельно или полностью самостоятельно работать с предложенной ему индивидуальной учебной программой, содержащей в себе целевую программу действий, банк информации и методическое руководство по достижению поставленных дидактических целей. При этом функции педагога могут варьироваться от информационно контролирующей до консультативно координирующей» [39, с. 10].

Особенности модульного обучения, по нашему мнению, заключаются в следующем: чёткая структуризация учебного материала; возможность коррекции учебного процесса благодаря системе текущего контроля; управляемость и прогнозирование результатов обучения; уменьшение доли «субъективного фактора» в оценке знаний обучаемых. Опираясь на исследования П.А. Юцявичине [38, 238], приводим общий алгоритм проектирования модульной программы:

1. Разработка структуры модульной программы:

а) определение общей дидактической цели модульной программы;

б) выделение интегрирующих целей и определения названий соответствующим модулям;

с) построение структуры модульной программы;

д) Выделение частных целей в составе каждой интегрирующей цели, т.е. определение структуры каждого модуля.

2. Формирование содержания каждого модуля, а именно:

а) постановка дидактических цели, трансформация их в целевую программу действий;

б) структурирование учебного материала;

с) создание методического обеспечения для каждого элемента учебного материала;

д) создание контрольно-измерительных материалов.

Выделяют следующие преимущества модульного обучения: дифференциация, индивидуализация учебного процесса; развитие навыков самостоятельной работы, самообразования студентов; варьирование функции преподавателя от информационно-контролирующей до консультативно-координирующей; возможность нелинейной организации учебного процесса.

Преимущества модульного обучения наиболее полно проявляются, в сочетании с рейтинговой оценкой качества образования, сущность которой рассмотрена выше. Системой контроля, основанной на интеграции рейтинговой оценки и модульного обучения является модульно-рейтинговая оценка (МРО) качества образования. Определим её место среди современных систем контроля.

С сентября 2003 года Россия является участницей болонского процесса, цель которого – формирование единого европейского образовательного пространства. Одним из основных положений Болонского соглашения является переход на европейскую систему зачётных единиц ECTS (European Credit Transfer system). 29 июля 2005 года министром образования и науки РФ А. Фурсенко подписан приказ № 215 «Об инновационной деятельности высших учебных заведений по переходу на систему зачетных единиц».

В 39 российских вузах идёт эксперимент по внедрению в образовательный процесс системы зачётных единиц. Систему зачётных единиц Б.А. Сазонов [24] определяет как «системное определение всех основных аспектов организации учебного процесса на основе использования зачётной единицы (кредита) в качестве меры трудоёмкости учебной работы, выражающей совокупность всех составляющих, связанных с организацией учебного процесса». Б.А. Сазонов отмечает, что «важнейшей составляющей системы зачётных единиц является рейтинговая система оценки знаний».

В практике вузов в настоящее время применяются различные вариации и упрощения ECTS, одной из них является кредитно-рейтинговая система. Учёные центра академической мобильности Томского политехнического университета А. Чучалин и О. Боев [34] определяют кредитно-рейтинговую систему как систему количественной оценки содержания образовательной программы с точки зрения планируемых результатов её освоения – приобретаемых знаний, компетенций и методологической культуры. Применяемая нами МРО использует основные компоненты и принципы кредитно-рейтинговой системы, поэтому рассмотрим сущность последней.

Образовательная программа разбивается на N семестровых модулей (курсов, дисциплин) и оценивается условным числом кредитов. Под кредитом понимается количественная оценка содержания образовательной программы. Затем, каждому модулю (курсу, дисциплине) присваивается определённое число кредитов, согласно «весу» этой дисциплины в учебном процессе. Чем выше значимость дисциплины, чем больше времени, сил тратят студенты на её освоение, тем большим числом кредитов она оценивается. Рейтинг каждого студента является показателем его успеваемости по дисциплине и определяется как произведение запланированных на эту дисциплину кредитов и кумулятивного (накопительного) рейтинга студента. Таким образом, фактический результат освоения студентом всей образовательной программы R будет определяться по формуле 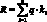(5.2):

(5.2)

где q – кумулятивный рейтинг студента по i-модулю (дисциплине); k – количество запланированных на i-модуль кредитов; n – количество модулей (дисциплин); R – результат освоения образовательной программы.

Наряду с модульной организацией учебного процесса и рейтинговой оценкой знаний, кредитно-рейтинговая система предполагает наличие единого механизма учёта трудоёмкости учебных дисциплин в зачётных единицах. Реализация данного механизма возможна только на уровне вуза. Поэтому, для повышения качества математического образования студентов университета мы использовали МРО, основанную на основных компонентах кредитно-рейтинговой системы и системы зачётных единиц – модульной организации учебного процесса и рейтинговой оценки знаний, но не использующую механизм кредита.

В нашем исследовании МРО мы рассматриваем как педагогическое средство повышения качества математического образования и социализации студентов. Анализируя приведённые в литературе определения педагогического средства, его назначения, виды классификаций мы сделали следующие выводы:

Целью применения педагогических средств является организация, осуществление педагогического процесса, а также развитие учащихся.

Выделяют педагогические средства обучения и педагогические средства воспитания.

Среди средств обучения выделяют материальные и идеальные средства. К материальным относят средства-инструменты: учебники, пособия, помещения, оборудование и т.д. П.И. Пидкасистый идеальное средство определяет как орудие освоения культурного наследия, новых культурных ценностей [21, с. 285]. В качестве идеальных средств обучения выступают речь, письмо, произведения искусства, средства наглядности, учебные компьютерные программы, организующая деятельность учителя, методы и формы организации учебной деятельности, вся система обучения данного учебного учреждения.

Среди средств обучения выделяют также объекты и процессы, которые служат источником учебной информации и инструментами (собственно средствами) для усвоения содержания учебного материала, развития и воспитания учащихся.

Анализ компонент МРО, а также приведённые характеристики педагогического средства позволяют нам констатировать следующее:

В рамках нашего исследования МРО мы рассматриваем как средство обучения.

Применение МРО положительно сказывается на качестве математического образования, так как:

1) модульно-рейтинговая организация учебного процесса стимулирует студентов на активную, ритмичную работу, развивает навыки самообразования, самоуправления;

2) МРО активизирует деятельность преподавателей;

3) МРО объективно, систематично и комплексно оценивает изменения качества математического образования. Повышение качества математического образования студентов увеличивает их шансы на успешную социализацию в современном обществе.

МРО мы рассматриваем как идеальное средство обучения, средство контроля, поскольку данная оценка структурирует образовательный процесс на модули и использует рейтинговый контроль.

Мы рассматриваем МРО как средство развития математических компетенций студентов, приобретения ими опыта творческой деятельности и социализации в обществе с современным уровнем развития производственных технологий.

На основании вышеизложенного мы рассматриваем МРО как педагогическое средство организации учебного процесса посредству его модульного структурирования и использования рейтинговой оценки, как средство развития математических компетенций и опыта творческой деятельности студентов.

Перейдём к моделированию процесса повышения качества математического образования студентов университета с применением МРО как основного средства и обоснуем комплекс организационно-педагогических условий обеспечения эффективности данной модели.

Модель в педагогике – созданная или выбранная исследователем система, воспроизводящая для цели познания характеристики (компоненты, элементы, свойства, отношения, параметры и т.п.) изучаемого объекта и вследствие этого находящаяся с ним в таком отношении замещения и сходства, что ее исследование служит опосредованным способом получения знания об этом объекте и дает информацию, однозначно преобразуемую в информацию о познаваемом объекте и допускающую экспериментальную проверку [36].

В рамках нашего исследования мы выделяем три этапа моделирования: подготовительный этап, этап разработки модели, этап проверки её качества. Первый этап направлен на определение цели, объекта, методов и средств моделирования. Второй этап связан с разработкой и преставлением модели, её описанием и характеристикой. Третий этап связан с экспериментальной проверкой её педагогических условий, методики в практике вуза и оценкой их эффективности.

Целью моделирования для нас является повышение качества математического образования студентов университета с применением МРО. На основании изучения данной системы нам необходимо выделить комплекс организационно-педагогических условий обеспечения эффективности рассматриваемого процесса.

Предметом моделирования является процесс повышения качества математического образования студентов университета. В этой связи мы уточним особенности, этапы, определение МРО применительно к рассматриваемому процессу.

В вузах страны ведётся экспериментальная работа по организации учебного процесса с применением различных вариантов МРО. В литературе выделяют следующие особенности МРО: модульное построение содержания учебного курса и организации его изучения; акцент на самостоятельную работу студентов; наличие чётких критериев оценки различных видов учебной деятельности и их результатов; постоянный контроль и самоконтроль результатов учебной деятельности.

Мы считаем, что важной особенность МРО являются также активизация деятельности преподавателей. Поэтому, в качестве особенностей МРО мы выделяем:

1) объективный, систематичный и комплексный контроль учебных достижений студентов;

2) направленность на коррекцию образовательного процесса;

3) направленность на ритмичную учебную работу студентов в течение семестра, развитие их навыков самообразования, самоорганизации, самоуправления студентов;

4) активизацию субъектов образовательного процесса.

Нами были проанализированы определения понятия «модульно-рейтинговая оценка», данные в различных научных источниках. На наш взгляд, наиболее полным является определение МРО, данное преподавателями кафедры инженерной математики НГТУ [14]: модульно-рейтинговая система представляет собой «нетрадиционную организацию учебного процесса, обеспечивающую развитие навыков успешного самообучения, индивидуальной систематической работы студентов, контроль, стимулирование производительной работы студента и преподавателя, поощрение её успешных результатов». Данное определение учитывает особенности МРО, но не отражает принцип вычисления итогового рейтинга и не указывает, что именно подлежит оцениванию МРО.

Таким образом, уточняя рассматриваемое понятие, мы учитывали следующие положения:

1) качество математического образования мы понимаем как развитость математических компетенций студентов и сформированность опыта творческой деятельности;

2) применение МРО предполагает модульную организацию учебного процесса;

3) основной принцип МРО, заключается в определении результата образования через соотношение полученного и запланированного качества;

4) МРО объективно, систематично и комплексно оценивает изменения качества образования; позволяет своевременно осуществлять коррекцию образовательного процесса; стимулирует студентов на ритмичную работу и самоорганизацию, развивает навыки их самообразования и самоуправления; активизирует деятельность субъектов образовательного процесса.

Под модульно-рейтинговой оценкой качества математического образования студентов университета мы понимаем такую объективную, систематичную и комплексную оценку математических компетенций и опыта творческой деятельности студентов, полученных при освоении модульно-рейтинговой программы путём соотношения фактического качества образования и запланированного, которая позволяет своевременно осуществлять коррекцию образовательного процесса, стимулировать ритмичную работу и самоорганизацию обучающихся, развивать их навыки самообразования и самоуправления при педагогической поддержке преподавателя.

Цель МРО – повышение качества математического образования студентов университета. По нашему мнению, данная цель может быть достигнута через решение следующих задач:

1) формирование у студентов университета математических знаний;

2) формирование у студентов университета репродуктивных математических умений в ходе решения типовых задач;

3) развитие действенности продуктивных и творческих математических умений в ходе решения нетиповых задач и задач-проблем;

4) формирование ценностей и личностных качеств.

Рассматривая компоненты МРО, мы выделили этапы проектирования модульной программы: разработка структуры модульной программы и формирование содержания каждого модуля; и этапы применения рейтинговой оценки: количественное выражение запланированного качества образования, набор студентами кумулятивного рейтинга по результатам текущего контроля и коррекция учебного процесса, вычисление итогового рейтинга.

Проанализировав этапы каждого из компонент МРО, мы определили, что этапами МРО выступают, рис. 5.2:

1) проектирование модульной программы;

2) внедрение рейтинговой оценки и коррекция образовательного процесса;

3) вычисление рейтинга и итоговая аттестация.

Этап проектирования МРО (на рисунке отмечен цифрой «1») заключается в разбиение семестрового курса учебной дисциплины на n обучающих модулей, планируемое качество каждого модуля количественно выражается в баллах, M. Затем, учебный материал структурируется на три элемента: теоретический, практический и творческий.

В течение второго этапа рейтинговой оценки и коррекции образовательного процесса (на рисунке цифра «2») студенты накапливают кумулятивный рейтинг, K.

Это происходит путём оценивания в баллах всех видов их учебной деятельности: посещений лекций, работы на семинарах, выполнения учебных заданий. Отметим, что величина кумулятивного рейтинга не может превышать установленный на первом этапе максимальный балл модуля. По завершении изучения студентами всех модулей вычисляется кумулятивный рейтинг семестрового курса как сумма рейтингов каждого модуля.

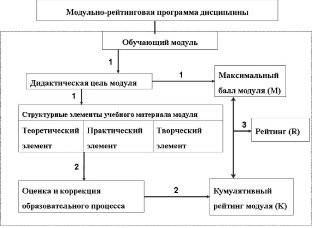
Рис. 5.2. Этапы МРО.
Примечание: этапы МРО на рисунке обозначены цифрами

На третьем этапе вычисления рейтинга и итоговой аттестации (на рисунке цифра «3») происходит подсчёт рейтинга каждого студента как процентного отношения полученного качества образования к запланированному, выраженных в баллах.

В нашем исследовании мы рассматриваем МРО как педагогическое средство, основанием для этого служит то, что эта оценка организует образовательный процесс, структурируя его на модули, и использует рейтинговую оценку, как инструмент усвоения студентами математических компетенций, приобретения ими опыта творческой деятельности.

Перейдём к описанию второго этапа моделирования: разработке структуры и содержания модели повышения качества математического образования студентов университета с применением МРО.

Модель повышения качества математического образования студентов университета с использованием МРО представлена четырьмя взаимосвязанными компонентами: нормативно-целевым, в состав которого входят социальный заказ, цель, задачи, а также принципы; организационно-содержательным, вбирающим модульно-рейтинговую программу курса «Практикум на ЭВМ», комплекс педагогических условий, этапы МРО; методическим, содержащим методы, средства и формы; оценочно-результативным, включающим критерии, уровни и результат, рис. 6.3.

Модель отражает требования, предъявляемые обществом к качеству математической подготовки студентов университета, основные идеи исследования, организацию процесса (цель, содержание, основные этапы модульно-рейтинговой оценки, педагогические условия, результат) и критерии оценки его эффективности. Рассмотрим компоненты представленной модели более детально.

Первым компонентом модели выступает нормативно-целевой компонент, так как мы считаем необходимым определить цель рассматриваемого процесса, прежде чем приступить к его реализации. В завершении процесса достигнутый результат мы сравним с поставленной целью, тем самым определим его эффективность. В состав нормативно-целевого компонента вошли: социальный заказ, цель, задачи и принципы. Выявление социального заказа (повышение качества математического образования в процессе профессиональной подготовки в вузе) определило цель разрабатываемой модели как повышение качества математического образования студентов университета с применением МРО. Достижение цели, по нашему мнению, будет способствовать социализации молодых специалистов. Задачи, через решение которых возможно достижение цели отражены в модели. Их решение основывалось на реализации принципов модульного, компетентностного, личностно-ориентированного и задачного подходов, которые составляют основу нормативно-целевого компонента модели.

Введение следующего, организационно-содержательного компонента модели связано с необходимостью определить содержание рассматриваемого процесса и его этапы. Элемент «содержание» содержит модульно-рейтинговую программу курса «Практикум на ЭВМ» для специальности Прикладная математика и информатика. Внедрение МРО осуществлялась нами в три этапа и дополнено комплексом организационно-педагогических условий, представленным ниже.

Следующим компонентом модели является методический компонент, включающий основное педагогическое средство (МРО) и дополнительные (правила, памятки, задачи, задания, тесты, анкеты, диалог, вопросы, беседы, электронные и технические средства); формы организации обучения (практикумы, консультации, самостоятельную работу, групповую дискуссию, контрольные работы, зачёт); методы (тестирование, анкетирование, объяснение, анализ, синтез, упражнение, наблюдение, рефлексивные методы).

Последний компонент модели, оценочно-результативный, включает в себя обоснованные нами критерии, показатели, диагностические методики и результат. Нами выявлены низкий, средний, высокий уровни качества математического образования студентов университета и дана их характеристика. Данные уровни определяются следующими критериями и показателями: математические знания (полнота содержания системы знаний, объём системы знаний, прочность знаний); математические умения (полнота сформированности умений, прочность умений, осознанность умений); опытом творческой деятельности (решение студентом типовых, нетиповых и творческих задач); ценностями и личностными качествами (отношение студентов к математике, отношение студентов к оценке своего учебного труда, сформированность ответственности за результаты учебного труда, сформированность самостоятельности у студентов университета). Результат модели сформулирован нами как переход студентов университетов на более высокий уровень качества математического образования.

Важно, что разработанная нами авторская модель имеет определенную закономерность. Все ее компоненты расположены в порядке последовательности: от нормативно-целевого до критериально-оценочного. Однако связь прослеживается не только между четырьмя компонентами модели, но и внутри каждого из них, обеспечивая продвижение от одного элемента к другому по указанному направлению. Определенная нами связь всех структурных составляющих компонентов и элементов в модели создаёт её целостность.

Для обеспечения эффективности описанной модели нами был разработан комплекс организационно-педагогических условий. Мы не будем останавливаться на широко освещённом в педагогической литературе определении «организационно-педагогические условия», уточним его применительно к рассматриваемому процессу.

Организационно-педагогические условия обеспечения эффективности процесса повышения качества математического образования студентов университета с применением МРО мы понимаем как: совокупность внешних объектов, обстоятельств образовательной среды и внутренних особенностей (состояний, качеств) МРО, которая обеспечивает повышение качества математического образования студентов университета.

Обоснуем выделенный нами комплекс условий. Рассмотрим первое условие «Осознание студентами объёма, содержания и выбора последовательности изучения материала в структурированном модуле». Данное условие введено нами для того, чтобы с самого начала семестра студенты осознали объём, содержание, структуру каждого учебного модуля, что поможет им спланировать индивидуальную учебную траекторию. Студенты должны осознать необходимость планомерной, ритмичной учебной работы, правильно распределить свои силы для занятий в течение всего семестра. Такой настрой на учёбу поможет им набрать высокий рейтинг и обеспечит высокую успеваемость, а в дальнейшем, во «взрослой» жизни, организованность и умение планировать свои действия станут опорой в движении по профессиональной лестнице, в успешной социализации.

«Осознание» в психологии понимается как акт сознания, в основе которого лежит обобщение собственных психических процессов. «Сознание» это рефлексия субъектом действительности, своей деятельности, самого себя [30]. Анализ психолого-педагогической литературы показал, что термин «осознание» близок по смыслу к «пониманию», которое трактуется как «состояние сознания, вызванное внешними или внутренними воздействиями и фиксируемое субъектом как уверенность в адекватности воссозданных представлений содержанию воздействия. Без понимания, как особого состояния субъекта, не возможно продолжение общения, координация действий и какие-либо другие осмысленные действия» [19, с. 447]. Для понимания характерно ощущение ясной логической упорядоченности, организованности рассматриваемых явлений.

Таким образом, каждый студент должен ясно понять: сколько заданий ему нужно выполнить, какие именно, когда и в какой последовательности. Соотнеся «цену» задач с их сложностью и временем, которое будет затрачено на решение, студент разрабатывает для себя индивидуальную учебную траекторию: выбирает, какие именно учебные задачи, в какой последовательности и в какой срок ему выполнять. Именно разработку студентом такой индивидуальной учебной траектории мы понимали как факт осознания им объёма, содержания и выбора последовательности изучения учебного материала.

Учебный материал модуля структурирован нами на три элемента: теоретический, практический и творческий. Теоретический элемент содержит лекции в электронном и печатном виде, ссылки на различную литературу, рекомендованную для обязательного и дополнительного изучения. Практический элемент включает учебные задания, лабораторные и практические работы, комплекс задач (наполнение данного элемента может меняться в зависимости от дисциплины). По сути, содержание практического элемента – это типовые задачи, то есть задачи, решаемые путём «буквального непреобразованного использования усвоенных алгоритмов деятельности» и нетиповые задачи, то есть требующие «предварительного преобразования усвоенных методик и их приспособления к ситуации» [4, с. 63]. Творческий элемент содержит задачи-проблемы. Под «задачами проблемами» мы, вслед за В.П. Беспалько, понимаем «задачи, алгоритм решения которых неизвестен и не может быть прямо получен путём преобразования известных методик».

Методологической основой данного условия выступают принципы модульного подхода в образовании: модульности, структуризации учебного материала. Для того, чтобы с первого занятия в семестре студентами был осознан объём, структура, содержание учебного материала каждого модуля и выбрана последовательность его изучения, мы подробно объясняли студентам:

1) количество модулей, определённых к изучению в этом семестре, цель каждого модуля;

2) структуру каждого модуля и его содержание;

3) уровень сложности каждой задачи, её балльная оценка, дата сдачи;

4) правила начисления рейтинга и его перевода в итоговую оценку.

В компьютерной сети факультета размещались соответствующие памятки, правила, их изменения в течение семестра не допускались.

Обоснуем введение второго условия: развитие творческой активности студентов в ходе решения комплекса задач разного уровня сложности. Данное условие направлено на развитие творческой активности студентов, которое являются необходимыми условиями получения математического образования высокого уровня. Качество математического образования студентов университета мы понимаем как развитость их математических компетенций и сформированность опыта творческой деятельности. Математические компетенции это не только математические знания, умения, значимые качества и ценности личности, но и, в большой степени, развитое аналитическое мышление. Развитие аналитического мышления происходит преимущественно в процессе решения задач.

Анализ литературы показал, что «активность» трактуется как деятельностное отношение человека к миру, способность человека производить общественно значимые преобразования материальной и духовной среды на основе освоения общественно-исторического опыта человечества, проявляющаяся в творческой деятельности, волевых актах и общении [22, с. 27]. Выделяют репродуктивную (воспроизводящую) и творческую активность личности. Творческая активность определяется как высший уровень активности в учебно-познавательной деятельности.

Творческая активность в процессе получения математического образования тесно связана с интеллектуальной активностью. Данное понятие в психологии определяется через «мышление», которое понимают как отражение действительности в таких объективных её свойствах, связях и отношениях, которые недоступны непосредственному чувственному восприятию. Различают аналитическое и интуитивное мышления. Аналитическое мышление характерно тем, что его отдельные этапы отчетливо выражены и думающий может рассказать о них другому человеку. Важнейшей составляющей аналитического мышления является синтез индуктивного и дедуктивного этапов движения мысли: восхождение от опыта к теории и движение от теории к практике. Одной из целей математического образования является развитие способности учащихся проходить этот цикл мыслительной деятельности в том и другом направлении .

«Интеллектуальная активность» это не стимулированное извне продолжение мышления [19, с. 206]. Существуют три качественных уровня интеллектуальной активности:

1) пассивный, когда человек остаётся в рамках заданного или первоначально найденного способа действия; соответствует продуктивному решению задач;

2) эвристический, когда человек проявляет интеллектуальную активность, не стимулированную ни внешними факторами, ни субъективной оценкой неудовлетворенности результатов деятельности; нахождение новых, оригинальных способов решения;

3) креативный, для него характерно, что обнаруженная субъектом эмпирическая закономерность становится для него самостоятельной проблемой, ради изучения которой он готов прекратить предложенную извне деятельность, начав другую мотивированную уже изнутри; этот уровень соответствует теоретическим открытиям.

Методологической основой реализации данного условия выступают принципы личностно-ориентированного и задачного подходов. Принципами личностно-ориентированного подхода являются, в том числе, индивидуализация, дифференциация обучения и принцип рефлексивной активности. Реализуются данные принципы путём использования в учебном процессе комплекса задач разного уровня сложности.

Процесс повышения качества математического образования студентов университета носит поэтапный характер и предусматривает их продвижение с одного уровня на другой. Использование задач различного уровня сложности позволяет сделать этот процесс управляемым и личностно-ориентированным.

Обоснуем введение третьего условия: формирование ответственности студентов за результаты и своевременное выполнение учебных заданий. Ответственность является личностным качеством, выражающим склонность личности исполнять свои обязанности и давать отчёт за свои действия перед обществом и самим собой. Выделяют различные «зоны ответственности»: гражданскую, моральную, профессиональную и т.п. По мнению психологов, ответственное отношение к порученным обязанностям и их исполнению формируются у детей ещё в дошкольном возрасте. Несмотря на это многие студенты, особенно младших курсов, показывают невысокий уровень учебной ответственности: у них наблюдается неполное осознание учебных обязанностей и недостаточная требовательность к себе лично. Если рассматривать ответственность как ценность личности, определяющую контроль её поведения, учения, образования, то правомерно утверждать, что качество обучения зависит от уровня ответственности студентов за процесс учения и его результат.

Анализ психолого-педагогической литературы позволил выявить, что, определяя термин «ответственность», в качестве родового понятия различные авторы используют: «качество», «способность» личности, «долг», «компетенция». Сформулированный в Болонском соглашении компетентностный подход рассматривает качество образования выпускника вуза как набор профессиональных компетенций. В предыдущем параграфе нами проведён анализ понятия «компетенция» и, в частности, сделан вывод о том, что сформированная компетенция предполагает готовность личности использовать приобретённые знания, умения, навыки в профессиональном контексте. Такую готовность обеспечивают и поддерживают определённые качества и ценности личности. Ответственность за результаты учебного труда Чумичёва Р.М. [33] рассматривает как личностную (социально-организационную) компетентность студентов, как личностное качество, позволяющее студентам эффективно осуществлять образовательную деятельность в вузе, реализоваться в профессии в дальнейшем.

Компетентностный подход реализован в нашем исследовании следующими принципами:

1) сознательности;

2) взаимной ответственностью субъектов обучения за его качество;

3) рефлексивной активности.

Ответственность является тем внутренним механизмом, с помощью которого человек стремится к результату. Результатом обучения для нас является кумулятивный рейтинг студента – количественный показатель его успеваемости. Чувство ответственности за результаты своего учебного труда стимулирует студентов запланировать для себя высокий рейтинг, чтобы набрать его, не пропускать занятия, браться за выполнение более сложных учебных заданий, проявлять настойчивость в их выполнении, стремиться своевременно отчитаться перед преподавателем о выполненной работе. В случае неудачи (набранный к концу семестра рейтинг ниже, чем запланировано самим студентом) студент с развитым чувством ответственности объективно видит недочёты в своей учебной работе, а не перекладывает вину на преподавателя или внешние обстоятельства. Такой подход к учёбе, как показывает практика, повышает успеваемость студентов.

Данные условия представляют собой комплекс, так как ориентированы на поэтапное применение МРО. Помимо МРО на каждом её этапе мы пользуемся дополнительными педагогическими средствами, с помощью которых осуществляется комплексное применение выделенных условий. Условия взаимодополняют друг друга, реализуя принципы различных подходов на каждом этапе МРО.