Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

СОЦИАЛИЗАЦИЯ СТУДЕНТОВ В ПРОФЕССИОНАЛЬНОМ ОБРАЗОВАНИИ

Савва Л. И., Солдатченко А. Л., Плотникова Е. Б., Рабина Е. И., Рязанова Л. С.,

5.3. Практико-ориентированная методика повышения качества математического образования студентов университета с применением модульно-рейтинговой оценки

Рассмотрим методику реализации условий на каждом этапе МРО на примере дисциплины «Практикум на ЭВМ» для специальности 010501 «Прикладная математика и информатика». Во 2 семестре на изучение данной дисциплины отводится 85 часов, из которых самостоятельная работа – 17 часов, практические занятия – 68 часов, лекционных часов для этой дисциплины не предусмотрено. Цель данного учебного курса – научить студентов решать с помощью ЭВМ практические задачи, применять на практике знания, полученные при изучении математических дисциплин. Форма итоговой отчётности – зачёт. Кумулятивный рейтинг студенты набирают путём сдачи контрольных мероприятий: практических работ и теоретических тестов.

Применение МРО осуществлялась нами в три этапа:

1) проектирование модульно-рейтинговой программы;

2) внедрение рейтинговой оценки и коррекция образовательного процесса;

3) вычисление рейтинга и итоговая аттестация; в рамках комплекса организационно-педагогических условий повышения качества математического образования студентов университета.

Выше обосновано, что данный комплекс организационно-педагогических условий включает в себя:

а) осознание студентами объёма, содержания и выбора последовательности изучения материала в структурированном модуле;

б) развитие творческой активности студентов в ходе решения комплекса задач разного уровня сложности;

в) формирование ответственности студентов за результаты и своевременное выполнение учебных заданий.

Наряду с МРО, которая являлась для нас основным педагогическим средством повышения качества математического образования, мы использовали дополнительные средства: правила, памятки, задачи, задания, тесты, анкеты, опросы, беседы, электронные и технические средства.

На каждом из выделенных этапов применения МРО одно из условий являлось для нас доминирующим, то есть основное внимание уделялось реализации его методов, форм, средств и методических приёмов. Вместе с тем, на каждом этапе МРО условия дополняли друг друга, что отражено в табл. 5.1.

Таблица 5.1

Особенности реализация комплекса организационно педагогических условий по этапам МРО

Примечание: знаком «!» отмечено доминирующее условие на данном этапе МРО.

На первом этапе применения МРО (проектирование модульно-рейтинговой программы) мы посчитали логичным уделить особое внимание реализации принципов модульности, структуризации учебного материала и считать доминирующим первое условие: осознание студентами объёма, содержания и выбора последовательности изучения материала в структурированном модуле.

При проектировании модульно-рейтинговой программы мы опирались на зависимость трудоёмкости различных форм учебной деятельности студентов от количества академических часов, выделенных на ту или иную форму. Баллы вычислялась нами путём применения к количеству часов коэффициентов трудности (K). каждого модуля. Модульно-рейтинговая программа дисциплины «Практикум на ЭВМ» представлена в табл. 5.2.

Установлено, что наиболее рационально подбирать материал для максимально высокого уровня подготовки студентов, разделяя его по уровням сложности. В этом случае у преподавателя есть возможность варьировать содержание обязательной и дополнительной части теоретического элемента.

Практический элемент модуля – задания, лабораторные и практические работы, комплекс задач (наполнение данного элемента может меняться в зависимости от дисциплины). Содержание практического элемента это типовые задачи, т.е. задачи, решаемые путём «буквального непреобразованного использования усвоенных алгоритмов деятельности» и нетиповые задачи – требуют предварительного преобразования усвоенных методик и их приспособления к ситуации. Классификация используемых задач и их примеры приведены нами ниже, при описании второго этапа МРО.

Творческий элемент – данный элемент содержит творческие задания –
задачи проблемы. Под «задачами проблемами» мы, вслед за В.П. Беспалько, понимаем «задачи, алгоритм решения которых неизвестен и не может быть прямо получен путём преобразования известных методик». Пример задачи-проблемы приведён при описании второго этапа МРО.

Учебный материал модуля структурировался нами на три элемента: теоретический, практический и творческий. Теоретический эле-
мент – это задания по итогам изучения теоретического материала, который должен быть усвоен студентами из основных и дополнительных источников: лекций, учебников, в печатном и электронном виде. Содержание этого элемента частично прочитывается на лекциях, некоторый материал предназначен для самостоятельного и дополнительного изучения.

Таблица 5.2

Модульно-рейтинговая программа дисциплины «Практикум на ЭВМ»

Примечание: Бм – максимальный балл, К – максимальный коэффициент трудности.

Три составляющих учебного материала модуля – теоретический, практический и творческий элементы – взаимосвязаны между собой через свои цели и порядок изучения. Показатели первого критерия качества математического образования (полнота и объёма системы знаний, прочность знаний) формируются при изучении теоретического элемента. Цель практического элемента – отработка прочности, осознанности, действенности умений – это показатели критерия «сформированность умений». Цель творческого элемента модуля – формирование опыта творческой деятельности. Таким образом, каждый предыдущий содержательный элемент готовит студентов к выполнению последующего. С другой стороны, каждый из элементов «работает» в той или иной мере на цели других элементов модуля. Так, при решении задачи-проблемы из творческого элемента, зачастую возникает необходимость изучить дополнительный материал теоретического элемента, и наоборот, изучив интересный теоретический материал, студент применяет его на практике. Элемент формирования и отработки умений – практический – адресует студентов к теоретическому и творческому элементам. Структура учебного материала модуля представлена на рис. 5.4.

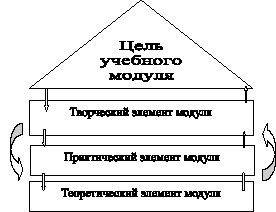
Рис. 5.4. Структура материала учебного модуля

Структурирование учебного материала каждого модуля на взаимосвязанные и дополняющие друг друга теоретический, практический и творческий элементы помогает студентам осознать его объём, содержание и выбрать последовательность изучения материала по дисциплине. Это настраивает студентов на ритмичную учебную работу с начала семестра.

В качестве метода обучения на данном этапе нами выбрано объяснение, соответствующее учебное занятие проводилось в начале семестра в форме консультации и имело целью показать студентам объём и содержание модульно-рейтинговой программы, объяснить им правила начисления баллов и перевода их в итоговую оценку.

Дополнительными средствами на данном этапе были: правила начисления балльной оценки, памятки, беседы, электронные и технические средства. Памятка «Условия набора рейтинга» например, содержит информацию о структуре и содержании модульной программы, о сроках сдачи заданий и их балльной оценке, а также условия промежуточной и итоговой аттестаций, систему «штрафов». Таким образом, данная памятка представляет собой набор таблиц (табл. 5.2 и др.) и пояснения к ним.

Рассмотрим второй этап применения МРО: внедрение рейтинговой оценки и коррекцию образовательного процесса. На данном этапе мы считаем доминирующим второе условие – развитие творческой активности студентов в ходе решения комплекса задач разного уровня сложности. Второй этап применения МРО самый протяжённый по времени, фактически, это весь учебный семестр. Именно на данном этапе студенты изучают новый материал, решают задачи, отчитываются об их выполнении и набирают кумулятивный рейтинг. Мы считаем, что такая деятельность может быть успешной только при высокой творческой активности студентов, поэтому именно второе условие доминирует на данном этапе МРО. На данном этапе мы пользовались принципами задачного и личностно-ориентированного подходов.

Выше нами отмечено, что творческая активность определяется как высший уровень активности в учебно-познавательной деятельности. Так же нами выявлено, что под интеллектуальной активностью понимают не стимулированное извне продолжение мышления. Для качества математического образования значимым является аналитическое мышление, развитие которого происходит преимущественно в ходе решения задач. Развитие творческой активности осуществлялось нами путём решения студентами комплекса задач разных уровней сложности: типовых, нетиповых и творческих. Такая классификация задач основана на выделенных В.П. Беспалько следующих типах учебной деятельности: алгоритмическая деятельность (действие по алгоритму, воспроизводимому по памяти), эвристическая деятельность (самостоятельное преобразование известного алгоритма), творческая деятельность (получение новой информации, исследовательская деятельность) [4, с. 55].

При разработке комплекса задач мы придерживались следующих требований:

1) учёт как специфики изучаемого предмета, так и уровневого характера подготовленности студентов;

2) опора на принципы преемственности и последовательности, обеспечивающих поэтапное включение студентов в деятельность более высокого уровня;

3) комплекс задач должен обеспечивать возможность приобретения новых знаний, умений и навыков, а также развитию творческого потенциала личности.

Творческую активность студентов мы стимулировали следующими приёмами:

1. Бальная оценка находилась в прямой зависимости от сложности задачи и оригинальности её решения. Вычислялась максимально возможная балльная оценка задачи Бм по формуле (формула 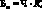(5.3)):

(5.3)

где Бм – максимально возможный балл за решение данной задачи и за реализацию её на ЭВМ; Ч – сумма аудиторных и часов самостоятельной работы, отведённых на её решение; К – коэффициент трудности.

2. Повысить балльную оценку задачи мы могли либо за счёт отведения на её решение большего количества аудиторных и часов самостоятельной работы, либо за счёт повышения коэффициента трудности. При оценивании нетиповой задачи мы использовали ту и другую возможности. Все задачи-проблемы вынесены нами на часы самостоятельной работы, так как алгоритм их решения студенту предстоит построить самостоятельно.

3. За самостоятельный поиск решения, за его оригинальность, рациональность мы начисляли студенту дополнительные баллы, путём повышения коэффициента трудности K.

Опыт показывает, что «цена» творческой задачи должна быть соизмерима с балльной оценкой типовой задачи. В противном случае, студенты часто сразу берутся за решение задач высокого уровня сложности: требующих предварительной проработки теории, решения «тренировочных задач». Не справившись с решением такой задачи, студенты не успевают «добрать баллы» до конца семестра и становятся задолжниками.

Формами обучения были выбраны практикумы, консультации, групповые дискуссии, контрольные работы, самостоятельная работа. В качестве методов взяты: объяснение, анализ, синтез, упражнение, консультации, наблюдение, рефлексивные методы, тестирование. Для поощрения студентов к решению трудных задач мы пользовались рефлексивными вопросами. Так, проверяя у студента решение задачи-проблемы, мы спрашивали его: Какие трудности были встречены при решении и как они были преодолены? По нашему мнению, такие вопросы повышают самооценку студентов, помогают поверить в свои силы взяться за решение новой интересной задачи.

Дополнительными педагогическими средствами на данном этапе применения МРО выступали: задачи, дискуссии, диалог, рефлексивные вопросы, тесты, электронные и технические средства, правила начисления балльной оценки, памятки.

Рассмотрим третий этап применения МРО: вычисление рейтинга и итоговая аттестация. На данном этапе мы считаем доминирующим третье условие, а именно: формирование ответственности студентов за результаты и своевременное выполнение учебных заданий. Третий этап МРО это подведение итогов семестра. Для студента это время рефлексивного анализа результатов своей работы: каков его кумулятивный рейтинг, легко ли будет получить «зачёт», в полную ли силу он занимался, можно ли было достичь лучших результатов, как планировать свою учебную деятельность в следующем семестре? Именно этот этап МРО мы выбрали для формирования ответственности студентов за результаты учебного труда. Реализация данного условия основана на принципах компетентностного подхода:

1) взаимная ответственность субъектов обучения за его качество;

2) создание условий для формирования у обучаемых опыта самостоятельного решения познавательных, коммуникативных, организационных, нравственных и иных проблем, составляющих содержание образования;

3) рефлексивная активность обучаемых.

Формирование ответственности за результаты учебного труда у студентов осуществлялось нами путём поощрения своевременного выполнения ими учебных заданий, для этого мы использовали следующие методические приёмы:

1. Применение системы штрафов. В случае несвоевременной сдачи работы. Каждое учебное задание в начале семестра оценивалось нами в баллах, назначалась дата его сдачи. Если студент «сдавал» работу на одно занятие позже указанного срока, то она оценивалась на 1 балл меньше, на два занятия – на 2 балла меньше, и т.д. Опыт показал, что нецелесообразно уменьшать установленный балл более чем наполовину, независимо от срока задолженности, так как у студентов пропадает стимул выполнять просроченное задание.

2. Приём разъяснения. Правила вычисления балльной оценки своевременно разъяснялись студентам, в компьютерной сети размещались соответствующие памятки.

3. Приём оперативности. Дата выполнения учебного задания, его качество чётко фиксировались преподавателем.

4. Приём анализа работы. В конце семестра нами проводилось анкетирование студентов с целью помочь им проанализировать качество своего учебного труда и сделать выводы о личной ответственности за него.

5. Рефлексивный приём. Нами составлены анкеты, направленные на рефлексивный анализ студентами результатов своего учебного труда.

Формами обучения на третьем этапе были выбраны консультации, групповые дискуссии, где мы вместе со студентами подводили итоги семестра, предметом обсуждения был кумулятивный рейтинг каждого студента, условия добора баллов. Также нами проводилось анкетирование, направленное на формирование ответственности. В качестве методов взяты: объяснение, наблюдение, рефлексивные методы, анкетирование.

Дополнительными педагогическими средствами на данном этапе применения МРО выступали: дискуссии, диалог, рефлексивные вопросы, анкета, электронные и технические средства, правила начисления балльной оценки, памятки.

Подведём итог выполненному нами исследованию. Установлено, что компонентами МРО качества математического образования являются модульная организация образовательного процесса и рейтинговая оценка знаний. В качестве этапов применения МРО нами выделены:

1) проектирование модульной программы;

2) внедрение рейтинговой оценки и коррекция образовательного процесса;

3) вычисление рейтинга и итоговая аттестация.

Особенностями МРО качества математического образования являются:

1) объективный, систематичный и комплексный контроль учебных достижений студентов;

2) направленность на коррекцию образовательного процесса, ритмичную учебную работу студентов, развитие их навыков самообразования, самоорганизации и самоуправления;

3) активизация субъектов образовательного процесса.

Уточнено, что модульно-рейтинговая оценка качества математического образования студентов университета – это такая объективная, систематичная и комплексная оценка математических компетенций и опыта творческой деятельности студентов, полученных при освоении модульно-рейтинговой программы путём соотношения фактического качества образования и запланированного, которая позволяет своевременно осуществлять коррекцию образовательного процесса, стимулировать ритмичную работу и самоорганизацию обучающихся, развивать их навыки самообразования и самоуправления при педагогической поддержке преподавателя.

Обосновано, что структурная модель повышения качества математического образования студентов университета с использованием МРО как средства, состоит из четырёх взаимосвязанных компонент: нормативно-целевого, организационно-содержательного, оценочно-результативного; она основана на принципах модульного, личностно-ориентированного, компетентностного и задачного подходов; позволяет более объективно, оперативно, систематично и комплексно оценивать личностные и образовательные достижения студентов.

Выявлено и доказано, что комплекс организационно-педагогических условий, обеспечивающий эффективное функционирование разработанной модели повышения качества математического образования студентов университета с применением МРО, представлен следующими условиями:

1) осознание студентами объёма, содержания и выбора последовательности изучения материала в структурированном модуле;

2) развитие творческой активности студентов в ходе решения комплекса задач разного уровня сложности;

3) формирование ответственности студентов за результаты и своевременное выполнение учебных заданий.

Апробирована практико-ориентированная методика повышения качества математического образования студентов университета с применением МРО как средства, вбирающая в себя: методы (тестирование, анкетирование, объяснение, анализ, синтез, наблюдение, тренинговые методы, рефлексивные методы); средства (основные – МРО и дополнительные: задачи, дискуссию, диалог, упражнения, тесты, анкеты, правила, технические и электронные средства, рефлексивные задания, вопросы); формы (практикумы, консультации, самостоятельную работу, групповую дискуссию, контрольные работы, зачёты).