Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

СИСТЕМНЫЙ АНАЛИЗ (начальные понятия)

Раков В И,

Лекция 11. Особенности формализованного знания для формирования концептуальности

При исследовании явлений объективной реальности роль начальных моделей играют концептуальные модели, объединяющие, охватывающие и обобщающие конкретности в понимании и толковании и определяющие или обуславливающие метод понимания образов и действительности и метод трактовки получаемых результатов.

Моделирование начинается на этапе формирования представлений об исследуемом явлении и выражается в создании концептуальных моделей, предшествующих множеству предметно-математических, «технических», «технологических» и прочих традиционно понимаемых моделей самого исследуемого явления.

Первая группа причин, порождающих погрешности моделирования и, в частности, ошибки и неточности построения концептуальных моделей, кроется в самой потребности акта сохранения (выражения) психических образов явления объективного мира на искусственных или этнических языках. Вторая группа связана с общественными идеалами и с конкретным для технического направления (объекта, системы, процесса, явления) целеположением (целью).

На процесс формирования концептуальных взглядов о некотором явлении (объекте, процессе, системе) существенно влияют индивидуальные представления и организация концептуального процесса:

– языковое многообразие при восприятии явления;

– языковое многообразие при выражении явления или выражении его некоего языкового образа;

– языковое многообразие при сохранении языкового образа исследуемого явления;

– возможность существования адекватной концептуальности в каждой реальной обстановке и потребность поиска или конструирования подходящей концептуальной модели для текущих обстоятельств;

– относительность (распределённость, аддитивность, сосредоточенность) концептуальности;

– представление концептуальности как развивающегося и бесконечного процесса концептуального прогнозирования;

– экспертность характера выбора концептуальных воззрений.

Компоненты концептуальной среды вносят соответствующий вклад в формирование следующих фундаментальных погрешностей:

– погрешностей оценки различными индивидуумами текущих обстоятельств;

– погрешностей конструирования подходящих концептуальных моделей (исследуемого явления для текущих реальных обстоятельств), являющихся результатом осознанного или неосознанного предвзятого воздействия известных моделей (теорий, исчислений, языков и т.п.) на представления об исследуемом явлении;

– погрешностей степени адекватности (правильности, реальности) восприятия структуры явления, места и роли человека, способа организованности концептуального процесса;

– погрешностей экспертных усилий при обобщениях, выборе или коллективных оценках.

К фундаментальным погрешностям надо отнести и те, которые характерны всему процессу создания концептуальной модели и связаны с выбранными стратегиями языкового и концептуального моделирования [рис. 26; лекция 10].

Утверждаясь в важности концептуальной модели, трудно выделить какие-либо более или менее ценные её качества, будь то выраженное в модели представление о месте образов исследуемых явлений в системе знаний человека, или выраженное в модели заключение о том, как будут соотносимы трансформируемые образы с реальным миром, или фактически обуславливаемый моделью «механизм» различного понимания и трактовки.

Концептуальная модель, несмотря на своё смысловое предназначение быть начальной моделью, несомненно, является таковой только в системном плане. И поэтому само понимание системной конкретности её выражения, её системной выразительной сущности, наконец, понимание процесса конструирования и самой формы записи этой сущности играет особо значимую роль в процессе формирования представлений о концептуальном базисе системного анализа.

Исходим из того, что концептуальность – это:

– связь сознания человека с внешним миром в форме языковой сущности конкретных явлений;

– связь осознанного образа явления с объективной реальностью в границах целеположения (смысла) и явления и образа в его осознанной (осознаваемой) среде;

– понимание в рамках системы знаний и ценностей человека (его мировоззрения), подтвержденное опытом восприятия окружающего мира.

Тогда можно сказать, что концептуальность – это фактически некоторое обобщенное знание, неразрывное с его языковой формой, и ощущения, и выражения или, попросту, языковой формой представления. В связи с этим достаточно важно (актуально) понимание того, насколько известные направления по представлению знаний являются или могут быть подходящими для отражения выразительной сущности концептуальности.

Трудно отказаться от мысли, что представление знаний осуществляется человеком на общем фоне его физиологической, эмоциональной (чувственной) и интеллектуальной деятельности. Несмотря на их определенную взаимосвязь и взаимную обусловленность, считают, что ведущая роль в этой деятельности отводится интеллектуальной составляющей.

До конца еще не выяснен механизм оперирования идеями (смыслом), образами, состояниями пустоты (освобожденного сознания), сомати и т.п. Бесспорно то, что мыслительный процесс – это основа интеллектуальной деятельности, существо которого выражено такими представлениями и терминами, как понимание, познание, осмысливание, размышление. Ему характерны чередующиеся фазы (этапы) языкового и неязыкового выражения[95].

Языковая фаза – это результат материализации мыслей и чувств. При этом происходит формулирование целей, стратегий и результатов поиска, логических последовательностей, равносильных и неравносильных преобразований, выводов и т.д.

Неязыковая фаза – это работа некоего мыслительного аппарата, когда сознанием не фиксируются цели, стратегии поиска, результаты, выводы. Результатом неязыковой фазы является начало языкового этапа, который характеризуется общепризнанными методами позна-
ния – анализом, синтезом, моделированием[96]. В результате работа мысли приводит к языковой формулировке.

Несмотря на формальную неопределенность неязыкового этапа, нельзя отрицать существование фактов, которые характеризуют его с различных сторон: неязыковые индукция и урим[97], рациональные (правдоподобные) рассуждения[98], психометрия и другие материалистически понимаемые или до конца не осознанные человечеством различные проявления мыслительной деятельности[99]. Фазы мыслительного процесса объединены одной функцией: они вырабатывают знания. Если оставаться в рамках научного познания, то можно настаивать на том, что неязыковой этап всегда приводит к новому знанию, осознаваемому человеком в момент языковой материализации мысли или чувства.

Знания, получаемые на языковом этапе, могут представляться двояко: вытекать из имеющейся их совокупности, как результат последовательных выводов, композиций отношений, или являться результатом коррекции, дополнения, изменения ранее осознанного их множества, например в результате получения знания о реальной деятельности. В любом из этих случаев знания обусловлены языком. Их можно отнести к новым знаниям только в плане ожидаемых из определенного множества результатов.

Представление знаний, по сути, связывают с формализованным представлением процессов мышления (понимания, познания, осмысливания). В частности, такие представления в плане формальной (автоматической, машинной) реализации начинаются с идей А. Тьюринга, Дж. фон Неймана, А. Ньюэлла, Г.А. Саймона, М. Минского и др., существенно расширенных достижениями научных школ академиков В.М. Глушкова, А.И. Берга, Н.М. Амосова; профессоров И.К. Бельского, Д.А. Поспелова, Ю.И. Клыкова, В.А. Горбатого.

Техническая идеология устройств искусственного интеллекта в известной степени – это реализация разнообразных баз знаний, различных языковых представлений и мыслимых и немыслимых процессов формального вывода. Человек формирует начальное множество (базу) знаний, участвует в оценке новизны полученных знаний, поиске «оптимальной» стратегии их получения и эффективного использования для реализации меняющихся целей. Представление формализованных знаний связывают с разработкой моделей предметной области, адекватно отображающих понимание человеком реального мира[100] и полагают, что правильно выбранный формальный способ представления знаний обеспечивает и продуктивность исследований, и эффективность проектируемых систем.

Модели представления знаний делят на три класса: декларативные, процедурные и семантические. В декларативных представлениях описание состояний – это множества утверждений, в значительной степени независимых от того, где их использовать. При процедурном представлении знаний информация дается в виде процедур, программ, задающих алгоритм преобразования между единицами знаний для данной предметной области.

Полагают, что семантическое представление предметной области является некоторым аналогом способа представления знаний у человека. Его определяющими характеристиками являются описание объектов мира на уровне естественного языка; накопление знаний в относительно однородной памяти, включая вновь поступившие факты; определение ряда унифицированных семантических отношений между объектами, которым соответствуют унифицированные методы вывода.

Существуют разные способы семантического представления. Базу направлений по формализации знаний и оперирования с ними для решения задач управления так или иначе составляют исчисление предикатов[101] и представления о нечетких (размытых, неточных) множествах[102], а реализация связана с так называемыми языками представления знаний (языками смысла)[103].

Предикаты[104]. Если высказывания рассматриваются не как отдельные компоненты, как в исчислении высказываний, а как некоторая связь между субъектом (существительным) и предикатом (глаголом), то становится понятным, почему исчисление высказываний недостаточно для анализа множества рассуждений.

Пусть M = {m1, m2, ..., mn} – предметная область, где mi – некий предмет (). Пусть P(mi), Q(mj, mk) и т.п. – обозначение высказываний об этих предметах. Пусть x – обозначение любого предмета из данной предметной области.

Логическая функция, превращающаяся в высказывание со значениями истина или ложь при фиксировании аргумента, называется предикатом. Тогда высказывание о любом предмете из данной предметной области будет предикатом P(x).

В общем, 1-местный предикат – это 1-местная логическая функция, при фиксировании аргументов которой получается высказывание.

Если P(x) – предикат, тогда:

– ?xP(x) означает то, что для всех x из области определения P(x) последний истинен, и называется квантором общности,

– $xP(x) означает то, что существует хотя бы одно значение x из области определения P(x), где P(x) истинен, и называется квантором существования.

Если A – формула логики предикатов, то область определения кванторов ?xA и $xA есть сама формула A.

Переменная x связанно входит в формулу A, если она является переменной кванторов ?x, $x или входит в область определения этих кванторов. Говорят, что x – связанная переменная. Иначе, x имеет свободное вхождение и называется свободной переменной.

В общем случае выражение вида ?xi1, xi2, ..., xir A(x1, x2, ..., xn), где xi1, xi2, ..., xir – подмножество множества x1, x2, ..., xn, понимается как утверждение, что для всех xi1, xi2, ..., xir из области определения A истинность A зависит только от свободных переменных.

Аналогично, выражение вида $xi1, xi2, ..., xir A(x1, x2, ..., xn) понимается как утверждение, что существует хотя бы один способ замены xi1, xi2, ..., xir своими значениями, при котором истинность формулы A зависит только от свободных переменных, входящих в эту формулу.

Справедлива двойственность кванторов общности и существования:

¬?xP(x) = $x ¬P(x), ¬$xP(x) = ?x ¬P(x),

где ¬ – операция отрицания.

Пусть x1, x2, ... – предметные переменные, a1, a2, ... – предметные константы, 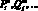– предикатные символы, – функциональные символы, где n, m – местность предикатов или функциональных символов.

Введя понятие терма и атома, можно определить формулу логики предикатов.

Терм:

1) любая xi есть терм;

2) любая ai есть терм;

3) если – функциональный символ и t1, t2, ..., tn – термы, то 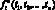– терм;

4) других правил образования термов нет.

Атом (элементарная формула):

1) любое переменное высказывание есть атом;

2) если 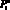есть предикатный символ и t1, t2, ..., tn – термы, то 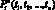есть атом;

3) других атомов нет.

Формула логики предикатов:

1) любой атом есть формула,

2) если A, B – формулы логики предикатов и x – предметная переменная, то ¬A, ¬B, A•B, A?B, A ~ B, A > B, ?xA, ?xB, $xA, $xB есть формулы. При этом •, ?, ~, > – соответственно операции конъюнкции, дизъюнкции, эквивалентности и следования,

3) других формул нет.

Формулы исчисления предикатов имеют смысл, если введена интерпретация. Под интерпретацией исчисления предикатов понимается система, состоящая из некоторого непустого множества D – области интерпретации и соотношения, относящего каждому предикатному символу 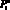некоторое n-местное отношение в D, каждому функциональному символу – n-местную функцию, отображающую Dn > D, и каждой константе ai – конкретный предмет из D. Предполагается, что предметные переменные пробегают область D, а логическим связкам придается обычный смысл.

Различают следующие формулы логики предикатов:

– высказывание как формула, не имеющая свободных переменных (замкнутая формула);

– формула со свободными переменными как отношение при одних значениях переменных может быть истинной, а при других – ложной;

– общезначимая формула (эквивалент тавтологии в исчислении высказываний), истинная при любой интерпретации;

– противоречивая формула (противоречие), ложная при любой интерпретации;

– выполнимая формула, истинная хотя бы при одной интерпретации.

Формула A(x), зависящая не только от x, свободна для переменной y, если никакое свободное вхождение переменной x не оказывается в области действия кванторов ?y или $y. Например, выражение A(x) = P(x, y)??yQ(y) свободно для переменной y, а формула
A(x) = P(x, y)??yQ(x, y) не свободна для переменной y, так как x входит в область действия квантора общности.

Обычно используются такие подстановки y вместо x, когда формула A(x) оказывается свободной для переменной y, то есть подстановка сохраняет связанные и свободные переменные.

Общая значимость формулы сохраняется при подстановках любой формулы, например, ??xA(x) > A(y) (^ – символ выводимости).

Нетрудно показать, что, если x – предметная переменная, B – формула, не имеющая свободного вхождения переменной x, то:

1) если общезначима B > A(x), то есть ^B > A(x), то общезначима и B > ?xA(x), то есть ^B > ?xA(x),

2) если ^A(x) > B, то ^$xA(x) > B.

Отсюда можно показать, что если ^A(x), то ^?xA(x). Действительно, если ^A(x), то для любой формулы B выводимо: если B ^ A(x), то ^B > A(x) или ^B > ?xA(x), или B^?xA(x), то есть ^?xA(x).

На основании введенных представлений задается формальная система FS2 исчисления предикатов первого порядка следующим образом.

Во-первых, определяется множество {T} исходных данных:

– x1, x2, ... – счетное множество предметных переменных;

– a1, a2, ... – счетное множество предметных констант;

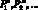–  – счетное множество предикатных символов;

–  – счетное множество функциональных символов;

– ¬, •, ?, ?, $ – операции и кванторы.

Во-вторых, задаются правила {?} конструирования правильно построенных фраз (ППФ):

– все атомы суть ППФ;

– если A, B – ППФ, x – предметная переменная, то ¬A, ¬B, A•B, A?B, A > B, ?xA, ?xB, $xA, $xB,– тоже ППФ;

– других правил конструирования ППФ нет.

В-третьих, вводится система аксиом {A}:

1) A > (B > A),

2) (A > (B > C)) > ((A > B) > (A > C)),

3) A•B > A ,

4) A•B > B,

5) (A > B) > (A > C) > (A > (B•C)),

6) A > A?B ,

7) B > A?B,

8) (A > C) > ((B > C) > (A?B > C)),

9) (A > B) > (¬B > ¬A),

10) A > ¬ ¬A,

11) ¬ ¬A > A,

12) ?xA(x) > A(y),

13) A(y) > $xA(x).

В-четвертых, определяются следующие правила вывода {B}:

1) все аксиомы выводимы (кем-то);

2) правило подстановки: допускаются только такие подстановки термов t1, t2, ..., tn вместо переменных x1, x2, ..., xn формулы A(x1, x2, ..., xn), для которых формула A свободна (для термов t1, t2, ..., tn), то есть допускаются такие подстановки, которые не изменяют связность и свободность переменных;

3) правило заключения (Modus Ponens): если ^A, ^A > B, то ^B;

4) правило обобщения (связывания квантором общности): если x – предметная переменная и B – формула, не содержащая свободного вхождения x, то если ^B > A(x), то ^B > ?xA(x) ,

5) правило конкретизации: если x – предметная переменная и B – формула, не содержащая свободного вхождения x и ^A(x) > B, то ^$xA(x) > B;

6) правило переименования связанной переменной: любая связанная переменная может быть заменена любой другой, отличной от свободной;

7) других правил вывода нет.

Система FS2 есть четверка {T, ?, A, B}.

В исчислении предикатов первого порядка переменной является некоторая предметная переменная x. В исчислениях предикатов более высоких порядков переменными являются предикаты P.

Отметим, что выводимые ППФ есть теоремы с применением {?, A, B} и посылок. Выводимость B из посылки A(A^B) означает следующее:

1) если A^A, то ^A > A;

2) если A^B1 и A^B1 > B2, то A^B2;

3) все выводимые в FS2 правильно построенные фразы выводимы также из A;

4) если B1 > B2(x) выводимо из A(A^B1 > B2(x)) и B1, и A не содержат свободного вхождения переменной x, то A^B1 > ?xB2(x) ;

5) если A^B1(x) > B2(x) и B2 и A не содержат свободного вхождения переменной x, то A^$xB1(x) > B2;

6) если A^B, то B, полученное переименованием связанных переменных, также выводимо из A;

7) если A^B, то B, полученное переименованием свободных переменных, отличных от связанных, тоже выводимо из A.

Аналогично трактуется выводимость из n гипотез (посылок). Результатом вывода является теорема.

Принцип резолюции Робинсона[105] позволил формализовать процесс доказательства теорем. Полнота исчисления предикатов первого порядка FS2 в широком смысле определена теоремой Геделя: любая общезначимая формула является теоремой.

Предикатами характеризуют классы ситуаций или отображают цели функционирования управляемых объектов. Во многих случаях управление большими системами представляется процессами построения предикатов формирования оптимальных отношений между частями (объектами) и т.д. и т.п.

Нечеткие отношения[106]. Известно, что лингвистической называют переменную, если ее значениями являются слова, фразы естественного языка. При этом лингвистическая переменная может быть описана набором (X, T, U, G, M), где X – название переменной; T – терм-множество переменной X, то есть множество всех названий лингвистических значений переменной X, причем каждое из таких значений является нечеткой переменной X со значениями из универсального множества U с базовой переменной u; G – синтаксическое правило, порождающее названия X значения переменной X; M – семантическое правило, которое ставит в соответствие каждой нечеткой переменной X смысл M(X).

Конкретное название X, порожденное синтаксическим правилом G, называется термом.

В свою очередь, нечеткое подмножество M определяется как некоторое множество в X с функцией принадлежности ?M(X), принимающей значения из интервала [0, 1]:

,

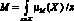где ?M(X): X > [0, 1]: – функция принадлежности.

Для каждого терма из терм-множеств, определенных для лингвистических переменных, строится соответствующее нечеткое множество M со своим носителем, определяемым на основе изучения экспертных оценок. При этом под носителем нечеткого множества понимают множество X? такое, что:

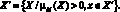
На следующем этапе строится набор правил, описывающих технологический процесс. Правила имеют вид: ЕСЛИ A = N, ТО B = M, где A, B – лингвистические переменные; N, M – термы соответствующих лингвистических переменных.

На основе набора правил строится матрица нечетких отношений. Как известно, нечеткое бинарное отношение R есть подмножество декартова произведения X?Y:

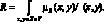
Далее построенные матрицы объединяются:

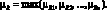
Для организации логического вывода используется композиционное правило логического вывода, частным случаем которого является известный силлогизм Modus Ponens:

посылка 1: ЕСЛИ x есть A, ТО y есть B;

посылка 2: x есть A;

вывод: y есть B.

Композиционное правило Л. Заде утверждает, что композиция нечетких отношений R(u) = A, R(u, v) = F есть R(v) = A0F, где 0 – знак композиции. При этом функция принадлежности определяется как:

Известны[107] примеры нечетких отношений, которые также полезно использовать в композиционных правилах вывода.

Несмотря на методологическую ясность и строгость формальных построений, отмеченное направление по формализации знаний и оперирования с ними для решения задач управления имеют две принципиально важные особенности:

– при базировании на исчислении предикатов FS2, по-видимому, останется принципиально неразрешимой проблема перевода фраз естественного языка;

– при использовании нечетких отношений врядли возможно получение и построение адекватных, соответственно, экспертных оценок и функций принадлежности (то есть построение адекватного многообразия нечетких множеств M со своими носителями).

Кроме того, касаясь языковых средств реализации[108], таких, как ПРОЛОГ, нечеткий ПРОЛОГ, MYCIN, PILOTEX, RTIME, ON и др., можно заметить, что они либо не допускают неопределенностей, либо допускают только одну из них, либо не работают в реальном времени. Наиболее подходящими формальными (языковыми) средствами реализации «идеологии» нечетких отношений в настоящее время, по нашему мнению, являются операторные схемы нечетких алгоритмов (ОСНА)[109]. Но и их применение в большей степени напоминает искусство, чем формализм моделирования.

Контрольные вопросы по лекции 11:

1. Поясните мысль о том, что концептуальная модель является начальной моделью только в системном плане.

2. Поясните, почему концептуальная модель – это некоторое представление знаний.

3. Легко ли построить пример, показывающий затруднения в процессе перевода фраз естественного языка в конструкции исчисления предикатов?

4. Какая особенность использования нечётких отношений ограничивает возможности их применения для формирования концептуальных моделей?