Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

СИСТЕМНЫЙ АНАЛИЗ (начальные понятия)

Раков В И,

Лекция 13. Языки представления знаний (логические и реляционные языки)

Известны три основные группы языков представления знаний ЯС: логические языки, реляционные языки и ролевые фреймы. Каждая имеет свои преимущества при удовлетворении требований, предъявляемых к языкам смысла [см. лекцию. 12].

Логические языки[114]. В первую группу входят логические языки, использующие для своего определения формальную систему логического типа: исчисление высказываний, исчисление предикатов первого порядка, многозначные логики или модальные исчисления. В любом случае, постулируется то, что в основе логического языка лежит некоторая фиксированная формальная система. Задается произвольное множество элементов, называемых термами: T = {t1, t2, ..., tn, ...}. Предполагается существование процедуры Q, которая эффективно определяет принадлежность некоторого элемента t множеству T и отождествляет его (если t ? T) с одним из элементов T. Кроме того, для любой пары элементов из T процедура Q определяет их совпадение. Природа термов может быть произвольной. В качестве ti могут выступать, например, буквы (графемы) русского алфавита, отдельные слова языка, иероглифы и т.п.

Определяются правила P, с помощью которых можно образовывать из термов некоторые совокупности. Все множество совокупностей, получаемых из T с помощью правил P, называют синтаксически правильными, а сами правила P – синтаксическими правилами. Правила P должны быть построены таким образом, чтобы существовала разрешающая эффективная процедура ?, которая позволяла бы для любой совокупности термов ? определять принадлежность ? к ?, где ? – множество всех совокупностей термов, получающихся из T с помощью P.

Выделяются в ? произвольным образом ?*?? и элементы ?* называют априорно осмысленными (аксиомами). Задаются правила Q, с помощью которых из одних элементов множества ? можно получать другие элементы множества ?. Эти правила называют семантическими правилами или правилами вывода. Как и для синтаксических правил, для правил Q должно выполняться условие, что они позволяют построить эффективную разрешающую процедуру ?, посредством которой для любой совокупности термов, входящей в ?, можно определить принадлежность этой совокупности к подмножеству ?**, где ?** [рис. 33] образуется при всевозможных применениях правил вывода к элементам подмножества ?*.

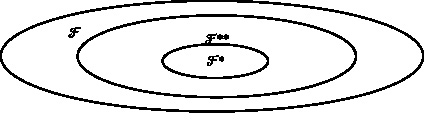
Рис. 33. Аксиомы и правила

Формальной системой называют четвёрку:

M = <T, P, ?*, Q>,

а эффективной формальной системой – семёрку:

Mэ = <T, Q, P, ?, ?*, Q, ?>.

Примерами подобных формальных систем могут служить исчисление высказываний или грамматики Хомского. В случае исчисления высказываний множество термов может быть задано в виде множества прописных латинских букв с произвольными целочисленными индексами. Синтаксические правила позволяют образовывать из этих термов правильно построенные формулы, и процедура ? есть процедура проверки соответствия правил P записи этих формул. В качестве аксиом можно использовать некоторый набор правильных формул и задать конечный набор правил вывода для них. Тогда получится формальная система (хотя, может быть, и не эффективная).

В случае грамматик Хомского, словари термальных и нетермальных символов образуют множество T, правила P задаются операцией приписывания, позволяющей образовывать из термов слова различной длины. Процедура ? есть простая проверка вхождения в слово элементов только из T. Она работает совместно с процедурой Q. В грамматиках Хомского система аксиом обычно содержит одну фиксированную аксиому S (специальный терм из нетермального словаря), а правила вывода задаются системой подстановок.

С формальными системами связывается такое понятие, как интерпретация. Для нее задается множество Z и специальная процедура ?, позволяющая отображать элементы множества ? на множество Z при условии, что задано отображение множества T для термов, входящих в интересующую совокупность из ?, на Z. Это отображение задается некоторой процедурой c, реализация которой происходит вне воли человека-исследователя. В классическом логическом исчислении в качестве Z используется двухэлементное множество {истина, ложь}. Наличие процедуры ? в этих исчислениях позволяет для каждой правильно построенной формулы при заданной интерпретации входящих в нее термов получить интерпретацию всей формулы. Например, для формулы 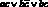, если a и b интерпретируются, как истина, а c – как ложь, интерпретацией всей формулы является истина.

В классическом логическом исчислении множество ?* выбирается таким образом, что интерпретация формул из ?* не зависит от интерпретации входящих в них термов. То есть при любой интерпретации входящих в них термов сами формулы интерпретируются однозначно. Правила вывода выбираются так, чтобы их применение не нарушало интерпретацию формул. При выполнении подобных условий становится возможным построение эффективной процедуры ?. Для классического исчисления высказываний выбирают в качестве аксиом только тождественно истинные формулы. Тогда, если правила вывода выбраны подходящим образом, множество ?** содержит лишь тождественно истинные формулы. Если при этом множество аксиом таково, что для этих правил вывода оно порождает все допустимые в данной системе тождественно истинные формулы, то процедура ? сводится к проверке тождественной истинности той формулы, чья принадлежность к ?** исследуется.

В известных версиях языков логического типа используется либо исчисление высказываний, либо исчисление предикатов первой степени. Выбор именно таких формальных систем обусловлен тем фактом, что для этих исчислений построены эффективные процедуры ?. Для более сложных формальных логических систем подобные построения сомнительны. Показано, что уже для исчисления предикатов второй степени построение такой эффективной процедуры принципиально невозможно.

Интересна особенность записей на предикатном языке. Если произвести обратный перевод, то есть перейти от предикатной записи к тексту на естественном языке, то могут получиться несколько иные тексты. Это означает, что при переводе с естественного языка на предикатный язык оба текста должны либо превратиться в одну и ту же предикатную запись, либо в записи, эквивалентные с точки зрения исчисления предикатов. Если исчисление предикатов выступает в качестве языка смыслов, то необходимо уметь организовывать процедуры отождествления различных синтаксических текстов, обладающих одинаковым смыслом.

Пусть H – множество трансформационных преобразований над предложениями естественного языка. Каждое преобразование меняет синтаксис предложения, но не меняет его смысл. Если N – совокупность всех предложений, получающихся друг из друга с помощью преобразований из H, то при переводе предложений из N в предикатные представления будут получаться различные записи. Для их преобразований друг в друга пользуются системой эквивалентных преобразований E, имеющейся в исчислении предикатов первого порядка:

1) f*? ? ?*f, где «?» есть &, V или ?;

2)  , где ? есть & или V;

3) 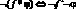, где ? есть & или V, а ° есть соответственно V или &;

4) ;

5) ;

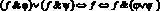6) 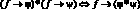, где «?» есть & или V;

7) ;

8) 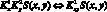, где и 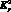 – одноименные кванторы;

9) ;

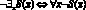10) 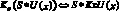, где K – произвольный квантор, S – формула, не зависящая от x, символ ? есть &, V или >;

11) , где U есть формула, не зависящая от x;

12) ;

13) Введение и элиминирование предметных областей. Это преобразование основано на том, что любые предметные области могут быть заменены на предметную область «предмет». Например, высказывания: «Сумма двух нечетных чисел есть четное число» и «Предмет, являющийся суммой двух предметов, каждый из которых есть нечетное число, есть четное число» имеют одинаковый смысл;

14) Квантор $x ? 1 может быть замещен на квантор $x. Это следует из того, что высказывания типа: «Существует по крайней мере один x такой, что...» и «Существует такой x, что...» по смыслу совпадают.

Сформулированные схемы преобразований 1-14 образуют систему E. Пусть имеем некоторое предложение естественного языка ?. Через N? обозначим множество всех предложений, получающихся в этом естественном языке из ? с помощью трансформационных преобразований из H. Предположим, что процедура перевода, имеющаяся в некоторой диалоговой системе, преобразует ? в предикатную формулу S?. Применим к S? всеми возможными способами преобразования из E. Пусть L? есть множество предикатных формул, полученных в результате этой процедуры. Формальная система будет эффективной, если все предложения из N? отображаются на семантическом этапе в формулы из L?, а предложения, не принадлежащие N?, не отображаются в формулы из L?. Ответ на вопрос о справедливости данного утверждения связан с аналитической оценкой множества H, то есть с анализом полноты системы трансформационных преобразований.

В целом языки ЯС логического типа не обладают мощными изобразительными возможностями для передачи всех оттенков и тонкостей смысла естественных языков. В предикатных языках невозможно выразить многие квантификаторы естественных языков такие, как только, как правило, много, изредка и т.п. Надо всегда точно указывать область действия предиката, что сужает набор текстов на естественном языке, для которых имеется полная аналогия с предикатным представлением. Необходимо значительное количество различных предикатов для использования. Анализ показывает, что мощность этого множества может совпадать по порядку с мощностью словаря языка и т.д. Однако несомненным преимуществом языков логического типа является способность этих языков к построению эффективной системы эквивалентных преобразований выражений.

Реляционные языки[115]. Вторую группу языков представления знаний составляют так называемые реляционные языки. В них вводятся конечные множества бинарных отношений R, с помощью которых передаются смысловые связи между элементами языка. Геометрической моделью для записей в реляционных языках служат семантические сети. Вершины в этих сетях отождествляются с элементами языка, дуги – с бинарными отношениями, существующими между этими элементами. Обычно рассматриваются языки, в которых априорно задаются конечные множества элементов языка X и конечное множество R. Такие (X, R)-языки выражают часть возможностей естественных языков и, как показывает практика, оказываются вполне пригодными для профессионально ориентированных систем. Математической моделью реляционных языков является алгебраическое понятие модели с носителем X и сигнатурой R. Теория таких моделей рассматривается в качестве теории реляционных языков. Вариант такой теории сформулировал Кодд.

Для языков этой группы характерно явное выделение отношений, связывающих между собой различные понятия. Распространены три языка: табличные языки Кодда, RX-коды и язык ситуационного управления.

Описание посредством языков Кодда осуществляется следующим образом. Текст на естественном языке вводится в память ЭВМ структурировано в виде таблицы (назовем ее для определенности таблицей Кодда). Каждая строка таблицы задается в виде некоторого фиксированного вектора:

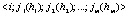(8)

где

1. i соответствует имени типа сущности. Например, в таблице – это левый столбец, в котором перечислены представители некоторого однородного множества. Сама таблица определяет тип сущности (штатный список работающих в настоящее время на предприятии, комплектность автомобиля, список обязательных товаров и т.п.). Например, если это штатный список работающих на предприятии, то левая колонка таблицы может быть перечнем (ФИО) людей, работающих в данный момент на предприятии.

2. jk являются именами атрибутов. Например, в случае штатного списка работающих это может быть пол, год рождения, специальность и т.д.

3. hk составляют значения атрибутов. В каждой строке таблицы конкретно по каждому работающему указываются его пол, год рождения, специальность, семейное положения и т.п.

Представления в виде (8) дают возможность человеку задавать вопросы диалоговой системе относительно имен, сущностей и атрибутов, а также о значениях атрибутов. Этим самым может быть обеспечено, с одной стороны, удовлетворение потребностей человека в требуемой для него информации, с другой – диалоговое заполнение таблицы или, другими словами, диалоговое формирование текста на естественном языке в памяти ЭВМ. Например, при наличии в памяти таблицы как множества векторов (8) можно сформулировать диалоговой системе следующие четыре вида запросов:

1) < ?; пол (ж); год рождения (1952); специальность (токарь) > ;

2) < ?; пол (м); год рождения (?); специальность (слесарь) > ;

3) < Смирнов Илья Ильич; ?1 (?); ?2 (?); ...; ?k (?) > ;

4) < ?; пол (м); год рождения (?); специальность (токарь) > .

Первый вопрос трактуется как вопрос об имени сущности, которая является женщиной 1952 года рождения и имеет специальность токаря. Простая процедура поиска по совпадению всех данных, имеющихся в запросе, приводит к тому, что диалоговая система в качестве ответа выдает текст: Родина Анна Петровна [табл. 4]. Второй запрос содержит специальную переменную ?. Ее смысл в указании на незначимость значения атрибута «год рождения». То есть от диалоговой системы требуется перечислить всех мужчин-слесарей, не обращая внимания на их возраст. В третьем запросе указано имя сущности, а на остальных местах стоят ?i(?) и k не фиксировано. Суть этого запроса может быть передана словами: «Сообщите все, что знает система о Смирнове Илье Ильиче». В четвертом запросе два вопроса, которые можно интерпретировать как «Укажите имена сущностей и годы их рождения для всех токарей мужчин». На этот запрос в нашем конкретном случае система должна ответить, что таких сущностей она не знает.

Таблицы Кодда формально задают на множестве H = I?H1?...?Hk, где Hi – множество значений атрибута ji, I – множество имен сущностей (l-арные отношения при l ? k). Они могут быть сведены к совокупности бинарных отношений с определенной потерей наглядности некоторой части сведений, содержащихся в таблице (например, [рис. 34]). Бинарные отношения отражают связи между сущностями и значениями атрибутов. Сами атрибуты при этом начинают играть роль бинарных отношений. В данном случае ? – иметь имя, r? – иметь пол, r? – родиться в, r? – иметь специальность. Если в вершину дерева поместить не сущность, а, например, специальность, то дерево перестроится и будет иметь другой вид, и отношения будут трактоваться по другому.

Таблица 4

Пример табличного языка Кодда

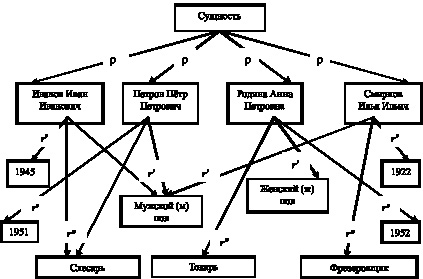
Рис. 34. Бинарные отношения между сущностями и значениями атрибутов

Для отношений можно построить алгебраическую теорию реляционных представлений. Эта теория позволяет строить не совокупность отдельных представлений, а единое алгебраическое представление для таблицы в целом. В рамках общей теории удается ввести над представлениями обычные алгебраические операции типа пересечения, объединения и дополнения, ставить задачу эквивалентных преобразований и т.д. Другими словами, удается создать специальные табличные реляционные языки, которые и именуются табличными языками Кодда. Можно показать, что эти языки эквивалентны языку исчисления предикатов первого порядка.

Естественным расширением возможности таких языков являются языки, в которых отношения заданы в явной форме. Такие языки получили название языки RX-кодов. Они используются в информационно-поисковых системах, где родовидовые отношения играют существенную роль. Выделим два типа объектов: предметы (X) и отношения (R). В качестве правильных синтаксических выражений будем использовать пары 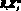, любые конъюнкции эти пар и конъюнкции, получающиеся при замене любого элемента Xj в правильном синтаксическом выражении на правильно построенное выражение. Пусть эти правила есть синтаксические правила языка.

Будем жестко приписывать предметам и отношениям некоторые семантические значения. В этом случае оказывается возможным производить определение новых понятий через ранее определенные, которые для этого нового понятия выступают в роли определяющих признаков.

Пусть, например, R1 есть отношение быть элементом класса, R2 – включать в качестве своего элемента. Пусть также 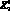– летательный аппарат тяжелее воздуха, 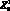– двигатель, создающий тягу и  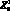– крыло. Тогда запись 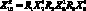дает определение предмета
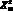, которое в словесной форме выглядит так: летательный аппарат тяжелее воздуха, включающий в себя крыло и двигатель, создающий тягу. Это определение можно рассматривать как определение понятия самолет.

Сами понятия 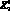, 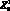и 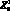 можно также задать в виде некоторых записей, представляющих собой правильно построенные выражения. Пусть 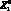– понятие летательный аппарат, 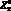– аэродинамическая сила, отношение R3 – использовать свойство. Тогда 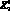может быть определено как 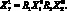Если X0 – силовая установка, 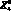– тяга, R4 – отношение давать, то 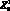можно определить как 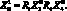Если, наконец, 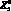– это неподвижная относительно целого несущая поверхность, – подъемная сила, то определение понятия крыло можно дать в следующей форме: 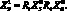Подставляя в определение самолета вместо соответствующих понятий их определения, получаем определение самолета через совокупность более частных признаков:

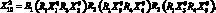(9)

Смысл верхних индексов заключен в том, что они показывают уровень обобщения понятия, позволяют вводить иерархию понятий и их классификацию. Естественная иерархия, присущая языку RX-кодов, позволяет эффективно организовывать поисковые процедуры. Однако у RX-кодов естественные ограничения: они хорошо описывают лишь древовидные структуры связей. Определяемое понятие должно быть корнем этого дерева, а связи между понятиями одного уровня не учитываются.

Для текстов на естественном языке древовидные структуры отношений не совсем типичны. В общем случае системы отношений образуют произвольную сеть, в которой могут встречаться циклы любого ранга, содержащие произвольное конечное число отношений. Поэтому естественным расширением возможностей языков типа RX-кодов явились языки синтагматических цепей. Примером такого языка является язык ситуационного управления.

Вводится множество термов, состоящее из трех классов: класс понятий X = {x1, x2, ..., xn, ...}, класс имен I = {i1, i2, ..., im, ...} , класс отношений R = {?, r1, r2, ..., rk}. Классы понятий и имен считаются конечными или счетными, класс отношений – конечным. Отношение ? играет роль отношения иметь имя. С помощью синтаксических правил из этих термов образовываются правильно построенные выражения. Элементарным выражением такого типа являются тройки (xirjxw), (xi?iw), (rj?iw), где xi ? X; iw ? I; rj ? R. Для образования более сложных выражений допускается введение операций конъюнкции, дизъюнкции и отрицания между элементарными выражениями. Операция отрицания может быть использована и для элементов из R.

Например, пусть X = {x1, x2}; I = {i1, i2, i3}; R = {?, r1, r2} Тогда образовываются элементарные выражения (x1r1x2), (x1?i3), (r2?i1) и более сложные выражения, такие, как:

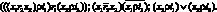
В первом их них путем суперпозиции произведена операция объединения нескольких элементарных выражений в сложное. Во втором – между двумя элементарными выражениями имеется операция конъюнкции и использованы операции отрицания над отношением r2 и элементарным выражением (x1?i3). В третьем выражении использована операция дизъюнкции.

В отличие от RX-кодов, язык ситуационного управления позволяет описывать не только постоянные отношения, присущие данному предмету, но и ситуативные отношения между предметами. Пусть имеется текст, описывающий определенную ситуацию: «Иванов сидит в кинотеатре «Восток» в 5-м ряду, занимая второе место. В этом же ряду на одиннадцатом месте сидит Петров, а сзади, за ним, Сидоров». Вводятся обозначения: x1 – человек, x2 – кинотеатр, x3 – местоположение, i1 – Иванов, i2 – Петров, i3 – Сидоров, i4 – «Восток», i5 – второе место пятого ряда, i6 –одиннадцатое место пятого ряда, i7 – одиннадцатое место шестого ряда, ? – иметь имя, r1 – одновременно, r2 – находиться в, r3 – занимать, r4 – быть непосредственно сзади. Тогда ситуация, описанная текстом, на языке ситуационного управления представится в виде:

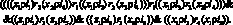(10)

В приведенной записи одновременно использованы отношение r1 и операция конъюнкции. Эти два средства выражения в языке ситуационного управления практически эквивалентны. Вместо приведенной в этой записи части, относящейся к фиксации местоположения Сидорова как сидящего непосредственно за Петровым, можно в явной форме указать его местоположение, используя имя i7.

Особенностью языков синтагматических цепей является их способность вводить новые понятия за счет выделения типовой структуры отношений. Например, имеем следующую ситуацию. По улице движутся одна за другой пять однотипных грузовых машин. Пусть их номера i1, i2, i3, i4, i5. Обозначим: x1 – автомашина, x2 – тип автомашины, x3 – улица, x4 – направление, i6 – грузовая, ? – иметь имя, r1 – обладать, r2 – двигаться по, r3 – находиться, r4 – быть сзади, r5 – быть в ?-окрестности.

Следующие записи фиксируют существование автомашин с данными номерами: (x1?i1), (x1?i2), (x1?i3), (x1?i4), (x1?i5). Обозначим эти элементарные синтагматические цепи как ?1, ?2, ?3, ?4, ?5 . Пусть ?j есть (?jr1(x2?i6)), где j = 1, 2, 3, 4, 5, что означает, что автомашина с номером ij является грузовой. Вводится запись (?jr3(x3??)), описывающая утверждение о том, что грузовая машина с номером ij находится на улице с именем ?. Имя ? играет особую роль. В исходном тексте нет названия (имени) улицы, но из текста следует, что все пять машин движутся по одной улице. Для этого и вводится нефиксированное название улицы ?. Повторение ? во всех записях для ?j означает их движение по одной и той же улице. Эти последние записи обозначаются ?j. Рассматриваются записи: (?jr2(x2??)). Имя ? для направления играет такую же роль, что и имя ? для улицы. Повторение его в записях указывает на то, что все пять автомашин движутся в одном и том же направлении. Обозначим полученные записи, как ?j. Сформулируем две окончательные записи:

? = (?1r4?2) (?2r4?3) (?3r4?4) (?4r4?5);

? = (?1r5?2) (?2r4?3) (?3r5?4) (?4r5?5).

Тогда запись ? & ? есть полное описание ситуации. Пусть теперь значение j не фиксировано равным пяти, а задано в виде произвольного параметра q > 2. Пусть также номера автомашин ij не фиксированы, а являются свободными переменными именами ?j. Тогда запись ? & ? означает не какую-то фиксированную ситуацию, а более общее понятие, которое можно назвать «колонна грузовых автомашин».

При отображении текстов естественного языка множеств X, I, R недостаточно. В естественном языке имеются средства квантификаторы (например, сильно, редко, иногда, далеко и т.п.), модальности (желательно, необходимо, возможно и т.д.), императивы (стой, сделай и пр.), модификаторы, оценки и многое другое. Расширение реляционных языков за счет введения дополнительных выразительных средств приближает их возможности к языкам смыслов. Например, следующий текст: «Иногда при повышении давления в первичном реакторе необходимо понизить в нем температуру» может быть заменен записью: ((m1x1)r1(m2 x2)) ? K(x3p1(m1x1)), где x1 – реактор, x2 – давление, x3 – температура, r1 – обладать, m1 – первичный, m2 – повышенное,
p1 – понизить, K – иногда. При этом m1 и m2 являются модификаторами, приписываемыми понятиям. Они задают некоторые призначные (от слова признак) характеристики для понятий. В ряде случаев их можно рассматривать как имена, но это может привести к усложнению записи. Императив p1 и квантификатор K также являются новыми элементами в описании. Модальность необходимости понижения температуры задана специальным знаком ?.

Сравнивая между собой языки предикатного (логического) и реляционного типов, необходимо заметить следующее. Язык представления знаний ЯС требует наличия трех эффективных процедур: процедуры перевода с естественного языка на ЯС, процедуры обратного перевода и процедуры эквивалентных преобразований внутри ЯС. Для предикатных языков процедуры последнего типа известны. Они сводятся к построению логического вывода в рамках исчисления предикатов первого порядка. Существуют довольно мощные процедуры такого типа, самой известной из которых является метод резолюций. Для реляционных языков таких эффективных процедур нет. Однако реляционные языки, как правило, обладают одним качеством, не присущим предикатным языкам. Они допускают эффективные процедуры обобщения описаний и позволяют создавать иерархически организованные системы знаний.

Таким образом, реляционные языки по своей структуре значительно ближе к естественным языкам, чем логические языки. Это приводит к тому, что процедуры семантического этапа при переводе текстов на язык ЯС и обратного перевода получаются для этого случая более простыми, чем аналогичные процедуры для логических языков. Но с точки зрения эквивалентных преобразований в реляционных языках нет возможности построить систему процедур, относительно которых можно было бы, как это сделано для исчисления высказываний или исчисления предикатов, доказать ее полноту и эффективность.

Контрольные вопросы по лекции 13:

1. Что такое формальная система?

2. Как можно пояснить факт того, что эффективной формальной системой называют семёрку: Mэ = <T, Q, P, ?, ?*, Q, ?>?

3. Что такое интерпретация?

4. Какой смысл вкладывается в систему эквивалентных преобразований E?

5. Объясните понимание вектора (8).

6. Поясните цепочку (9).

7. Опишите построение (10).

8. Что такое язык Кодда?

9. Поясните рисунок 34.

10. Какова основная идея построения языков RX-кодов?

11. В чём заключен смысловой переход от RX-кодов к языкам ситуационного управления?

12. Как можно объяснить суть языка ситуационного управления?

13. Какое принципиальное отличие логических языков от языков реляционного типа?