Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

СИСТЕМНЫЙ АНАЛИЗ (начальные понятия)

Раков В И,

Лекция 19. Имитационное моделирование

Сложности моделирования (см. лекцию 17) локально организованной среды обусловлены:

– её изменчивостью: способствующие и препятствующие причины могут «меняться местами»,

– сложностью представления или описания (моделирования) функционирования интеллектуальных объектов сложной системы, то есть поведения людей в системе и среде,

– трудностями понимания, восприятия и описания локально организованной среды: отсутствие или неопределённость функциональных границ среды и объекта,

– сложностью оценки полноты знаний о содержательности локально организованной среды.

Множество подобных сложностей принципиально порождается одним фактором – невозможностью восприятия конкретного явления (объекта, процесса) вне той среды, в которой оно существует.

Человек воспринимает явления объективной реальности в виде некоторых психических образов, осмысление которых формирует некоторый мысленный образ (мысленную модель) явления объективной реальности. Именно с ним осуществляются мысленные эксперименты и проводятся различные умозаключения.

Как отмечалось, мысленные образы (исходного) явления – это симбиоз образов явления (системы) и среды. Соответствующие этим образам некие реальные объекты могут быть далёкими или близкими от реальных и среды, и исходного явления (системы) в силу следующих причин:

1) внешний мир имеет существенно большее число степеней свободы, чем человек с его пяти координатной чувственной сеткой, усиленной соответствующим приборным оснащением;

2) уровень внутреннего индивидуального «интеллектуального обеспечения» собственно человека, воспринимающего и представляющего явление объективной реальности, может иметь большее или меньшее соответствие исследуемым (воспринимаемым) обстоятельствам.

По-видимому, факт априорного вuдения, определения или установления «строгих» границ между явлением и средой можно считать нетипичным, нехарактерным или даже, попросту, невозможным. Тогда можно полагать, что образ явления как симбиоз (композиция, конгломерат) явления и его среды, воспринимаемый и осмысливаемый человеком, является исходным материалом при моделировании явлений объективной реальности. В таком случае и методика моделирования структур «объект-среда» должна соответствовать этой реальности. Базовую методологию такого моделирования составляют методы имитационного моделирования, ориентированные на воспроизведение и исследование «композиционных» образов явлений объективной реальности.

1. Понятие имитационного моделирования[138].

Идея, на которой основано имитационное моделирование, довольно простая. Если не удаётся построить математическую или статистическую модель объекта, то можно в памяти ЭВМ отобразить сам объект управления и протекающие в нём процессы.

Рассмотрим простой пример имитационного моделирования.

На рисунке [рис. 45] показана небольшая часть транспортных магистралей города, состоящий из четырёх регулируемых перекрёстков. Вдоль магистралей стрелками указаны направления движения транспорта.

Задача управления системой перекрёстков может быть сформулирована следующим образом: найти такое управление переключением светофоров на перекрёстках, которое обеспечивало бы минимизацию среднего времени ожидания транспорта, находящегося в границах управляемой зоны.

Управляемая зона ограничена некоторыми сечениями магистралей, которые обозначены буквами A, B, C, D, E, F, G [рис. 45].

В такой постановке, если известны вероятностные законы поступления автомашин в управляемую зону через сечения B, C, D, E, задача является типовой для теории массового обслуживания. Однако если поступление автомашин не описывается простейшими потоками (пуассоновскими), то её аналитическое решение в рамках теории массового обслуживания пока затруднено.

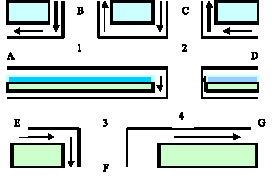
Рис. 45. Пример зоны управления транспортной магистрали города

Для этого примера переход к некоторой имитационной модели объекта управления проводится следующим образом. Эта модель носит название дискретной ситуационной сети (ДСС).

ДСС представляет собой ориентированный граф с вершинами четырёх типов, называемых истоками, стоками, пассивными и активными решателями.

Истоки характеризуются тем свойством, что они представляю собой вершину графа, в которой нет входящих дуг и имеется только одна выходящая дуга.

Стоки совпадают с вершинами графа, в которые входят несколько дуг, но не выходит ни одной дуги.

Остальные вершины графа относятся к решателям. Пассивным решателям соответствуют вершины, у которых имеется только одна входящая и одна выходящая дуга. Активным решателям – вершины с произвольным числом входящих и выходящих дуг (единственное ограничение – наличие хотя бы одной входящей и одной выходящей дуги).

Разница между пассивными и активными решателями – в их влиянии на функционирование ДСС. По ДСС могут перемещаться некоторые объекты, формально характеризуемые некоторыми наборами параметров 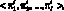(i – собственный номер данного объекта).

ДСС функционирует в дискретном времени с квантами величины ?t. В каждый фиксированный момент времени t все объекты находятся в истоках или решателях. Объекты, попавшие в некоторый момент времени в вершину-сток, исчезают из ДСС. В истоках объекты появляются в моменты времени t согласно некоторому детерминированному или вероятностному закону.

В пассивных решателях объекты задерживаются на некоторое детерминированное или вероятностное время, зависящее от характеристик объекта. Пассивные решатели выполняют в ДСС роль задержек.

В активных решателях объекты также могут задерживаться на детерминированное или вероятностное время. Кроме того, в них могут изменяться значения параметров объекта и выбираться новое направление перемещения объекта вдоль какой-либо дуги, выходящей из активного решателя.

На рисунке [рис. 46] показана ДСС, соответствующая системе перекрёстков [рис. 45]. Роль истоков играют сечения B, C, D, E , а роль стоков – сечения A, B, C, F, G . Поскольку сечения B, C одновременно играют роль истоков и стоков, то разобьём их на две составляющие, одну из которых будем сопоставлять с истоком, а другую – со стоком, определяемыми этими сечениями. На рисунке [рис. 46] истоки показаны в виде треугольников, а стоки – в виде квадратов.

Каждый перекрёсток в ДСС представляется активным решателем, отмеченным тем же номером, что и перекрёсток. Все магистрали, ведущие из истоков к перекрёсткам и от одного перекрёстка к другому, заменяются в ДСС пассивными решателями. Активные решатели [рис. 46] показаны кружками, а пассивные – маленькими прямоугольниками.

Функционирование этой ДСС опишем, предполагая, что при сборе информации проектировщику системы управления известны законы 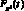, , 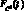FD(t) , FE(t) появления автомашин в истоках. Будем считать, что роль параметров для объектов-автомашин в нашей модели играют: ?1 – время нахождения в зоне управления, ?2 – время ожидания в активных решателях, накопленное за время нахождения объектов в зоне управления, ?3 – тип автомашины (обычный или специальный), ?4 – средняя скорость движения, ?5 – направление движения.

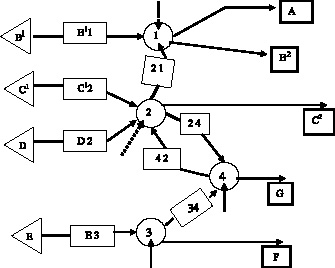
Рис. 46. Дискретная ситуационная сеть (ДСС)

Ситуацией на ДСС в момент времени t будем называть перечень объектов, имеющихся на ДСС в этот момент времени, набор значений параметров этих объектов и указание их местонахождения в вершинах ДСС. Ситуация в момент времени t обозначается как S(t).

В отличие от пассивных решателей активные решатели имеют дополнительный вход, по которому на них поступает сигнал управления. Этот управляющий вход показан пунктирными стрелками [рис. 46]. В нашем случае в качестве управляющего воздействия на активные решатели поступает команда о переключении светофора. Если исключить из рассмотрения случай подачи жёлтого сигнала по обоим направлениям (что совсем не обязательно для организации движения автотранспорта), то число различных управляющих воздействий, подаваемое на ДСС, будет равно 24.

Процесс имитационного моделирования системы перекрёстков с использованием построенной ДСС протекает в ЭВМ следующим образом. В начальный момент полагается t = 0 и задаётся случайное (или требуемое начальное) распределение объектов по пассивным решателям, а также случайное (или требуемое) распределение значений параметров у этих объектов (на рисунке [рис. 47] этим операциям соответствует блок Задание начальных значений). После этого в истоках, в соответствии с законами порождения, появляются автомашины, имеющиеся на границах управляемого участка в момент времени t = 0.

Далее начинает работать алгоритм перемещения объектов из пассивных решателей в активные. Суть этого алгоритма состоит в выработке условий перемещения каждой автомашины из пассивного решателя в активный, с которым его соединяет выходящая из пассивного решателя дуга. Условия перемещения определяются средним значением скорости, которую имел автомобиль при попадании в пассивный решатель, и предполагаемым временем, которое он затратит на прохождение магистрали на участке, имитируемом данным пассивным решателем. Предполагаемое время прохождения участка может однозначно определяться средней скоростью автомашины или некоторым вероятностным распределением времени, заданным для данного пассивного решателя.

Этим операциям соответствует блок «Заполнение активных решателей» [рис. 47]. Отметим, что при работе модели автомашин, которые в момент времени t = 0 появились в истоках, остаются пока в них, а те, которые должны перемещаться из пассивных решателей в активные, перемещаются в них.

После этого начинает работать блок «Заполнение пассивных решателей» [рис. 47]. Этот блок выполняет несколько функций:

1) все автомашины, которые бы появились в истоках в момент времени t = 0, перемещаются в те пассивные решатели, которые с ними связаны дугами,

2) в активных решателях происходит обработка автомашин, имеющихся в окрестности данного перекрёстка на основании алгоритма управления светофором, введенным в данный активный решатель. Если, например, этот алгоритм устроен так, что светофор на перекрёстке переключается через определенные временные кванты, то происходит проверка условия переключения светофора, и все автомашины, которые могут двигаться при реализуемом сигнале светофора, начинают перемещаться в стоки или соответствующие пассивные решатели.

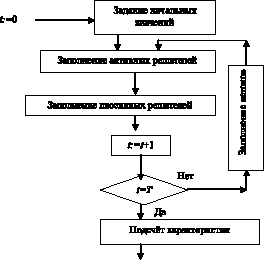
Рис. 47. Унифицированная блок-схема имитационного моделирования

Если из данного активного решателя выходит более одной дуги (более одного направления), то используется специальный механизм приписывания автомашинам, выходящим из активного решателя, направления дальнейшего движения. Кроме того, для автомашин, которые должны быть перемещены в стоки ДСС, производится анализ временных характеристик, а результаты этого анализа запоминаются.

На этом заканчивается один цикл работы модели. Далее содержимое счетчика времени моделирования увеличивается на единицу, что соответствует переходу от ситуации S(0) к ситуации S(1). Происходит проверка условия того, что моделирование закончено. В ЭВМ заранее вводится время T = q•t, где q – некоторое целое положительное число. Если время ещё не равно T, то начинает работать блок Заполнение истоков [рис. 47], который на границах зоны управления порождает в истоках потоки объектов с заданными характеристиками.

После этого происходит циклическое повторение описанного процесса.

После окончания цикла моделирования производится подсчет суммарных временных характеристик, с помощью которых оценивается эффективность выбранного в активных решателях управления. После анализа можно изменить алгоритм управления и вновь начать моделирование.

2. Возможности имитационного моделирования.

На описанном выше принципе работает большинство моделирующих программ, имитирующих процессы, протекающие в объекте управления. В частности, в качестве объекта моделирования может выступать и сама проектируемая система управления. В этом случае при моделировании можно изменять структуру этой системы, временные характеристики тех или иных подсистем, а также порядок работы.

Идея имитационного моделирования «позаимствована» из повседневной жизни, поскольку наши решения связаны с предварительным «проигрыванием» последствий принятия этих решений на какой-то модели жизненной ситуации.

Дискретные ситуационные сети (ДСС) – не единственная модель, которая может быть использована при составлении имитационных моделей, в частности, могут использоваться и модели проф. Д. Форрестера – так называемые модели имитационного динамического моделирования[139] в методе System Dynamics (Simulation Modeling). Также примером моделей другого типа могут служить модели, в которых в функции управления входит распределение ресурсов на сети в соответствии с некоторым заданным критерием. Однако для описания сущности процесса имитационного моделирования ДСС подходят как нельзя лучше.

У имитационных моделей есть одно принципиальное ограничение. Они являются пассивными моделями, для которых не требуется поиск управления, наилучшего с позиций некоторого критерия. В больших (сложных) системах проблема поиска управления не менее важна, чем проблема построения модели управляемого объекта управления.

Контрольные вопросы по лекции 19:

1. Почему структуры «объект-среда» являются базовыми структурами при организации деятельности сложных объектов?

2. Какова основная идея имитационного моделирования?

3. Приведите примеры использования имитационного моделирования при принятии решений в повседневной жизни.

4. Объясните рисунок 47.

5. Сформулируйте принципиальное ограничение имитационного моделирования.