Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

СИСТЕМНЫЙ АНАЛИЗ (начальные понятия)

Раков В И,

Лекция 24. Прогнозирование

Прогнозирование представляет собой научно обоснованное суждение о будущих состояниях объекта прогнозирования и (или) об альтернативных путях достижения этого состояния. Необходимость прогнозирования вызвана тем обстоятельством, что будущие состояния объекта имеют большое значение для решений, принимаемых в настоящий момент. Имеет место неопределенность, связанная с будущей ситуацией, которую полностью устранить невозможно. Основной задачей субъекта, принимающего решение при наличии неопределенностей, является нахождение оптимального решения из ряда альтернатив. Прогнозирование выступает как один из инструментов поиска такого решения, которое должно приниматься на основе научно обоснованного, объективного анализа проблемы.

С прогнозированием связывают два понятия: forecasting (прогнозирование) и prediction (предсказание). Глагол to predict означает сказать заранее, а глагол to forecast – бросать вперед. Можно предположить наличие «чего то», что можно было бы «бросить вперед». При прогнозировании роль этого «чего-то» выполняют имеющиеся сведения о процессе. Функция «бросить вперед» может отрабатываться в пространстве независимо от времени, во времени независимо от пространства, в очередности событий, ситуаций или обстоятельств независимо от времени и пространства и в более сложных композициях. Словом, там, где существуют, определяются или задаются некие «отношения порядка» (очередности, последовательности).

Р. Браун (1963)[187] использует понятие предсказание (prediction) для обозначения субъективных оценок будущего и понятие прогноз (forecast) для обозначения результатов объективных вычислений.

Д.М. Гвишиани и В.А. Лисичкин (1968)[188] определяют понятия предсказание и прогноз более прагматично. Предсказание – как предвидение таких событий, количественная характеристика которых либо невозможна (на данном уровне познания), либо затруднена. Про-
гноз – как высказывание, фиксирующее в терминах какой-либо языковой системы ненаблюдаемое событие и удовлетворяющее следующим условиям:

– в момент высказывания сомнительна возможность его истинности или ложности;

– оно содержит указание на пространственный или временной конечный интервал, внутри которого произойдет прогнозируемое событие;

– в момент высказывания необходимо располагать способами проверки метода прогнозирования, априорной оценки шансов появления прогнозируемого события и проверки осуществления прогнозируемого события.

Э. Янч (1974)[189]вкладывает в эти понятия несколько другое содержание: в прогноз (forecast) – вероятное утверждение о будущем с относительно высокой степенью достоверности; в предсказание (prediction) – аподиктическое (не вероятностное) утверждение о будущем, основанное на абсолютной достоверности. В общем, в ретроспективном плане понятия предсказание, прогнозирование и прогнозирующая система наделяются следующим смыслом. Под предсказанием обычно понимают искусство суждения о будущем состоянии объекта, основанное на субъективном взвешивании большого количества качественных и количественных факторов, под прогнозированием – некоторый исследовательский процесс, в результате которого устанавливаются возможностные (например, вероятностные) данные о будущем состоянии прогнозируемого объекта.

Прогнозирующая система, как правило, – это некая организационно-техническая система, обрабатывающая поступающие на вход данные о прогнозирующем объекте с целью получения на выходе данных о будущем состоянии этого объекта, то есть с целью получения прогноза.

Прогноз может быть качественным и количественным. Качественный прогноз можно получить как через цепь дедуктивных или индуктивных выводов, так и посредством количественного анализа. Количественный прогноз связан с «возможностями», с которыми происходит то или иное событие в будущем, а также с некоторыми количественными характеристиками этого события (например, его математическим ожиданием, наиболее вероятным значением и т.д.).

Различают участок наблюдения, где процесс изучается в течение некоторого времени, и точку упреждения, в которой оценивается как математическое ожидание процесса (точечный прогноз) и величина интервала, в который с заданной вероятностью попадет будущее значение процесса (интервальный прогноз).

Естественным требованием к качеству данных, полученных в результате прогнозирования, является их точность. Однако данные даже самых совершенных прогнозирующих систем могут совпасть с количественными данными об объекте в будущем лишь с некоторой вероятностью. Если неправомерно требовать точного совпадения величины прогнозируемого значения с его будущим значением, то вполне законным является требование попадания будущего значения в некоторую область значений, определяемую при прогнозировании. Прогнозирующая система, дающая меньшую величину области, в которой будет находиться будущее значение параметра объекта, обычно предполагается более точной (предпочтительной).

Важным требованием к изучаемой системе является способность к реагированию на изменения, происходящие в изучаемом объекте прогнозирования с целью устранения ошибок прогнозирования, которые могут быть вызваны следующими причинами.

Во-первых, существованием неопределенности будущей ситуации. При получении новой информации об объекте мы не можем с уверенностью сказать, что ошибка прогнозирования вызвана только влиянием неопределенностей, так же как это, например, имело место в предыдущих наблюдениях за этим объектом. Задачей прогнозирующей системы является максимальное уменьшение уровня неопределенности (например, фильтрация помех в технических системах).

Во-вторых, может возникнуть ситуация, когда ошибки прогнозирования вызваны изменениями в закономерностях функционирования самого объекта или изучаемого процесса. Прогнозирующая система должна как можно быстрее «распознать» это изменение и производить дальнейшее прогнозирование с учетом этого изменения.

Наконец, в-третьих, в самом общем случае ошибки прогнозирования вызываются одновременно теми и другими причинами, т.е. прогнозирующая система должна «уметь» своевременно отличать «полезные» изменения в объекте прогнозирования от результата влияния неопределенностей, уровень которых необходимо уменьшить. В системах управления эта задача аналогична задаче прогнозирования величины полезного сигнала при одновременном осуществлении фильтрации помех. Приведенные требования являются общими для любой прогнозирующей системы.

В некоторых случаях к прогнозирующей системе можно предъявлять и другие требования, вытекающие из специфики решаемой задачи. Например, требование повышения «быстродействия» при уменьшении интервала времени поступления информации, что происходит, например, в системах управления техническими объектами. В этом случае задачу прогнозирования можно решать только при применении ЭВМ. В некоторых случаях существенными могут являться требования простоты и минимальной стоимости получения прогноза.

1. Схема прогнозирования.

Любое прогнозирование строится на основе имеющейся информации об изучаемом объекте. Эта информация связана: с поведением данного объекта в прошлом и настоящем, с ранее установленными научными положениями о поведении подобных объектов в подобных ситуациях (прошлый опыт). Само «предвидение есть по своему существу операция над прошлым» (У. Эшби, [рис. 64])[190].

Возможны, вероятно, различные «операции» «над прошлым». В первую очередь, «прошлое» должно позволить найти общие закономерности (если таковые вообще имеются) в поведении подобных объектов в подобных ситуациях. Рубеж научного прогнозирования лежит там, где исчерпывается возможность обосновать развитие объекта, опираясь на эти закономерности.

Нахождение закономерности в поведении прогнозируемого объекта позволяет построить его математическую модель, которая вследствие возможности некоего морфизма позволяет исследовать реальные физические процессы путем их математического моделирования. На выбор модели оказывают влияние цель и задачи прогнозирования и величина того интервала, на который оно производится.

После выбора модели прогнозируемого объекта определяются ее неизвестные параметры. Затем производится прогнозирование состояния объекта в интересующий нас будущий момент времени, который может быть задан неявно, например, другой независимой переменной. При определении параметров модели, в частности, может эффективно использоваться метод наименьших квадратов.

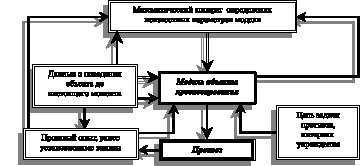
Рис. 64. Структурная схема прогнозирования, где: двойные стрелки – вычислительные операции; одинарные стрелки – исследовательские операции

При заданных цели прогноза и интервала упреждения условия получения точного прогноза могут обуславливаться следующими факторами.

Во-первых, имеющаяся информация об объекте прогнозирования должна соответствовать (или могла быть приведена к соответствию) цели и задачам прогнозирования. Например, информация о начальных условиях при прогнозировании траектории полета шарика должна быть выше по точности, чем требуемая точность прогноза. Очистка исходных статистических данных является важной и далеко не всегда тривиальной задачей. Даже при правильно выбранной модели и производстве всех вычислений с необходимой точностью, неочищенный статистический материал не позволит сделать хороший прогноз.

Во-вторых, выбранная модель должна правильно учитывать особенности функционирования объекта прогнозирования. Правильное выявление законов его развития является гарантией успешного выбора модели при прогнозировании. Любой закон, научная гипотеза или модель имеют определенную область применения. Границы этой области не всегда являются достаточно четко очерченными. При неправильном выборе модели или области ее применения сомнительно получение реальных результатов прогнозирования.

В-третьих, необходимым условием точности прогнозирования является правильный выбор метода идентификации неизвестных параметров модели. При выборе метода идентификации необходимо, как правило, учитывать: прошлый опыт работы с подобными объектами, результаты исследования поведения объекта прогнозирования в прошлом и настоящем, вид выбранной модели.

В-четвертых, прогнозирующая система не должна быть разомкнутой по отношению к получаемым результатам. Подвергаясь логическому анализу, результаты прогнозирования могут служить основой для внесения поправок и изменений в элементы прогнозирующей системы.

2. Моделирование и классификации.

Одним из важнейших этапов процесса прогнозирования является выработка модели изучаемого процесса[191]. Наиболее широко распространены математические модели, хотя в некоторых случаях успешно используются и физические модели (испытание модели летательных аппаратов в аэродинамических трубах, испытание макетов будущих плотин в специализированных лабораториях и т.д.). В целом, для представления проблематики прогнозирования является достаточной следующая трактовка модельных процессов.

Модель. Модель является представлением объекта, системы или понятия (идеи) в некоторой форме, отличной от формы их реального существования и служит средством для последующего объяснения, понимания или совершенствования.

В простейшем случае модель – это воспроизведение чего-либо. «В науке по ее существу всегда приходится иметь дело с моделями. Вне их конкретных классов бессмысленно говорить об основных понятиях теории и закономерностях природы»[192].

В прогнозировании принято различать натуральный объект или процесс – натуру, – и модельное отображение этого объекта или процесса – модель. Натура и модель находятся в определенном соответствии. Модель отображает натуру в плане конкретно поставленной задачи и неразрывно связана с целью исследований натуры.

Построение модели предполагает некоторое воспроизведение объекта с вполне конкретной целью. Рассматриваются только те его стороны, которые с достаточной для целей прогнозирования точностью описывают изучаемый объект. «Задача нахождения адекватных каждому уровню познания моделей и пределов их справедливости составляет основное содержание физических исследований и теоретического разрешения технических проблем»192.

Моделирование. По существу анализ объекта при прогнозировании – это анализ специальным образом построенных моделей. От того, насколько правильно построены отдельные модели, как они увязаны друг с другом, зависят результаты прогнозирования.

В основе математического моделирования лежит явление морфизма, который означает сходство форм при качественном различии явлений. В математике изучение, например, одной из изоморфных систем сводится в значительной степени к изучению другой изоморфной системы. Изоморфизм указывает на единство, связь, взаимодействие и взаимозаменяемость в определенных пределах различных явлений материального мира, на сходство их формы и отдельных закономерностей. Поэтому в строго определенных границах и условиях можно заменить изучение одного явления изучением другого, подобного ему по форме и структуре. Появляется возможность моделировать одну систему с помощью другой.

Функции модели. Различают по крайней мере пять ставших привычными случаев применения моделей в качестве средства понимания действительности, средства общения, средства обучения и тренажа, инструмента прогнозирования или средства постановки эксперимента.

При математическом моделировании вместо изучения и исследования оригинала исследуются математические зависимости, описывающие оригинал. Основное требование к математической модели состоит в необходимости учитывать основные стороны и взаимосвязи рассматриваемого явления и отказаться от изучения второстепенных сторон и связей. Таким образом, модель представляет собой некоторую абстракцию от действительности, учитывающую только характеристики, представляющие интерес. Может показаться, что рассмотрение в модели второстепенных сторон и связей может уточнить получаемый результат. Однако иногда это приводит лишь к усложнению модели и ухудшению результатов.

Трудности выбора и обоснования модели объекта прогнозирования представляют собой задачу, сложность которой зависит от ряда факторов:

– наличия и степени изученности процессов, подобных изучаемому,

– «степени искаженности» сведений о данном конкретном процессе,

– объема соответствующих сведений.

Различают модели детерминированных процессов при полной априорной информации об их параметрах. Известны также модели детерминированных процессов при неполной априорной информации о параметрах модели (неизвестны начальные условия при известных дифференциальных уравнениях, неизвестны некоторые коэффициенты дифференциальных уравнений и т.п.).

Если вид модели физического процесса априорно известен и информация о нем не является искаженной различными помехами, то при решении задачи прогнозирования обычно встречаются трудности лишь вычислительного характера. Если вид модели процесса априорно неизвестен, но процесс является детерминированным и информация о нем не искажена, задача прогнозирования, как правило, также может быть успешно решена.

Более сложную задачу представляет определение модели процесса при наличии ограниченной информации о нем, например, вида «процесс является стационарным», «такая-то характеристика процесса является неубывающей (не возрастающей) функцией времени» и т.п.

Наконец, в тех случаях, когда о процессе априорно ничего не известно и поступающая информация является искаженной различными помехами, задача выбора и обоснования модели такого процесса становится сложной и требует высокого индивидуального мастерства исследователя.

Классификация моделей. В зависимости от вида прогнозируемого объекта различают модели физических процессов; развития производства; развития науки и техники; экономические модели; демографические модели; социальные модели; модели политических ситуаций и т.п. К классификации моделей иногда рационально подойти с позиций классификации многообразия возможных задач, решаемых в процессе прогнозирования. Здесь выделяются два случая воспроизведения натуры: материальное (предметное) и идеальное (абстрактное) [рис. 65][193].

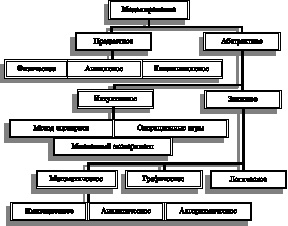
Рис. 65. Возможные виды моделирования

Материальное воспроизведение натуры предполагает исследование объекта на физических моделях, при котором изучаемый процесс (объект) воспроизводится с сохранением его физической природы или используются другие аналогичные физические явления. Натуральное моделирование – частный случай материального моделирования. Основное требование материального моделирования – соблюдение подобия оригинала и модели.

Абстрактное воспроизведение – это описание объекта определенными символами. Особое место в абстрактном воспроизведении играют математические модели, исследования в которых осуществляются на основе идентичности формы уравнений и однозначности соотношений между переменными, фиксируемыми в натуре и модели. В последнее время для решения трудно формализуемых задач большое значение приобретают методы эвристического (интуитивного) моделирования.

В зависимости от характера протекания прогнозируемого процесса существуют группы интуитивных моделей: эволюционного развития; революционного развития; «комбинированного» развития, включающего элементы и эволюционного, и революционного развития.

В зависимости от вида математического описания аналитические модели можно разделить на следующие группы: основанные на дифференциальных уравнениях процесса; основанные на алгебраических и трансцендентных уравнениях, связывающих прогнозируемую величину с рядом других величин.

В зависимости от наличия неопределенностей, сопровождающих прогнозируемый процесс, среди имитационных моделей можно выделить детерминированные и стохастические. Стохастические модели в свою очередь разделяют на модели:

– для расчета математических ожиданий процессов (модели динамики средних для массовых явлений в экономике, биологии, военном деле) в непрерывной или дискретной форме;

– вероятностные в непрерывной форме (теория массового обслуживания, стохастические дуэли и т.д.) или дискретной форме (марковские цепи);

– статистических испытаний (метод Монте-Карло).

В зависимости от вида функций, описывающих детерминированную основу процесса, аналитические модели могут быть: полиномиальные (и, в частности, линейные и квадратичные), тригонометрические, экспоненциальные, а также комбинированные, включающие различные комбинации перечисленных моделей.

Большинство из приведенных видов моделирования находит применение в задачах прогнозирования.

3. Скачки в развитии.

Как известно, прогноз методически должен предусматривать возможность определения как характеристик эволюционного развития, так и параметров так называемых «скачков», при которых происходят резкие качественные изменения. Необходимо требовать прогнозировать и моменты «перерыва постепенности», и характеристики процесса после осуществления такого перерыва. Развитие точных наук показывает[194], что имеется принципиальная возможность разработки количественных методов прогнозирования скачков в рамках общей модели изучаемого процесса.

Сама постановка такого вопроса применительно к математическим моделям, используемым для прогнозирования количественных характеристик процессов, приводит к выводу о необходимости применения методов исследования, способных анализировать топологическую структуру решений, предлагаемых моделью, которая применяется для описания процесса. К числу таких методов относятся теории устойчивости, инвариантности и бифуркаций[195].

Теория устойчивости строится с учетом действующих на объект внешних возмущений и позволяет определить пространство параметров управляющих воздействий, обеспечивающее устойчивую траекторию системы объект – внешняя среда, близкую к невозмущенной. Выход за границу устойчивости приводит к непредсказуемому поведению системы в рамках используемой модели. Стремление обеспечить ее функционирование в рамках определенной структуры может приводить в ряде случаев к формализации границы меры в виде уравнения, описывающего границу устойчивости.

Особый интерес представляет анализ поведения динамической системы после перехода через границу устойчивости, когда происходит изменение ее топологической структуры. Решением подобных задач занимается теория бифуркаций196. Начиная с работ А.А. Андронова и Л.С. Понтрягина введено понятие грубых и негрубых систем. Получены условия грубости и негрубости, которые позволяют анализировать топологическую структуру решений и определять, является ли система в принципе бифуркационной, т.е. меняет ли топологию решений в пространстве параметров. Таким образом, методы исследования динамических систем позволяют предсказывать скачки в их развитии и могут быть с успехом использованы при проведении прогнозирования на длительные сроки.

Другое направление, тесно связанное с понятием устойчивости, занимается исследованием условий, при которых выходные параметры системы не зависят (абсолютно или с заданной точностью) от влияющих на нее возмущающих воздействий. Формализация этих условий является предметом теории инвариантности, которая выделяет в классах управляемых систем магистральные траектории развития. Предполагается, что поведение сложных систем (экономических, биологических и т.д.) следует таким магистральным траекториям.

4. Подходы к прогнозированию.

Существует много способов прогнозирования[196]. Все они представляют три подхода к решению вопросов прогнозирования: эвристический, математический и комбинированный.

Эвристический подход имеет экспертную природу и основан на использовании мнения специалистов в данной области знания и, как правило, используется для прогнозирования процессов, при формализации которых встречаются значительные трудности.

Математический подход прогнозирования в зависимости от вида математического описания изучаемых объектов и способов определения неизвестных параметров модели условно подразделяются на методы моделирования процессов движения (развития) и экстраполяции (статистические методы).

К первой группе относятся методы, использующие дифференциальные уравнения с заданными начальными условиями. Задача прогнозирования сводится к решению дифференциальных уравнений для времени упреждения. Примером может служить математическое моделирование движения летательного аппарата на ЭВМ.

Ко второй группе относятся методы, основанные на обобщении статистических данных об изучаемом объекте (процессе). Результатом обобщения является некоторая аналитическая модель. Для определения неизвестных параметров модели наиболее часто используется метод максимального правдоподобия или его разновидность – метод наименьших квадратов, а также метод взвешенных наименьших квадратов. Задача прогнозирования сводится к вычислению ее значения для заданного момента времени (или при заданном значении какой-либо другой независимой переменной).

Логический анализ является завершающей стадией комплекса исследований, связанных с прогнозированием и в общем случае предусматривает: построение дерева целей и его анализ, выявление возможности и времени появления скачкообразных изменений в развитии процесса, оценку полученных результатов, изучение тенденции развития объекта исследования, обобщение результатов прогнозирования подобных объектов, устранение несоответствия принятой модели реальному объекту, построение морфологических моделей, которые в дальнейшем можно положить и в основу формализованных моделей прогнозирования.

Именно логический анализ результатов прогнозирования позволяет: устранить противоречия между функционированием элементов в системе прогнозирования и полученных результатов на различных этапах исследования, выявить соответствие и взаимосвязь между явлениями, исследованием которых занимаются науки, относящиеся к различным областям знаний.

Эвристическое прогнозирование. Предварительно проводится опрос и анализ результатов опроса, при котором интуитивно учитываем вес каждого эксперта в зависимости от субъективного представления о его компетенции в данном вопросе и благожелательности по отношению к нам и к нему.

Процесс эвристического прогнозирования характеристик технических устройств условно делится на три этапа:

– разработка прогноза развития естественных наук с целью составления обзора состояния известных разработок, которые можно завершить в фиксированные сроки,

– разработка прогноза возможных характеристик заданного технического устройства, которые могут быть достигнуты в указанные фиксированные сроки (после ознакомления с предыдущим прогнозом специалистами в области техники),

– обработка результатов, полученных различными экспертами независимо друг от друга.

Несомненным достоинством метода эвристического прогнозирования является возможность избежать грубых ошибок, особенно в области скачкообразных изменений прогнозируемой величины благодаря выбору в качестве экспертов высококвалифицированных специалистов данной области знаний. Ограничения метода связывают с его субъективизмом, значительной сложностью, трудоемкостью и стоимостью.

Математическое прогнозирование. Методы математического прогнозирования могут быть разделены на три группы: статистические (описательные), причинно-следственные и совмещенные.

Изучение любого процесса требует задать закон изменения входных переменных во времени. Выходные переменные могут быть описаны с помощью некоторой модели, значения коэффициентов которой определяются подбором. Различные наблюдения могут учитываться с различными весовыми множителями. Прогноз на основе статистической модели, включающей описание предыстории системы, состоит в расчете ее состояния для некоторого времени упреждения.

Для получения более точного прогноза необходимо построить модель, учитывающую причины изменений в системе объект – внешняя среда. Прогноз, полученный с помощью такой модели, позволяет более надежно предсказать будущее системы. Однако методы причинно-следственной группы требуют четко сформулированной математической модели поведения прогнозируемого объекта.

Выбор и обоснование модели является узловым вопросом математического прогнозирования и далеко не тривиальной задачей, в большинстве интересных для практики случаев требует специальных исследовательских проработок. Только в том случае, когда модель правильно описывает поведение изучаемого объекта, можно ожидать достаточно точные результаты прогнозирования.

Сложность оценки параметров модели зависит от степени искаженности информации об объекте прогнозирования. Точность прогноза будет тем выше, чем меньше искажений и чем больше имеющейся информации о прогнозируемом объекте. Математические методы идентификации моделей предполагают наличие некоторого критерия, использование которого позволит получить наилучшие в некотором смысле оценки неизвестных параметров модели.

При статистическом прогнозировании наиболее распространенным является критерий, дающий значения неизвестных параметров модели из условия минимума суммы квадратов отклонений прогнозируемой (расчетной) величины от ее наблюдаемых значений. Метод наименьших квадратов не всегда дает наилучшие результаты. Возможно использование критерия, дающего оценки неизвестных параметров модели из условия минимума «взвешенной» суммы квадратов указанных отклонений. Выбор критерия «наилучшей» оценки неизвестных параметров модели является вторым важным моментом при математическом прогнозировании и зависит от свойств объекта прогнозирования, требований к точности прогноза и т.п.

Статистическое прогнозирование использует только часть полного временного ряда. Связь между переменными определяется в любом случае. Такой прогноз, опираясь на хорошо отработанные методы отыскания подходящих моделей и методы уточнения прогнозов по новым наблюдениям, позволяет:

– делать предположения о возможности и моментах появления экстремумов в рассматриваемой временной зависимости переменных системы, а также о значениях переменных в экстремальных точках,

– получить хорошие результаты при уточнении принятых решений, распространяющихся на относительно короткие промежутки времени (обычно эти промежутки в десять раз больше интервалов между уточнениями предсказаний).

Между результатами прогноза и основными показателями функционирования системы возможна причинная связь. Поэтому существует опасность бессмысленного использования множественной регрессии в поисках «хорошего» коэффициента корреляции между прогнозируемыми (выходными) переменными и различными входными переменными. Необходимо обратиться к прогнозам на основе анализа причинно-следственных связей, которые позволяют предсказать моменты появления экстремумов и значения переменных в экстремальных точках.

Успешное решение задачи прогнозирования при применении математических методов определяется правильностью выбора математической модели (адекватностью ее прогнозируемому процессу) и точностью оценки ее неизвестных параметров. Наилучшие результаты получаются при использовании совмещенных статистических и причинно-следственных методов прогнозирования.

Комбинированное прогнозирование. Эвристическим и математическим методам прогнозирования присущи соответствующие ограничения, которые, в известной степени, сужаются при использовании комбинированной методики прогнозирования[197].

В наиболее общем случае такая комбинация имеет следующую последовательность. Из исследования модели процесса развития (движения) явления определяются общие закономерности (вид уравнений, описывающих изменения параметра, возможные области перерывов постепенности), при этом в них могут быть коэффициенты или даже функции, которые не удается определить на основании анализа закономерностей изучаемого процесса.

Эти коэффициенты (функции) определяют статистическими методами, исходя из статистических данных о течении процесса на участке наблюдения. Полученные таким образом зависимости позволяют вычислить математический прогноз. Независимо от него осуществляется эвристический прогноз, и затем результаты математического и эвристического прогнозирования сравниваются. В случае их непротиворечивости после совместной обработки результатов задачу прогнозирования можно считать решенной. В случае противоречивости приходится прибегать к методу логического анализа, с помощью которого и принимать окончательное решение. В каждом конкретном случае последовательность этих операций может быть разной.

5. Эвристическое прогнозирование.

Метод прогнозирования. Разработка методов прогнозирования на всех этапах непосредственно связана с творческой (эвристической) деятельностью. Даже желание использования чисто количественных методов потребует изучения имеющегося по данному вопросу фактического материала, анализ которого позволит перейти к следующему этапу – абстрактному мышлению. Необходимо разобраться в основных факторах, которые следует учитывать при проведении количественных оценок, разработать гипотезы о возможных механизмах взаимосвязи между основными параметрами процесса и сформулировать его аксиоматику, которая и предопределяет содержание всех дальнейших результатов. Именно здесь реализуется главное преимущество мозга по сравнению с вычислительными машинами, отмеченное Н. Винером[198]: способность оперировать с нечетко очерченными понятиями.

Эвристическая деятельность на начальном этапе исследования является решающим фактором, определяющим качество прогноза, который получается в дальнейшем. Пока невозможно выйти за рамки понятия начальных этапов прогнозирования как искусства. «Умственная деятельность здесь покидает область строгого знания, логики и математики и превращается в искусство в более широком смысле этого слова, т.е. в умение интуитивно выбирать из бесчисленного множества предметов и обстоятельств важнейшие и решающие. Большая или меньшая часть этой интуиции состоит в полусознательном сравнении всех величин и обстоятельств, с помощью которого быстро устраняется все маловажное и несущественное, а более нужное и главное распознается скорее, нежели путем строго логических умозаключений» (К. Клаузевиц,1936)[199].

Основой аксиоматики при ее формировании служит имеющийся экспериментальный материал как результат познания изучаемого объекта. Количество экспериментальных данных и полнота учета в них основных параметров процесса, которые могут быть в настоящее время измерены, существенно влияют на аксиоматику. Появление новых экспериментальных данных приводит к необходимости пересмотра принятой аксиоматики. Именно поэтому для проведения экспертных опросов привлекают людей с большим опытом. Такой опыт достаточно ограничен, и необходимо использовать дополнительно весь имеющийся содержательный материал, относящийся к проблеме исследования.

С ростом возможностей вычислительной техники в области решения задач прогнозирования на уровне вспомогательных операций роль эвристической деятельности может быть снижена. Это относится, например, к решению задач информационно-поискового характера, проведения предварительного факторного анализа путем обработки собранных экспериментальных данных, установления основных корреляционных связей между определяющими параметрами процесса. Следовательно, человек сможет больше времени и сил тратить на непосредственно творческую сторону исследования – выработку взглядов относительно первопричин, которые приводят к обобщению полученных корреляций до уровня открытия законов природы.

Эвристическая деятельность человека, которая лежит в основе прогнозирования, смещается в область абстрактного мышления для формирования приемлемых гипотез Опровержение или подтверждение природой (или системой экспериментальных данных) выдвинутых гипотез и является завершающим элементом теории познания. В случае подтверждения гипотез опытом можно переходить к практике – к управлению процессом или к учету и использованию выявленных свойств явления.

В большинстве случаев качественная информация воспринимается человеком наряду с количественными характеристиками процессов. В настоящее время отсутствуют сопоставимые с возможностями человека математические методы построения образов при существенном количестве чисто качественной информации. Необходим этап анализа экспертами результатов, полученных при количественном анализе, чтобы выявить возможные причины появления нескольких генеральных совокупностей при обработке экспериментальных данных.

Чисто эвристическое прогнозирование неотъемлемо связано с основными этапами построения модельных представлений эксперта. Обучение эксперта происходит в течение всей его практической деятельности. Он проводит для себя факторный анализ, выявляя главное в процессе, составляет представление о взаимосвязи между основными параметрами, как это было раньше, на основе чего и получает возможность сделать предположения о возможном развитии системы в будущем.

Аспекты восприятия и оценки ситуаций. Главный вопрос, который возникает при прогнозировании, и ответ на него посредством эвристических методов – это правильная оценка нового (новых знаний). Как известно, при восприятии нового проявляется ряд качеств, которые отрицательно сказываются на получаемых оценках[200].

Во-первых, это – профессиональная ограниченность. Большие трудности возникают при оценке перспективности новых направлений, развивающихся на стыке различных областей знаний. Эти трудности являются следствием сложившейся к настоящему времени методологии научных исследований, которые ведутся в двух основных направлениях.

Первое направление связано с упрощением, сведением сложного к более простому, доступному для анализа или решения (редукция знаний). Суть другого направления, состоит в рассмотрении целостных систем, уровень организации которых соответствует характеру изучаемых функций (интеграция знаний). Формулировка позиций этого направления сделана Платоном, который считал, что «целое есть нечто большее, чем простая сумма его частей». В связи с этим понятно утверждение о потребности в специалистах по системе в целом, которые и должны до конца представлять себе, почему же целое нечто большее, чем простая сумма его частей.

Естественным следствием существования этих направлений является наличие специалистов узкого и широкого профиля. Специалисты в конкретных областях знаний более склонны абсолютизировать некоторые конструктивные решения, упускать из вида возможности появления новых конкурирующих направлений[201].

Во-вторых, невосприимчивость из-за различной направленности мышления, называемая также психологической инерцией. Как правило, исследователь отдает предпочтение тем фактам, которые подтверждают его мнение, нежели тем, которые противоречат его убеждениям. Во многих случаях даже при высокой квалификации экспертов возможно невосприятие ими перспективной идеи.

Считается, что человек, погруженный в определенный круг мыслей, часто страдает своеобразной «слепотой» и «глухотой» к тому, что находится за пределами его интересов, не приемлет лежащего вне его сферы профессионализма. «Великая научная идея редко внедряется путем постепенного убеждения и обращения своих противников. В действительности дело происходит так, что оппоненты постепенно вымирают, а растущее поколение с самого начала осваивается с новой идеей» (М. Планк)[202].

В-третьих, концентрация внимания преподавателей на известных явлениях. Эту психологическую особенность восприятия нового отметил Луи де Бройль[203], который считал, что преподаватель концентрирует свое внимание на известных явлениях, так как в ходе обучения вынужден стремиться к канонизации знаний, в то время как исследователь более склонен интересоваться неизвестными сторонами процессов и явлений. В связи с этим преподавателям чаще свойственна привычка к консерватизму мышления по сравнению с исследователями.

В-четвертых, трудность восприятия отрицательных выводов. Опыт показывает, что суждения, которые утверждают или обосновывают какой-то отрицательный вывод, воспринимаются особенно трудно. Невозможность создать вечный двигатель, решить задачу о квадратуре круга и др. потребовали для своего обоснования больших интеллектуальных усилий человечества.

В-пятых, склонность к преувеличению плохого.

В-шестых, нежелание и боязнь нести ответственность за дефекты своей науки. Клаузевиц считал[204], что «первая причина, которая вызывает постоянную склонность к остановке и через то становится тормозящим началом, – это природная боязливость и нерешительность человеческого духа, своего рода сила тяжести в моральном мире, которая, впрочем, вызывается не силами притяжения, а силами отталкивания, именно – боязнью опасности и ответственности».

В-седьмых, зависимость восприятия от хода исследования. На интересную особенность восприятия нового, связанную с зависимостью восприятия от хода исследования, обратил внимание Гете[205]: «Каждый путь, по которому мы приходим к открытию, влияет на взгляды и теории. Мы едва ли задумываемся, что привело нас к этому явлению, над его началом и причиной; на этом мы останавливаемся, вместо того, чтобы подойти с другой стороны и проверить наши первоначальные догадки и получить правильное представление о целом. Что бы мы сказали об архитекторе, который пошел бы во дворец через боковую дверь и, описывая и изображая это здание, сослался бы на эту второстепенную сторону? А в науке это происходит ежедневно».

В-восьмых, влияние направлений общественной мысли. Общественный резонанс не пропорционален академическому значению научных работ, вызывающих этот резонанс; и не всегда научные открытия поддерживаются прогрессивными элементами общества, а отвергаются ретроградами и реакционерами (бывали и обратные случаи).

На основе анализа восприятия нового были сформулированы условия, необходимые для своевременной оценки научного открытия:

– подготовленность научной мысли к восприятию новой идеи, накопление значительного числа фактов, связанных с темой открытия;

– большая степень адекватности результатов, полученных в ходе нового исследования, тем задачам, которые возникли в ряде предыдущих работ;

– наличие достаточных средств информации для широкого ознакомления научной общественности с результатами новых исследований.

Известно большое количество открытий, намного опередивших свое время и поэтому не воспринятых современниками.

Приведенные особенности восприятия нового можно объяснить частично с позиций основных свойств образов мышления и внимания, которые характерны для различных людей.

Динамические свойства образов мышления, связанные с принятием решения, подразделяют на: остаточные, инертные, опережающие образы.

Остаточный образ – перенос прошлой ситуации в неизменном виде в новую ситуацию, характеризуется статичностью мышления, пониженной восприимчивостью.

Инертный образ – оценка текущей ситуации мыслится как окончательный результат, связан с высокой статичностью мышления, самоуспокоенностью, снижением способности к предвидению.

Опережающий образ – возможные будущие изменения воспринимаются как реально существующие, которые вытесняют действительность. Приводит к снижению продуктивности мышления и недостаточной восприимчивости.

С другой стороны, основные свойства внимания характеризуют его устойчивость, восприимчивость, сосредоточенность и интенсивность. Они определяются индивидуальными особенностями внимания, которые, в частности, зависят от теоретических знаний и опыта, эстетических и научных взглядов, характера рассматриваемого процесса, моды. Подбор экспертов, обладающих этими свойствами, представляет чрезвычайно сложную проблему[206].

При оценке ситуаций определенную роль играют психические особенности человека. Интересны следующие результаты, полученные при использовании шахмат, как удобной модели для изучения творческих процессов.

Возможна следующая классификация стилей игры[207]:

– классический стиль – выбор плана производится не вслепую, а разумно, то есть сообразно с принципами «здравого смысла»;

– стиль «автомата», делающего ходы всегда по готовому шаблону из запаса памяти;

– «прочный» стиль укрепления позиции и выжидания ошибки противника;

– комбинационный стиль.

Ж. Адамар впервые обосновал положение, что шахматный стиль – отражение свойств характера человека, и по игре можно определить характер и темперамент шахматиста. Это положение достаточно общее, и его можно подтвердить исследованием результатов управления сложными системами людьми с различными психологическими характеристиками.

Реализация управления сложными системами всегда связана с необходимостью прогнозирования характеристик процесса. На их основе принимаются решения об управляющих воздействиях, обеспечивающих достижение поставленных целей. Качество прогнозирования закономерностей функционирования системы определяет результирующие характеристики управляемого процесса. Характер экспертов, производящих прогнозирование и на этой основе реализующих управление процессом, в той же мере оказывает влияние на общие его результаты. Отбор экспертов должен проводиться в соответствии с особенностями решаемой задачи.

Использование метода. Эвристическое прогнозирование основано на усредненной оценке мнений группы экспертов. Чтобы получить достаточно хорошие для практического использования результаты прогнозирования, необходимо организовать проведение опросов, подбор экспертов и обработку полученных результатов так, чтобы по возможности исключить принципиальные недостатки, связанные с эвристическим прогнозированием.

Основным методом организации экспертных опросов является метод Дельфи [см. лек-
цию 23] и его модификации[208], использование которого предполагает определение «информированного интуитивного суждения». Исходят из следующих основных правил: опрос проводится в несколько туров, ответы обязательно даются в количественной форме, после каждого тура проводится статистическая обработка результатов опроса и все опрашиваемые эксперты знакомятся с ответами других участников опроса, от экспертов требуют обоснования их мнений, эти обоснования доводятся до других участников опроса, эксперты дают ответы независимо друг от друга.

Главным условием является подбор экспертов. Качество результатов существенно зависит от их компетентности. Правильный подбор экспертов связан с определением степени их квалификации, что является достаточно сложной задачей. Полностью объективных методов оценки степени компетентности при проведении опросов нет. Используют метод самооценки специалистами своей компетентности и компетентности других экспертов. При опросе эксперту предлагают назвать несколько человек, которых он считает компетентными в данном вопросе.

Следующее условие связано с необходимостью создания обстановки для плодотворной работы экспертов. Продуктивность резко возрастает, если эксперт имеет полный доступ к информации, относящейся к рассматриваемому вопросу.

Наиболее эффективным способом усиления взаимодействия между специалистами является проведение «мозговых атак» в различных вариантах [см. лекцию 23]. Прямая «мозговая атака» основана на гипотезе, что среди большого количества идей имеется, по крайней мере, несколько хороших. Используются также другие методы. Например, «стимулирование наблюдения»[209], в ходе которого рассматривается некоторая принципиально абстрактная ситуация (хотя бы жизнь на другой планете). Цель таких исследований – привести эксперта в «спортивную форму».

При использовании метода Дельфи[210] [см. лекцию 23] полностью устраняется непосредственное общение специалистов, которое заменяется программой последовательных индивидуальных опросов, проводимых, как правило, с помощью анкет. Это позволяет избежать чрезмерного влияния ряда психологических факторов, возникающих при проведении коллективных дискуссий.

Часто трудно подобрать достаточно большое количество экспертов. Это приводит к тому, что при небольшом времени прогнозирования (3–10 лет), как правило, не требуется проводить повторные опросы. Получаемые в результате прогноза оценки оказываются достаточно стабильными.

Успех экспертного опроса в значительной мере зависит от четкости постановки вопросов, исключающих неоднозначность толкования. Это, в свою очередь, требует определенной формы анкеты, которая должна быть лаконичной, на оформление результатов эксперт должен тратить минимум времени.

Вообще говоря, по результатам опроса экспертов можно проконтролировать их компетентность и темперамент. При этом признаками могут служить следующие величины: коэффициент вариации vj = ?j/Mj, где Mj – точечный прогноз данного эксперта (среднее значение); ?j – среднеквадратическое отклонение; величина Mj/M – 1, где M – точечный прогноз всей группы экспертов. По приведенным признакам классификация экспертов приведена в таблице [табл. 17].

Необходимость классификации экспертов напрямую связана с правильной оценкой результатов экспертизы. При проведении экспертных опросов автор нового направления или просто эксперт, лучше представляющий пути развития некоторой отрасли науки и техники, может оказаться за пределами генеральной совокупности ответов, которые дают остальные эксперты. К крайним точкам зрения относятся особенно внимательно, изучаются доводы в защиту такой точки зрения, анализируются основные факторы, которые могли затруднить высказывание подобной точки зрения остальными экспертами.

Таблица 17

Признаки классификации экспертов

6. Статистическое прогнозирование.

Статистическое прогнозирование – это множество методов многократного уточнения значений некоторого параметра модели, который используется в качестве прогнозируемой характеристики системы. Методики реализуются двумя подходами. В первом случае оценка основана только на имеющихся данных и потому проводится лишь один раз. Во втором случае оценки пересматриваются по мере поступления новой информации, что позволяет получать новые значения выходной переменной системы и корректировать выбор варианта решения. Пересмотр и уточнение оценок (прогнозов) могут проводиться либо через одинаковые интервалы времени (например, через неделю или месяц), либо через разные интервалы времени (например, в аналоговых системах, применяемых для контроля над пожароопасными объектами, используются специальные методы последовательной проверки наличия или отсутствия опасности).

Виды временных рядов. Можно выделить два вида прогнозируемых характеристик системы, зависящих от времени: переменные состояния и переменные интенсивности[211]. Переменная состояния определяется периодически, и ее значение в течение небольшого интервала времени не зависит от времени, прошедшего с момента начала наблюдения. Переменная интенсивности также определяется периодически, но ее значение пропорционально времени, прошедшему с момента предыдущего наблюдения. Такие характеристики системы, как температура, скорость, число подписчиков на журнал или цена, являются примерами переменных состояния. В качестве примера переменной интенсивности можно привести количество выпавших осадков, количество проданных экземпляров или спрос. Если переменная состояния характеризует количество, то временная интенсивности – скорость его изменения.

Прогнозы обычно осуществляются для нескольких последовательных интервалов времени в пределах некоторого времени упреждения, по истечении которого становятся важными результаты реализации принятых решений. Можно выделить следующие особенности прогнозирования переменных состояния и интенсивности:

– если измерения характеристик системы проводятся через разные интервалы времени, то величину интервала необходимо учитывать при оценке переменных интенсивности, при оценке переменных состояния эта величина не имеет значения;

– правильный прогноз переменной состояния должен определять ее значение в конце времени упреждения; прогноз переменной интенсивности должен представлять собой сумму прогнозов на протяжении времени упреждения;

– для переменной состояния функция распределения во времени вероятностей ошибок прогноза должна соответствовать функции распределения вероятностей ошибок в исходных данных; для переменной интенсивности закон распределения вероятностей ошибок прогноза во времени стремится к нормальному при любом законе распределения вероятностей ошибок в исходных данных, поскольку эти ошибки представляют собой сумму ошибок прогноза в отдельные интервалы времени.

Интервалы пересмотра и уточнения прогноза. С целью уточнения ранее сделанных прогнозов о выходных переменных проводят многократные измерения входных переменных системы. Величина промежутков времени между замерами зависит от длительности времени упреждения и наибольшей частоты циклических изменений в системе, которые должна отражать модель. Однако они должны быть достаточно велики, чтобы проявлялись ожидаемые изменения в поведении системы. В течение времени упреждения прогноз чаще всего проверяется один-два раза, но иногда возникает необходимость увеличить количество проверок. Это зависит от условий решаемой задачи.

Когда имеют место какие-то периодические процессы, как, например, при годовых изменениях температуры теплоносителя в сети отопления, частота наблюдений должна быть по крайней мере вдвое больше частоты изучаемого процесса. Очевидно, что наблюдения с интервалами один раз в полгода не будут способствовать правильной организации работы котельной зимой в отличие от ее работы весной. Наблюдения с интервалами в сутки не дадут возможности обнаружить различие в интенсивностях работы первой и второй смен.

Если случайная ошибка при определении входных переменных велика по сравнению с измеряемой величиной, то с целью усреднения случайной ошибки интервал уточнения прогноза для переменной интенсивности целесообразно увеличить. Однако для переменной состояния его лучше уменьшить, что позволяет использовать для выделения полезного сигнала методы фильтрации[212].

Исходные данные. Исходные данные обычно представляют собой результаты выборочных наблюдений либо переменной интенсивности, такой, как расход энергии, либо переменной состояния, такой, как ее цена. Решения, которые должны приниматься в данный момент времени, скажутся в дальнейшем по прошествии некоторого промежутка времени – времени упреждения. Величина этого промежутка времени может быть прогнозируемой переменной.

Исключение выбросов. Результаты наблюдений регистрируются с большим количеством ошибок, которые возникают как при наблюдениях, так и при регистрации данных. Кроме того, изучаемый процесс может иметь стохастическую природу. Результаты наблюдений могут содержать и аномальные эффекты, например, необычайно высокий расход энергии во время холодов или чрезмерно высокую температуру в помещении в случае перегрева термостата. Поэтому не каждую совокупность зарегистрированных по мере поступления реальных данных следует считать подходящим временным рядом, на основании которого можно составлять прогноз. Перед тем как подобрать коэффициенты модели по исходным данным, из последних должны быть исключены выбросы, т.е. результаты наблюдений, которые не характеризуют прогнозируемый процесс.

Простой и надежный способ такого исключения выбросов состоит в следующем. Наибольший и наименьший результаты наблюдений могут представлять собой выбросы. Поэтому эти два результата временно исключаются из имеющейся выборки данных. Интервал между крайними оставшимися результатами наблюдений позволяет быстро оценить область нормального изменения исходных данных. Величина интервала между максимальным и следующим по величине (или минимальным и ближайшим к нему) значениями входной переменной может служить индикатором того, что экстремальные результаты являются представительными.

Для отрезков временного ряда, содержащих от 20 до 100 наблюдений и превышающих сорок процентов основного ряда, целесообразно проверять исходные данные более тщательно. Очевидно, этот простой тест не позволит исключить ни двух выбросов одного знака, если оба они достаточно велики, ни отклонений в данных, имеющих чисто гармоническую природу при значимом негармоническом периоде. Если разброс данных превышает, например, 4?, то требуется более тщательный отбор входных переменных, с тем чтобы после подбора коэффициентов получить статистическую модель, правильно описывающую исследуемый процесс.

Преобразование исходных данных. Различные виды данных часто подчиняются экспоненциальным зависимостям. В таких случаях при построении моделей процесса удобно пользоваться логарифмическим масштабом. Другим видом преобразований является разбиение исходного ряда данных на составные ряды, каждый из которых легко описать. Например, хотя решения о величине запаса топлива принимаются на полный календарный год, общий расход топлива на отопление трудно прогнозировать с помощью одной общей модели. Удобнее прогнозировать, используя отдельные ряда данных для различных периодов отопительного сезона.

Помехи, остатки и ошибки. Для описания стохастических элементов временных рядов и их прогноза используются три различных понятия – помехи, остатки и ошибки. Понятие помехи связано с собственной изменчивостью процесса и неопределенностью, вносимой при наблюдении за ним. Следовательно, помеха является составной частью используемых данных. Под остатками понимается разность между результатами текущих наблюдений и значениями, вычисленными с помощью прогнозирующей их модели. Остатки связаны с прошлыми данными и моделью, которая использовалась для их оценок. Ошибки прогноза представляют собой разницу между прогнозом, сделанным в настоящее время, и тем, что будет наблюдаться позднее в момент времени, для которого составлен прогноз.

Условие стационарности процесса. Любой процесс, представленный рядом результатов наблюдений, можно, по крайней мере, схематически описать набором разностных уравнений (когда процесс дискретен) или дифференциальных уравнений (когда он непрерывен). Если в этих уравнениях коэффициенты не зависят от времени, процесс называется стационарным, если же зависят, то нестационарным. Эта зависимость может носить вероятностный или регулярный характер. Очевидно, что регулярное изменение коэффициентов во времени может быть описано дополнительными уравнениями.

Для достаточно длительных интервалов времени большинство прогнозируемых рядов является нестационарным. Они могут считаться квазистационарными, если прогноз составляется для какого-то одного момента времени.

Модели. Пусть в момент времени ?o задана последовательность результатов наблюдений X? для некоторого множества моментов времени ? ? ?o. Прогнозирующая модель задает множество выходных переменных 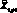, которые могут быть выражены в векторной форме (время ? > 0).

Выражение для прогнозирующей модели может быть записано, как 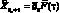, где вектор представляет собой коэффициенты модели, полученные по результатам наблюдений до момента ?o включительно, а матрица 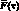– набор аппроксимирующих функций. Строки матрицы соответствуют элементам модели, а столбцы – моментам времени. В большинстве практических приложений 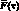определяет время относительно момента самого последнего наблюдения, а значения коэффициентов зависит от выбора начала отсчета времени.

Полиномиальное представление временных рядов. Весьма общий класс составляют модели, которые могут быть представлены с помощью вещественных полиномов Fi:

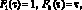
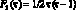и т.д.

Применение различных методов прогнозирования позволяет получить различные модели, например, за счет использования разностей или сумм отдельных функций[213] Fi. Поскольку решение линейного дифференциального уравнения может быть представлено в виде вещественного полинома, то различные математические описания моделей означают для нас лишь возможность выбора удобной формы анализа, а не фактическое различие в математических свойствах таких моделей.

Довольно часто для анализа локальных изменений в наблюдаемых данных достаточно использовать полином первой степени (прямую линию). Константа, как полином нулевой степени, является частным случаем полинома первой степени, в котором коэффициент при линейном члене равен нулю. Подгонка прямой линии для конкретного ряда прогнозируемых данных производится путем варьирования величины второго коэффициента, отражающего тенденцию изменения временного ряда за длительный период времени (вековой тренд). Если величина этого коэффициента мала, то его можно исключить из модели.

Величины коэффициентов, которые могут быть исключены из модели, в соответствии со статистическим критерием настолько малы, что их исключение не оказывает никакого влияния на краткосрочный прогноз. Затраты на осуществление статистического теста могут быть больше, чем затраты на использование такой малой величины в прогнозе, даже в случае, когда в ее использовании нет никакой необходимости. Если время упреждения более чем
в 10 раз превышает величину интервала времени между уточнениями прогноза, исключение трендов из модели становится более важным.

Математические методы позволяют представить прогнозирующую модель в виде полинома любого порядка[214]. Если решаемая задача не требует использования полиномов более высокого порядка (как, например, при отслеживании траектории баллистической ракеты), то их применение для описания прогнозируемых рядов оказывается излишним.

Сезонные модели. Уровень воды в море изменяется дважды в сутки за счет приливов. Температура в области высоких широт ежегодно меняется от высокой до низкой и обратно. Потребление электроэнергии ежедневно изменяется по более сложным зависимостям (исключая большие праздники и годовой цикл). Расход топлива на отопление может меняться по циклам, повторяющимся каждый год. Учет подобных периодических (сезонных) колебаний в общей модели может повысить эффективность прогноза и позволит предсказывать ожидаемые высокие и низкие значения прогнозируемых переменных.

Не все ряды, имеющие высокие и низкие значения переменных, обязательно цикличны в указанном смысле. Деловые или экономические «циклы» не повторяются с достаточной воспроизводимостью, позволяющей на практике, исходя из анализа прошлого, делать выводы о каких-то будущих подъемах и спадах.

Для описания сезонных моделей существуют два совершенно разных подхода, каждый из которых имеет множество вариантов.

Пусть N – число результатов наблюдений за какой-то период времени. Например, N = 12 для годового цикла или N = 7 для недельного цикла. Можно записать либо N поправочных членов (положительных и отрицательных), которые затем суммируются с результатами прогноза, либо N коэффициентов, каждый из которых больше или меньше единицы, которые умножаются на него. Значения поправочных коэффициентов можно определить по результатам наблюдений в соответствующие моменты времени в прошлых циклах. Например, в некоторых простейших методах такие значения, скажем, для сентября месяца, определяются на основе данных для этого же месяца в прошлые годы. В более сложных методах[215] осуществляются усреднение и учет результатов наблюдений, которые предшествовали данному наблюдению.

При анализе потребления топлива в системе теплоснабжения сезонные коэффициенты используются в качестве кумулятивных характеристик, которые представляют процентное выражение сделанного к настоящему времени по отношению к тому, что должно быть сделано в течение полного периода.

В любом из названных подходов весь ряд поправочных членов или коэффициентов может быть назван сезонным «сечением». Показано, что на практике существует небольшое семейство сечений. Сечения, бесспорно, играют важную роль в методике прогнозирования, так как их сущность легко объяснить, а эффективность их использования легко оценить на практике. Прогнозы для отдельных временных рядов могут быть получены путем выбора наиболее подходящего представления этого семейства.

Существенным ограничением применения сечений является связанная с ними нестабильность прогноза. Если случайная величина x имеет дисперсию ?2, то дисперсия обратной величины 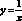– порядка ?4. В большинстве методов, использующих сезонные или циклические сечения, на некотором этапе вычислений проводится деление на случайную переменную (или ее оценку, имеющую отличную от нуля дисперсию). Если знаменатель имеет тот же порядок величины, что и помеха, то относительно малые колебания исходных данных могут привести к большим изменениям прогноза. К сожалению, подобная нестабильность обычно проявляется как раз тогда, когда принимаемые решения могут иметь самые серьезные последствия (т.е. перед началом следующего цикла).

Уменьшить подобную нестабильность можно, используя дисперсию помехи как функцию среднего по всем наблюдениям за цикл и не зависящую от сезонных изменений[216]. При этом чувствительность метода к колебаниям данных в точках высших и низших значений прогнозируемых переменных соответственно повышается и понижается.

Другой подход заключается в представлении циклических изменений прогнозируемой переменной рядами Фурье:

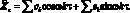
Здесь ck и sk – коэффициенты, полученные по исходным данным с помощью соответствующей регрессии, ? = 2?/f – основная частота, f – число наблюдений в одном сезонном цикле, ? – время, за которое должен быть вычислен прогноз, k = 1, 2, ..., N. Суммирование ведется по всем частотам вплоть до частоты Найквиста (наивысшей частоты гармонического разложения дискретного ряда, которая определяется половиной интервала между наблюдениями).

Достоинство такой модели[217] состоит в том, что она обеспечивает стабильность прогноза даже в точках цикла с наименьшими значениями прогнозируемой переменной, так как коэффициенты вычисляются путем усреднения всего набора имеющихся данных, а не только результатов наблюдений в пределах одного цикла. Хотя на практике подобная модель оказывается сложной для пользователя.

Если для составления прогноза используются только первые члены разложения Фурье, то сезонное сечение представляет собой простую синусоиду с некоторой амплитудой и фазой, зависящими от коэффициентов c1 и s1. При увеличении числа членов разложения форма сечения может измениться. В соответствии с теоремой Фурье, если в дискретных рядах величина переменной повторяется через каждые f наблюдений, то такие ряды могут быть представлены точно f членами гармонического разложения. Амплитуда j-й гармоники, включенной в модель, равна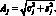

Квадрат амплитуды иногда называют мощностью данной гармоники. Пусть ?2 – дисперсия остаточных разностей между исходными данными и результатами расчетов по модели, включающей гармоники вплоть до j-й. Модель будет соответствовать предыстории, охватывающей от 3 до 6 предыдущих циклов, если выполняется соотношение 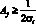. Проверка на соответствие предыстории обычно проводится по критерию наименьших квадратов. Отметим, что при вычислении ?2 необходимо учесть потерю степеней свободы некоторым числом переменных в модели. Это означает, что минимальную дисперсию можно достичь, используя модель с числом переменных меньше f. Однако такая модель будет неверной, если мощность включенной в нее высшей гармоники не будет достаточно большой по сравнению с остаточной дисперсией.

Анализ временных рядов. Допустим, что ряды X? приведены к рядам с нулевым средним 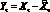, причем в модели для переменной 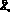предусматривается согласование полиномиальных трендов и циклических изменений. Автоковариация 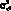представляет собой ожидаемое значение произведения 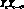, где ?* – время задержки. Если модель 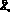отражает все периодические колебания в данных, то автоковариация в основном равна нулю для всех значений времени задержки. Большие значения автоковариации (положительные или отрицательные) указывают на то, что в рядах имеется информация, которая может быть внесена в модель. Математические методы отыскания адекватной модели описания временных рядов составляют специальную область статистики – спектральный анализ[218].

Вероятностные модели. При представлении совокупности результатов наблюдений в виде временных рядов фактически используется предположение о том, что наблюдаемые величины принадлежат некоторому распределению, параметры которого и их изменение во времени можно оценить. К параметрам относят среднее значение и дисперсию, хотя иногда используется и более полное описание. По этим параметрам можно построить одну из моделей вероятностного представления процесса.

Другим вероятностным представлением является модель в виде частотного распределения с параметрами pj для относительной частоты наблюдений, попадающих в j-й интервал. Если в течение принятого времени упреждения не ожидается изменения распределения, то решение принимается на основании имеющегося эмпирического частотного распределения.

Система сглаживающих весовых множителей. Практически во всех применяемых в настоящее время методах прогнозирования реализуется следующая методология. Сначала определяются коэффициенты моделей (например, 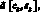или pj) путем ее подгонки к некоторым данным предыстории. Затем они проверяются и уточняются по мере поступления новых данных. Выбор коэффициентов осуществляется из условия минимизации суммы квадратов остаточных разностей между данными и результатами расчета по модели. При этом учитываются различные весовые множители, приписываемые остаткам в различные моменты времени. Например, коэффициенты a могут выбираться на основе минимизации величины 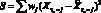, где суммирование проводится по всем j вплоть до самого последнего наблюдения в момент времени ?o. При оценке тех или иных достоинств различных систем весовых множителей wj необходимо учитывать не только достигаемую при их использовании точность прогноза, но и степень сложности соответствующих вычислений.

Одинаковые весовые множители. Простейший ряд весовых множителей wj = 1 для всех j из интервала 0 ? j ? ?o придает одинаковую значимость всем членам временного ряда. Первоначальные значения коэффициентов в любом случае получаются путем простой подгонки модели по методу наименьших квадратов, при котором все члены ряда имеют одинаковую значимость. В дальнейшем коэффициенты модели будут уточняться и возможно применение некоторой другой системы весовых множителей.

Скользящее среднее представляет собой оценку по методу наименьших квадратов единственной константы для представления исходных данных с одинаковыми весовыми множителями. Этому случаю соответствует простая функция F(?) = 1 для всех ?. При этом весовые множители wj = 1 для N последних наблюдений в интервале 0 ? j ? N – 1 и wk = 0 для k ? N.

Некоторые коэффициенты модели могут определяться с помощью полиномов более высокого порядка путем подгонки модели к результатам N самых последних наблюдений в каждый момент поступления новых данных. В самом общем случае значения коэффициентов в любой заданный момент времени зависят от: предыдущих значений коэффициентов, ошибки в прогнозе при использовании самого последнего наблюдения, вида используемого полинома, числа N результатов наблюдений.

Оптимальные весовые множители. Для стационарных временных рядов существует система весовых множителей, позволяющая обеспечить минимальную ошибку прогноза. Эти множители определяются видом автоковариационной функции. Предложен также метод вычисления таких оптимальных весовых функций для постоянного уровня, тренда и сезонных коэффициентов[219]. В каждом из этих случаев весовые множители экспоненциально уменьшаются по закону ?j, а различные значения ?, получаемые для уровня, тренда и сезонных коэффициентов, определяются путем систематического исследования точности прогнозов, получаемых при различных комбинациях весовых функций.

Для достаточно широкого класса моделей предложен метод[220], основанный на сочетании вычисления автоковариационной функции с систематическим исследованием области, в которой при определенном периоде и временной задержке должны находиться оптимальные весовые множители. Данный метод эффективен при большом объеме обрабатываемых данных или если известны основные закономерности изучаемого процесса. Впервые результаты этой работы были с большим успехом применены в химической промышленности при создании системы управления технологическим процессом, работающей в реальном масштабе времени.

Весовые множители с экспоненциальным затуханием. Во многих случаях целесообразно использовать последовательность wj = ?j, ? < 1, придающую более высокий вес более поздней информации и позволяющую относительно просто оценивать значения коэффициентов даже достаточно сложных моделей. Для описания сезонных циклов используются полиномы в сочетании с преобразованиями Фурье. Подобное представление можно рассматривать как сложные полиномы.

Указанные достоинства экспоненциального сглаживания[221], сделавшие его достаточно популярным, особенно важны в тех случаях, когда уточнение прогноза необходимо проводить многократно, а стоимость вычислений может оказаться довольно большой по сравнению с затратами на составление менее точного прогноза.

Для модели экспоненциально взвешенного скользящего среднего предложены способы[222], с помощью которых скорость затухания ? может быть увеличена в те периоды времени, когда средняя ошибка прогноза близка к нулю. Благодаря правильности модели и ее коэффициентов, скорость затухания ? может быть уменьшена в те периоды времени, когда средняя ошибка прогноза существенно отличается от нуля и существует опасность того, что модель может забыть старую информацию. В этом случае требуется уточнение прогноза.

Уточнение прогноза производится по принципу обратной связи. Новые прогнозы корректируются на основе учета ошибок в предшествующих прогнозах. Если в процессе составления прогноза при выборе весовых множителей также используется обратная связь, то любой анализ становится фактически невозможным, в том числе и строгий анализ областей устойчивости данной системы. Для анализа эффективности какого-либо метода мало привести примеры, подтверждающие его полезность. Необходимо также выявить области (если они существуют), в которых его применение невозможно или неэффективно.

Многие методы позволяют отыскать наилучшее значение скорости затухания весовых множителей путем многократного анализа имеющегося ряда данных. При этом в качестве критерия используется достигаемая точность прогноза (минимальная дисперсия ошибки). Однако такой подход содержит и недостатки.

Во-первых, если в средней ошибке есть значимые разности (они должны быть равны нулю), то более вероятно, что эти разности больше зависят от способа выбора начальных значений коэффициентов модели, чем от различий в скорости затухания весовых множителей или постоянной сглаживания.

Во-вторых, еще более важный источник возможной ошибки можно проиллюстрировать с помощью следующего примера. Будем рассматривать очень длинный ряд чисел, как некоторый коррелированный процесс. Стационарность и однородность ряда гарантирована самим способом его получения. Разделим его на короткие отрезки, содержащие достаточно данных для отыскания наилучшего значения скорости затухания весовых множителей. Проанализируем результаты, получаемые для каждого из этих отрезков. Окажется, что существует широкое распределение соответствующих значений скорости затухания. Определить скорость затухания для данного отрезка можно только после того, как он стал историей. Величина скорости на следующем отрезке, которая может быть другой, будет известна также только после его прохождения. Следовательно, для прогноза такие значения вообще бесполезны.

Можно рассчитать точность прогнозирования при постоянном использовании некоторой стандартной скорости затухания весовых множителей, например, ? = 0,9. Существуют предпосылки для теоретического обоснования этой величины. Можно также определить точность прогноза при заранее известном оптимальном значении скорости затухания. Различие между ними будет относительно мало по сравнению с тем случаем, когда наилучшее значение скорости затухания весовых множителей для длинного ряда выбирается по данным для коротких отрезков этого ряда (содержащих не менее 50 результатов наблюдений).

Байесовские прогнозы. Гаррисон и Стивенс[223] разработали строгий подход к прогнозированию временных рядов, включающий в виде частных случаев большинство ранее разработанных методов. При таком подходе каждому наблюдению до его проведения ставится в соответствие ряд первичных вероятностных значений коэффициентов модели. Построение модели можно начинать из состояния полной неопределенности. Даже в этом случае предложенный метод позволяет довольно точно устанавливать вероятностные значения коэффициентов.

После того как получены результаты наблюдений, по правилу Байеса определяют апостериорные вероятности, основываясь на которых вычисляют распределение вероятностей прогнозируемой величины. Такой подход позволяет: игнорировать кратковременные изменения прогнозируемой переменной, регистрировать ступенчатые изменения в основном процессе, отслеживать изменения наклона соответствующих кривых.

Многократное повторение приведенной схемы вычислений дает возможность уменьшить число вероятностных распределений до числа состояний изучаемого процесса. В число состояний обычно входят нейтральное состояние, которое характеризуется неизменными значениями всех элементов процесса, и состояния, которые соответствуют различным, возможным значениям каждого коэффициента и помех. В таких состояниях дисперсия распределения намного выше, чем в нейтральном состоянии, что указывает на отклонение того или иного коэффициента модели от нормы. Возможность уменьшения числа состояний весьма существенна, так как в противном случае число распределений возрастало бы пропорционально квадрату числа наблюдений.

Ошибки прогноза. В любом из методов статистического прогнозирования собственно прогноз представляет собой, по существу, оценку ожидаемого распределения результатов наблюдений в будущем. Для того чтобы на основе полученного прогноза можно было принимать решение, в большинстве случаев необходимо знать исходное распределение. Если это распределение описывается стандартной функцией, то, определив один или два его параметра, можно оценить вероятности возможных результатов будущих наблюдений.

Вид распределения вероятностей. Для целей формального анализа часто удобно принимать предположения о том, что помеха (ошибка) в исходных данных подчиняется нормальному закону распределения. Однако это предположение нельзя считать обоснованным для любых реальных наблюдений. Распределение шума нередко асимметрично и может иметь две или большее количество мод. Даже когда распределение симметрично относительно единственной моды, эксцесс плотности распределения может сильно отличаться от 3.

Прогнозируемая выходная переменная характеризуется распределением, дисперсия которого зависит от дисперсии шума в исходных данных. Поскольку прогнозы вычисляются на основе результатов многих наблюдений, входная переменная обычно описывается нормальным законом распределения независимо от того, каков вид распределения, описывающего шум в исходных данных.

Распределение ошибок при прогнозировании зависит как от распределения самой выходной переменной, так и от распределения соответствующего ей шума, который обычно считается не зависящим от шума в исходных данных. При прогнозировании суммы значений переменной интенсивности в течение времени упреждения, которое намного больше интервала между наблюдениями, распределение ошибок представляет собой распределение суммы выборок из нескольких таких распределений и с возрастанием времени упреждения все более и более стремится к нормальному.

Дисперсия ошибок прогноза. В большинстве случаев, представляющих практический интерес, исходное распределение может быть восстановлено из полученного по прогнозу среднего значения и какого-либо другого параметра, характеризующего распределение выходной переменной. В качестве такого параметра выбирается стандартное отклонение.

Обычно прогноз предполагает анализ некоторого набора временных рядов. Для каждого ряда существует определенная зависимость между разбросом ошибок и уровнем прогноза, которые связаны между собой. Например, хотя объемы добычи нефти aw и газа ar, прогнозируемые на данный год, могут сильно отличаться друг от друга, между прогнозами добычи разных видов топлива существует четкая корреляция в соответствии с соотношением ?2 ~ ?a?, где параметры ? и ? представляют собой характеристики всего семейства прогнозов добычи топлива. Этот же результат справедлив и для прогнозов добычи различного сырья. Отсюда следует, что, исходя из всего семейства прогнозов, можно оценивать параметры ? и ?, а затем использовать связывающее их соотношение в целях установления стандартного отклонения распределения ошибок для любых отдельных рядов.

Другое соотношение между величиной a и параметрами ?, ? и ? может иметь вид[224]: ?2 = ?a + ?a2 с анализом процессов, описываемых подобными соотношениями, согласно методологии Stevens С.F. (1974)[225].

Если распределение описывается нормальным законом, то среднее абсолютное отклонение равно 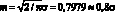. Для других распределений аналогичное соотношение может иметь иной вид. Так как средняя ошибка прогноза должна быть равна нулю, то дисперсия определяется среднеквадратичной ошибкой. Выбрав подходящую модель процесса, можно пересматривать значения коэффициентов этой модели по среднеквадратичной ошибке каждый раз, когда поступает новая информация и заново измеряется ошибка прогноза.

Интересны особенности определения дисперсии ошибок прогноза переменной интенсивности в течение времени упреждения при его периодическом уточнении. Если шум результатов наблюдений автокоррелирован незначительно, то стандартное отклонение, используемое для принятия решений, приблизительно равно . Если имеет место автокорреляция шума, то выражение для стандартного отклонения может быть записано в виде , где ? – дисперсия ошибок прогнозов для отдельных интервалов, ?1 – стандартное отклонение ошибок одного знака, ?L – время упреждения, измеренное в интервалах между проверками прогноза, и ? – постоянная, которая является характеристикой всего семейства прогнозируемых рядов.

Метод следящих сигналов. Точность прогноза зависит от шума входных переменных. При этом разумно считать, что прогнозы не содержат систематической ошибки, так как средняя ошибка прогноза должна быть равна нулю. Пока модель соответствует изучаемому процессу, ошибки прогноза должны колебаться около нуля. Если же модель прогноза ошибочна или станет ошибочной из-за того, что резко изменится сам процесс, то появится последовательность «положительных» или «отрицательных» ошибок и средняя ошибка прогноза больше не будет равна нулю.

Метод следящих сигналов состоит в том, что с помощью ЭВМ систематически осуществляется проверка близости средней ошибки прогноза к нулю. Если средняя ошибка превысит некоторый заранее установленный предел, формируется предупреждение, дающее возможность пользователю принять необходимые меры для своевременной корректировки прогноза. Для осуществления такой корректировки необходимо установить конкретную причину смещения прогноза и затем внести в модель необходимые изменения; принять новые значения для одного или большего количества коэффициентов; изменить некоторые или все весовые множители; наконец, изменить сам вид модели.

В соответствии с одним из научных направлений эта задача должна решаться автоматически с помощью специально создаваемых вычислительных систем, способных заменить труд большого количества людей. В соответствии с другим направлением в решении указанной задачи должны принимать участие специалисты, учитывающие весь комплекс информации, собираемой за длительные промежутки времени. Многие конкретные прогнозы не поддаются автоматическому уточнению. Сократить время отклика запрограммированных решений, позволяющих внести необходимые изменения в прогноз, позволяет постоянное участие специалистов в процессе прогнозирования.

Для обнаружения выбросов следящих сигналов и, соответственно, для выявления недопустимых отклонений средней ошибки прогноза могут быть использованы следующие виды контрольных величин[226].

Кумулятивные суммы. Величина кумулятивной суммы ошибок прогноза задается выражением 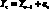. При выполнении равенства Yo = 0 сумма колеблется около нуля, если прогнозы не смещены, и быстро возрастает при появлении последовательности ошибок прогноза одного знака. Для модели, описанной полиномом (n – 1)-й степени при интенсивности затухания весовых множителей ?, дисперсия кумулятивной суммы равна

,

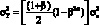где 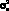– дисперсия ошибок прогноза.

Для анализа выброса может быть использовано соотношение 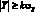. Например, выбросы регистрируются при k = 3. Уменьшить число ложных регистраций можно при значении множителя k > 3. Уменьшить вероятности пропуска фактических изменений ошибок прогноза позволяет множитель k < 3.

Сглаживание ошибки. Простое экспоненциальное сглаживание алгебраической суммы ошибок прогноза в виде 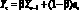создает основу для регистрации выброса, например, в случае выполнения соотношения 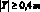. Вместо множителя 0,4 может быть использован и какой-либо другой множитель. При этом среднее абсолютное отклонение m заменяется величиной 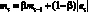. Дисперсия сглаженных ошибок прогноза может быть выражена соотношением .

Такой подход имеет два существенных преимущества по сравнению с предыдущим.

Пусть произошла большая единственная ошибка, но все же не настолько, чтобы вызвать выброс следящего сигнала. При использовании первого метода, начиная с этого момента, величина не взвешенной кумулятивной суммы колебалась бы около уровня, соответствующего этой большой единственной ошибке. При этом, несмотря на вполне допустимые ошибки последующих прогнозов, будут регистрироваться выбросы следящих сигналов. Это во-первых.

Во-вторых, допустим, что следящий сигнал близок к выбросу (кумулятивная сумма близка к одному из пределов) и мы получили идеальный прогноз. При применении первого метода величина не взвешенной кумулятивной суммы не изменится и оценка стандартного отклонения ?e уменьшится. В результате произойдет сжатие области допустимых отклонений и увеличится вероятность регистрации выбросов следящего сигнала. Использование сглаженных ошибок позволяет успешно преодолеть обе указанные трудности.

V-образные маски. Маски подобного типа были разработаны на основе метода последовательного анализа Вальда. V-образная маска помещается вершиной вблизи самого последнего значения (не взвешенной) кумулятивной суммы ошибок прогноза. Ее раскрытая часть обращается в сторону предыдущих членов ряда. Признаком значимого смещения прогнозов является то, что хотя бы одно из предыдущих значений кумулятивной суммы лежит вне маски. Угол наклона и точка пересечения двух прямых, составляющих V-образную форму маски, вычисляются на основе анализа ошибок и вероятностей пропустить значительное отклонение и ошибочно обнаружить какое-то отклонение, когда его на самом деле не было.

Данный метод был обобщен для масок параболической формы[227] при всех возможных уровнях смещения прогноза, которые можно считать существенными. Применение такого подхода к анализу временных рядов позволило успешно прогнозировать предстоящие изменения курса акций на бирже.

Коррекция исходных данных. Внешние воздействия и ошибки, имевшие место при регистрации исходных данных, могут привести к тому, что результаты последующих наблюдений нельзя будет использовать для уточнения прогноза. Если отклонение полученного результата от прогнозируемого значения превышает 4?, то рекомендуется по возможности скорректировать входные переменные и только после этого продолжать прогнозирование на основе выбранной модели.

Уточнение прогноза. Существует много различных методов прогнозирования, которые (при правильном их использовании) должны приводить практически к одному результату – выбору одного и того же варианта из ряда возможных и одинаковой оценке экономических последствий выбранного варианта[228]. Правильное ведение прогнозирования предполагает, в частности, применение соответствующих критериев при пересмотре прогнозов. Известны три вида подходов, широко применяемых для пересмотра и уточнения прогнозов при анализе больших рядов.

Адаптивное сглаживание[229]. Основы метода адаптивного сглаживания были заложены при разработке метода экспоненциального сглаживания и затем развиты путем включения в рассмотрение сезонных моделей. Во многих случаях адаптивное сглаживавшие позволяет получать хорошие результаты в течение короткого промежутка времени. Это иногда более важно, чем получение более точного прогноза в течение длительного времени и с применением значительных усилий.

Математическое описание модели, позволяющей проводить прогнозирование для любых рядов, имеет вид (ранее уже использовалось) 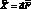, где – вектор m коэффициентов, вычисленных отдельно для каждого временного ряда, – матрица соответствующих функций размерности m??o, строки которой соответствуют каждому из m членов, модели и столбцы – каждому из ?o интервалов прогнозирования. Компоненты вектора представляют собой прогнозируемые значения для каждого из интервалов.

Если в течение годового цикла имеется 12 наблюдений, то основная частота равна ? = 2?/12 и существуют только семь возможных видов моделей. Простейшая модель включает только уровень и тренд, а наиболее сложная содержит также члены рядов Фурье вплоть до cos 6??. Строки матрицы имеют вид:

При других основных частотах возможны и другие модели.

Коэффициенты вычисляются сначала по методу наименьших квадратов в соответствии с N исходными данными (m?N) матрицы . Гармоники включаются в модель вплоть до той частоты, при которой показатель степени (квадрат амплитуды) составляет, по крайней мере, 0,25 от величины дисперсии остатков, получаемых при подгонке этой модели с учетом имеющихся для ошибок степеней свободы.

С каждым следующим наблюдением вектор пересчитывается на новый 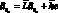, где – матрица перехода (m?m), которая определяется с помощью выражения 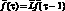и переводит значения соответствующих функций из одного периода времени в следующий. Столбец матрицы , имеющий номер ?, обозначается как f(?). Ошибка (скаляр) самого последнего прогноза, сделанного на один интервал вперед, равна .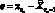

Вектор , характеризующий m постоянных сглаживания, определяется следующим образом. Используя z-преобразования и некоторые элементарные тригонометрические соотношения, можно вывести выражение для матрицы в замкнутом виде: .
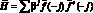Так как ? < 1, то значимость более старых данных снижается и увеличивается вес, приписываемый более поздним данным. Следовательно, вектор сглаживания можно записать как .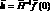

Величины и  необходимо вычислить только один раз, так как при дальнейшем пересмотре прогнозов они не изменяются.

Если прогнозы составляются для переменных интенсивности (например, таких, как на запас топлива) и результаты наблюдений получены в нерегулярные интервалы времени, то исходные данные преобразуются к величинам, характеризующим скорость их изменения на равномерных интервалах времени. Получаемые в результате прогнозы могут быть приведены в соответствие с величиной будущих интервалов времени. Подобное использование сечения какой-либо входной переменной одинаково пригодно для любых рядов и не приводит к такому же увеличению дисперсии, какое имело бы место в случае получения сечения из данных предыстории.

Метод Бокса – Дженкинса[230]. Согласно данному методу, прогнозы составляются на основе всестороннего анализа статистических свойств рядов. Для того чтобы в полной мере использовать его достоинства, требуются длинные ряды (содержащие не менее 100 результатов наблюдений). Это в значительной степени помогает понять изучаемый процесс – получить предварительные данные относительно возможных изменений процесса в будущем. С помощью данного метода может быть проанализирован гораздо более широкий круг моделей, чем с помощью метода адаптивного сглаживания. Он особенно полезен при получении как можно более точного прогноза.

Анализ моделей по методу Бокса – Дженкинса начинается с формирования разностей из исходных данных Z? и вычисления частных автокорреляционных функций ? для разностных рядов 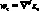. Затем разностные ряды вводятся в модель с соответствующим числом коэффициентов авторегрессии и скользящего среднего:

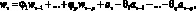
где ?p – частные автокорреляционные функции.

Для оценки коэффициентов в моделях такого типа и вычисления дисперсии шума в результатах наблюдений используются методы наименьших квадратов. Операторы разности скользящего среднего могут быть разложены таким образом, чтобы выразить модель прогнозов через исходные данные наблюдений:

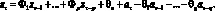
По методу Бокса – Дженкинса сначала прогнозируется изменение преобразованных входных переменных, а затем осуществляется обратное преобразование.

Если необходимо проанализировать сезонные циклы, то вклад от каждого из них вычисляется путем составления разностей для определенных отрезков цикла. Например, для годового цикла в качестве таких отрезков можно принять месяцы, и тогда прогноз для каких-то месяцев в будущем будет основываться на известных данных для этого месяца в прошлые годы.

Одно из основных применений метода Бокса – Дженкинса связано с управлением процессами в химической промышленности, где имеются ряды температур, давлений, скоростей потоков и т.п. с большим числом известных результатов наблюдений и неплохо известна возможная динамика изменения системы, подлежащей управлению. Цель управления состоит в том, чтобы наиболее рациональным образом менять технологические параметры – температуру, давление или скорость потока. Значительные усилия по разработке точных прогнозов для подобных производственных процессов вполне оправдываются достигаемым при этом экономическим эффектом.

Байесовские прогнозы[231]. Байесовские прогнозы включают основные положения предыдущих методик как частные случаи. Пока результаты наблюдений согласуются с прогнозами, последние стабильны и ожидаемое распределение ошибок прогнозов ограничено узкими пределами в соответствии с шумом в результатах наблюдений. Появление хотя бы одного большого отклонения повышает чувствительность метода. Если последующие наблюдения подтверждают скачкообразное или постепенное изменение изучаемого процесса, прогнозы быстро корректируются с помощью новой модели. Однако, если указанное отклонение представляло собой случайный выброс, прогноз остается без изменения.

Объем вычислений при использовании рассматриваемого метода гораздо больше, чем при адаптивном сглаживании, так как успешное прогнозирование гарантируется и в тех случаях, когда могут возникнуть непредвиденные и существенные изменения в прогнозируемом процессе. Начать прогнозирование можно, если есть предварительные сведения об ожидаемых событиях, при весьма скромных данных или вообще при их отсутствии. Большой объем результатов наблюдений позволяет начать прогнозирование при отсутствии исходных предпосылок о поведении прогнозируемой величины. Применяемый алгоритм вычислений позволяет построить модель процесса по данным его предыстории.

Типичная модель для результатов текущих наблюдений может быть представлена выражением d? = ?? + ??, где ? – уровень полезной составляющей и ? – шум текущего наблюдения. Текущий уровень связан с трендом выражением ?? = ?? – 1 + ?? + ??, где тренд изменяется по закону ?? = ?? – 1 + ??. Скачкообразное изменение основного уровня ?, изменение тангенса угла наклона кривой ?, описывающей зависимость выходной переменной от времени, а также шум ? считаются независимыми переменными. Предполагается, что они распределены по нормальным законам с нулевым средним и известной, но не обязательно постоянной дисперсией V?, V?, V?,.

В модели, которая описывает много состояний, обычно имеются два состояния для каждого возможного возмущения, которое характеризуется своим значением дисперсии Vj. В устойчивом состоянии дисперсия мала. В состоянии изменения дисперсия велика. Имеются также априорные вероятности ?j того, что состояние j не изменяется.

7. Возможности комбинированного подхода

Сравнительная оценка. Совершенствование эвристического метода ведется не на уровне его внутренней структуры, а на уровне внешнего оформления: подбора соответствующих по квалификации и количеству экспертов, создания благоприятных условий для проведения оценок, обработки результатов опроса и т.п.

Он принципиально применим для прогнозирования любых процессов, независимо от того, непрерывный процесс или дискретный, стационарный или нестационарный, имеется ли скачок, требуется качественный или количественный прогноз, имеется статистика или не имеется, описаны ли математически закономерности процесса или нет. Однако метод является субъективным и он пригоден только тогда, когда существуют эксперты, знакомые с прогнозируемой ситуацией. В этом его основные ограничения, которые частично сглаживаются при групповой экспертизе. Это, по-видимому, и привело к потребности перехода к математическим методам.

Классический статистический метод (метод наименьших квадратов): идеален с позиций объективности, не требует знания физических закономерностей, применим как для непрерывных, так и для дискретных процессов. Он одинаково пригоден как для стационарных, так и для нестационарных процессов. Для его успешного применения требуется достаточно большое число статистических данных на участке наблюдения, без которых метод дает существенные погрешности, и функция, описывающая процесс. Метод относится с одинаковым доверием к информации как в начале участка наблюдения, так и в конце его. В этом – его слабое место: невозможно предсказать результаты скачка (изменения характера процесса) не только на участке упреждения, но и на участке наблюдения.

Стремление улучшить статистическое прогнозирование привело к созданию методов весовых множителей, когда возможен учет изменения характера процесса, если оно началось на участке наблюдения. Если же оно началось на участке упреждения, то использование методов проблематично. Варьируя степень важности статистических данных на том или ином участке наблюдения, можно обучать модель прогнозирования. Отсюда, вероятно, возможен переход к методам, построенным на идеях распознавания образов, хотя в методическом плане это остается пока не до конца разработанной идеей.

Методы, основанные на принципе наименьших квадратов, предназначены для обработки дискретных статистических данных. Существуют также алгоритмы прогнозирования, предназначенные для обработки непрерывных статистических данных. Они рассчитаны на применение в автоматических системах управления, прежде всего в системах автоматического регулирования. Например, метод следящих сигналов или оптимальных фильтров.

Первоначально фильтры использовались для прогнозирования стационарных процессов (фильтр Винера – Хопфа), а затем и для прогнозирования нестационарных процессов (фильтр Калмана). Принципиальных трудностей применения этих фильтров для прогнозирования дискретных процессов не имеется, если есть достаточно представительные статистические данные. Фильтры могут быть обучаемыми. Одна из идей такого «обучения» предполагает: уточнение по мере накопления статистических данных корреляционной функции процесса, вычисление параметров нового оптимального фильтра, последующую перестройку фильтра.

Наибольшим злом для классических фильтров являются скачки на участке упреждения и необходимость знания корреляционной функции процесса.

Использование для прогнозирования канонических разложений случайных функций – метод по своему принципу промежуточный между методом наименьших квадратов и использованием фильтров.

Итак, общее достоинство статистических методов – объективность, недостаток – непредсказуемость скачков на участке упреждения. Применение того или иного из них зависит от технологии прогнозирования, формы статистических данных, периодичности выдачи прогноза.

Прогнозирование с помощью моделирования процессов развития (причинно-следственное прогнозирование) является наиболее целесообразным в том случае, если имеется корректное математическое описание процесса и если он детерминирован. Во всяком случае, стохастическая часть процесса не является определяющей, и речь идет о детерминированном хаосе. Процессы стохастические по своему характеру плохо поддаются математическому моделированию.

Часто удается построить модель, в которой есть неизвестные коэффициенты или функции. Даже такие модели оказываются полезными при дальнейшем прогнозировании статистическими методами. Они позволяют выявить: характер детерминированной основы процесса и области возможных изменений характера процесса.

Совместная обработка. Как отмечалось, математическое прогнозирование часто включает в себя некоторые эвристические элементы: участие экспертов в процессе выработки математической модели прогнозируемого процесса и логический анализ результатов прогнозирования.

Комплексное использование результатов математического и эвристического прогнозирования предполагает использование самостоятельной методики прогнозирования. Такая методика позволяет после опроса высококвалифицированных специалистов, не принимавших участия в математическом прогнозировании, получить данные о прогнозируемом объекте независимо от результатов математического прогнозирования.

Задачу комплексного использования результатов эвристического и математического прогнозирования можно поставить следующим образом. Имеем данные прогнозирования количественных характеристик исследуемого процесса, полученные независимо с помощью экспертов и в результате математического прогнозирования. Требуется их обобщить.

Для решения поставленной задачи прежде всего необходимо сравнить полученные данные. Если эти данные «не противоречат» друг другу, их следует совместно обработать, в результате чего должен быть получен комбинированный прогноз. В противном случае необходимо провести анализ причин, вызвавших противоречивые результаты: пересмотреть экспертами некоторые исходные предпосылки при ознакомлении с результатами математического прогноза, видоизменить математическую модель процесса, провести повторный анализ и проверку исходных данных. После этого выполнить повторное прогнозирование.

Для определения понятий противоречивости и непротиворечивости данных, оценим, какие данные используются при сравнении результатов. Как отмечалось, в результате математического прогнозирования мы имеем точечный прогноз 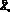и интервальный прогноз 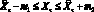при данном уровне вероятности p. Во многих случаях распределение ошибок прогноза является симметричным: m1 = m2 = 1/2m, где m характеризует размер области, куда с вероятностью p попадает будущее значение прогнозируемого процесса при времени упреждения.

Очевидно, для того чтобы можно было сравнивать результаты эвристического и математического прогнозирования, первые следует представить в аналогичном виде.

Оценки экспертов могут иметь следующий вид. Прежде всего, можно получить оценку наиболее вероятного значения прогнозируемой величины. Часто принимается нормальный закон распределения точечных оценок группы экспертов. Таким образом, мы будем иметь точечный экспертный прогноз и его дисперсию ??.

Другим видом экспертных оценок могут быть возможные границы прогнозируемой величины. Именно такую информацию эксперты дают наиболее охотно. Для проведения дальнейшего анализа необходимо априорное принятие вида закона распределения прогнозируемой величины между крайними оценками, даваемыми экспертами. В качестве таких законов, например, могут быть, приняты следующие[232]: частный случай ?-распределения, логарифмически нормальное распределение, равновероятное распределение. Различные авторы рекомендуют, кроме указанных, еще и другие виды распределений (гамма-распределение, распределение Вейбулла и т.д.). Можно пользоваться, например, самым простым по форме распределением – равновероятным.

В результате сформируются точечный и интервальный (при данной вероятности p) экспертные прогнозы. Заметим, что суммарная оценка результатов экспертного опроса могла бы определяться не как средняя арифметическая, а с учетом индивидуальных «весовых» показателей экспертов. Однако введение «весовых» показателей экспертов встречают серьезные практические трудности как из-за известного произвола в их определении, так и вследствие невозможности сохранения тайны при их использовании и неизбежно возникающих при этом обид.

Реже встречается случай, когда эксперты дают три оценки: максимальное значение прогнозируемой величины, минимальное и наиболее вероятное. В этом случае можно получить суммарную плотность распределения и определить прогноз и его дисперсию ??.

Таким образом, в результате экспертного опроса и обработки результатов можно иметь точечный 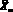и интервальный 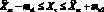экспертные прогнозы при данном уровне вероятности p.

Теперь не трудно определить понятия противоречивости и непротиворечивости результатов эвристического и математического прогнозирования. Сравним точечные и интервальные прогнозы. Точечные прогнозы совпадать не могут. Вероятность такого события равна нулю. На практике могут встретиться следующие три случая.

Случай 1. Доверительные интервалы одного прогноза охватывают доверительные интервалы другого. Их общая область равна области, определяемой доверительными интервалами охватываемого прогноза mo.

Случай 2. Доверительные интервалы частично перекрываются.

Случай 3. Доверительные интервалы не имеют общей области mo = 0.

Например, может быть принято следующее решающее правило, определяющее противоречивость или непротиворечивость результатов комплексного прогнозирования. Результаты прогнозирования не противоречат друг другу, если точечные прогнозы принадлежат общему доверительному интервалу , и величина общей области mo такова, что mo/mmin ? k . В противном случае результаты прогнозирования являются противоречивыми.

Вероятность p, на основе которой определяется доверительный интервал, является входной величиной и поэтому определяется вне системы прогнозирования.

При симметричном распределении прогнозов (как эвристического, так и математического) и соблюдении первого условия при k = 0,5 второе условие будет выполняться всегда. Если исследователя удовлетворяет то, что общая область mo будет не меньше половины области с меньшими доверительными интервалами, то можно ограничиться для принятия решения о противоречивости результатов прогноза только первым условием. В случае несимметричного распределения прогнозов величину k следует определять на основании опыта совместного исследования эвристических и математических прогнозов. Во многих случаях результаты математического прогнозирования могут считаться распределенными симметрично. Что касается эвристического прогнозирования, то суммарный результат прогнозирования (по опросу N экспертов) также во многих случаях можно считать имеющим симметричное распределение.

Если результаты эвристического и математического прогнозирования являются непротиворечивыми (в указанном выше смысле), возникает задача их совместной обработки для получения комбинированного прогноза. Одним из возможных методов получения комбинированного точечного прогноза является нахождение величины 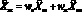, где wэ
и wм – соответственно веса эвристического и математического прогноза, равные, соответственно,

Очевидно, wэ + wм = 1. Такое принятие веса прогноза позволяет ослабить влияние на конечный результат (комбинированный прогноз) прогноза, имеющего слишком большую дисперсию.

Для решения вопроса о том, можно ли считать результаты, полученные двумя методами, совпадающими (непротиворечивыми), возможно использовать и другой метод.

Если полагать обе оценки распределенными по нормальному закону и обозначить оценки их математических ожиданий и , среднеквадратические отклонения ?э и ?м, то по величине 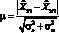можно определить вероятность того, что обе выборки принадлежат к одной и той же генеральной совокупности. Задавшись уровнем этой вероятности, можно ответить на вопрос о том, противоречивы две оценки или нет.

Логический анализ и особенности. Логический анализ проводится тогда, когда результаты, полученные двумя различными методами прогнозирования, противоречивы. Он может быть проведен эвристическим или математическими методами.

При логическом анализе широко используется метод аналогий, который обычно предполагает сравнение близких по физическим свойствам процессов, с теми же процессами, но протекающими в других условиях (например, сравнение нашего опыта с зарубежным); расчленение процесса на составные части и их анализ; выделение составных частей из более сложного процесса; сравнение с процессами, протекающими параллельно; учет взаимных связей с параллельными процессами и т.д.

Логический анализ позволяет ответить на вопросы, которые могут оказаться решающими при оценке результатов того или иного метода прогнозирования.

Во-первых, удается установить возможные пределы изменения тех или иных величин. Например, из анализа газодинамических зависимостей, описывающих движение пороховых газов в пространстве каморы, можно установить предельную скорость артиллерийского снаряда, выстреливаемого из ствола. Из анализа характеристики всех химических элементов можно установить предельные калорийности химического топлива. Таких примеров можно привести немало. Важно, что получив такую оценку, удается оценить тот или иной прогноз.

Во-вторых, полезными могут оказаться сведения, которые часто без особого труда можно получить простым сопоставлением (например, «некоторая величина заведомо больше нуля» или «заведомо больше (меньше) некоторой другой величины»).

В-третьих, в отдельных случаях имеется возможность предсказать также тенденции развития. Так, анализ развития железнодорожного транспорта предсказывает направления развития разных видов этого транспорта (электровозов, тепловозов, паровозов). Очевидно, что количество электровозов будет возрастать быстрее, чем тепловозов, а количество паровозов будет убывать. При этом в ряде случаев удается получить не только первую производную (если не величину, то хотя бы ее знак), но и вторую производную (опять-таки ее знак), то есть оценить, будет ли увеличиваться скорость возрастания (убывания) или она будет уменьшаться.

В-четвертых, иногда можно установить то, что один процесс будет превуалировать (мажорировать) над другим. Независимое прогнозирование характеристик каждого из двух процессов, сравнение их результатов и корректировка могут существенно повысить точность прогнозирования (во всяком случае, устранить грубые ошибки).

В-пятых, особенно велика роль логического анализа в прогнозировании возможных скачков. С его помощью можно предвидеть начало реализации некоторой новой технической идеи и ее последствия: прекращение производства технических устройств старого типа и развертывание производства нового.

В-шестых, предполагается построение дерева целей, достижение которых необходимо для реализации прогнозируемого события, и последующее изучение этого дерева. Возможны три конечные цели исследования.

Прогнозируется срок совершения некоторого события. Построив дерево целей, оценивают сроки реализации событий на каждой ветви (в лучшем случае минимальный и максимальный). Затем методами сетевого планирования определяют итоговый срок (его максимальное и минимальное значения). Здесь характерны две особенности: комбинация эвристических и математических методов и применение косвенного прогнозирования, то есть изучение частных процессов и определение на их основе итогового результирующего процесса.

Прогнозируется сам факт совершения некоторого события. Тогда ветвям дерева приписываются оценки: нуль или единица. Непосредственный анализ дерева целей проводится с помощью аппарата математической логики.

Возможен случай, когда прогнозируется вероятность осуществления данного события в заданный срок. Тогда каждой ветви дерева целей приписывается вероятность осуществления в заданный срок. Он, как правило, не совпадает с общим сроком и определяется исходя из дерева сроков. Затем производится анализ дерева вероятностей, например, с использованием теории марковских процессов.

В простейшем случае имеется одна последовательная цепочка следующих друг за другом I событий с вероятностью pi. Вероятность итогового события Если две цепочки параллельны и вероятности на них p1 и p2, то вероятность итогового события P = p1(1 – p2) + p2(1 – p1).

Реально встречающиеся деревья представляют собой комбинации параллельных и последовательных цепочек. Вероятность итогового события определяется на основании приведенных соотношений с учетом реальной структуры дерева.

В-седьмых, при логическом анализе можно широко использовать различные полуэмпирические, эмпирические зависимости, которые можно называть эвристическими.

Общие рекомендации по комбинированному прогнозированию выглядят следующим образом.

Выбор комбинированного метода в значительной степени зависит от срока, на который производится прогноз, то есть от величины участка упреждения и от объема имеющейся в распоряжении исследователя информации. Например, производится прогноз объема производства или развития науки и техники на короткий срок (один-два года). При наличии достаточной статистической информации лучшим методом будет статистический. В случае более длительных прогнозов (5–7 лет) возникает опасность появления скачков на участке упреждения, и использование только статистических методов является опасным. Их следует подкреплять либо логическим анализом, либо моделированием процессов развития, либо эвристическими прогнозами.

Наиболее сложно обстоит дело при долгосрочных прогнозах (15–20 лет). В этом случае, единственно надежным методом является комбинированный, который предполагает следующую последовательность действий.

На основе анализа причинно-следственных моделей определяется вид детерминированной основы процесса (вид функционала). В полученном функционале могут (и должны) быть неизвестные коэффициенты, а иногда и функции. Неизвестные коэффициенты (функции) вычисляются с помощью статистических методов. Вид последних выбирается в зависимости от вида статистических данных, имеющихся в распоряжении исследователя. Так получается математический прогноз.

Независимо от полученных результатов осуществляется прогнозирование эвристическим методом. Затем два полученных прогноза сравниваются. Это сравнение производится как статистическим методом, так и с использованием метода логического анализа. В случае непротиворечивости прогнозов проводится их совместная обработка. Полученный обобщенный прогноз обладает более высокой точностью, чем два предыдущих, взятых раздельно. В случае, когда «прогнозы» противоречивы, методом логического анализа устанавливается несостоятельность одного из них.

При несостоятельности статистического прогноза меняется модель прогнозирования. В случае наличия скачка или неправомерного использования статистических данных они вообще исключаются из рассмотрения. Эвристическое прогнозирование можно повторить либо с обсуждением полученных результатов прежними экспертами, либо с привлечением новых экспертов.

Возможны и другие варианты комбинированного прогнозирования. Например, использование нескольких статистических методов, исключение эвристического метода или метода моделирования. Однако во всех случаях следует помнить, что прогнозирование – слишком сложный процесс для того, чтобы упустить малейшую возможность уточнения прогноза.

Контрольные вопросы по лекции 24:

1. Что такое прогнозирование?

2. Поясните общую схему прогнозирования.

3. Сформулируйте основные подходы к решению вопросов прогнозирования.

4. Что такое эвристическое прогнозирование?

5. Что такое математическое прогнозирование?

6. В чём полезность комбинированного прогнозирования?

7. Надо ли учитывать психологические аспекты восприятия нового?

8. Что такое система сглаживающих весовых множителей?

9. Поясните метод следящих сигналов.

10. В чём существо методов уточнения прогнозов?

11. Объясните метод Бокса-Дженкинса.

12. В чём основополагаемость Байесовских прогнозов?

13. Какова идея организации совместной обработки результатов эвристического и математического прогнозирования?